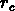 (c'est à dire une distance
minimale au centre du champ) dans lequel il n'est pas possible
de déplacer tous les bras sans collisions:
(c'est à dire une distance
minimale au centre du champ) dans lequel il n'est pas possible
de déplacer tous les bras sans collisions:
L'une des propriétés les plus intéressantes de MEFOS est donc la possibilité d'attribuer automatiquement les fibres aux objets (et de préparer les attributions avant les observations) et de voir le champ autour de chaque objet, permettant ainsi une correction du positionnement du bras. Il y a des cas dans lesquels on veut observer des objets particuliers. Une attribution ``manuelle" des bras reste donc nécessaire. Mais dans d'autres situations, comme dans le cas d'un grand relevé de galaxies, c'est la statistique qui nous intéresse, et non les objets individuels. Dans ce cas, le mode d'attribution automatique est particulièrement approprié. Il faut cependant souligner qu'une telle sélection automatique, en fonction de l'algorithme utilisé, peut introduire un biais dans la sélection des objets. Il est important de considérer cet effet, surtout là où l'on a intérêt à étudier la distribution des objets.
En principe, si l'on a N bras rectangulaires de largeur l,
qui peuvent se déplacer seulement suivant la direction radiale,
il existe un rayon limite 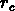 (c'est à dire une distance
minimale au centre du champ) dans lequel il n'est pas possible
de déplacer tous les bras sans collisions:
(c'est à dire une distance
minimale au centre du champ) dans lequel il n'est pas possible
de déplacer tous les bras sans collisions:

Pour des distances au centre supérieures à ce rayon, les collisions
seraient impossibles, et la gestion du système serait très simple,
mais le champ ne serait couvert que partiellement. Si l'on se déplace
dans la région du champ qui se trouve à une distance du centre
inférieure à ce rayon 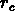 , on peut placer au maximum la
moitié des bras
, on peut placer au maximum la
moitié des bras 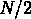 , et cela jusqu'à un rayon
, et cela jusqu'à un rayon 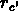 où
les
où
les 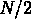 bras entrent à nouveau en collision.
bras entrent à nouveau en collision.
Il est évident que si les bras ne peuvent se déplacer que radialement,
ils ne pourraient couvrir qu'une partie limitée du champ.
Les bras doivent donc avoir une certaine liberté de rotation
(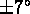 dans le cas de MEFOS ). Ce fait complique le contrôle des bras.
En plus, la caméra à l'extremité de la fibre image,
qui visualise le champ de chaque bras, est située derrière
la fibre objet; donc la visualisation du champ peut donner une situation
de collision, même quand l'observation des objets avec deux bras est
possible; et le programme doit tenir compte de cette possibilité.
dans le cas de MEFOS ). Ce fait complique le contrôle des bras.
En plus, la caméra à l'extremité de la fibre image,
qui visualise le champ de chaque bras, est située derrière
la fibre objet; donc la visualisation du champ peut donner une situation
de collision, même quand l'observation des objets avec deux bras est
possible; et le programme doit tenir compte de cette possibilité.
Il est naturellement impensable de vérifier l'une après l'autre toutes les configurations possibles, même si le programme d'attribution est utilisé avant l'observation. Ainsi la sélection automatique, couplée avec les limites imposés par la mécanique et les collisions, force à l'utilisation d'un algorithme particulier, comme illustré dans le cas de MEFOS .
Le programme d'anticollision pour MEFOS a été developpé par Andrée Fernandez à l'Observatoire de Meudon, il est écrit en langage C++, et fonctionne sur un micro-ordinateur PC-IBM.
Le problème d'attribution des 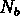 bras à
bras à 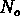 objets peut être
résous dans le cadre du General Assignement Problem,
en appliquant un algorithme dénommé la méthode
hongroise.
Le GAP peut être formulé dans cette forme générale:
supposons qu'il y ait n candidats (i=1,...,n) à n positions
(j=1,...,n) et qu'il soit donnée
une matrice d'évaluation
objets peut être
résous dans le cadre du General Assignement Problem,
en appliquant un algorithme dénommé la méthode
hongroise.
Le GAP peut être formulé dans cette forme générale:
supposons qu'il y ait n candidats (i=1,...,n) à n positions
(j=1,...,n) et qu'il soit donnée
une matrice d'évaluation 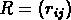 où
où 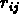 sont des
entiers positifs, pour toutes les i et j.
Une attribution est définie comme le choix
d'un position
sont des
entiers positifs, pour toutes les i et j.
Une attribution est définie comme le choix
d'un position 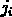 pour chaque candidat
i de manière qu'il n'y ait pas
de position assignée à deux candidats différents.
pour chaque candidat
i de manière qu'il n'y ait pas
de position assignée à deux candidats différents.
Ainsi tous les postes sont attribués et une attribution est une permutation des entiers 1,2,...,n. Le GAP demande: pour quelles attributions la somme des évaluations

est-elle la plus grande?
Le problème dual considère des budgets ``convenables", c'est à dire
des attributions d'une quantité entière non-negative
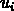 à chaque individu et
à chaque individu et 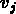 à chaque poste de telle manière
que la somme des attributions au l'individu i et au poste j ne soit
pas inférieure à son évaluation dans ce poste:
à chaque poste de telle manière
que la somme des attributions au l'individu i et au poste j ne soit
pas inférieure à son évaluation dans ce poste:
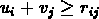
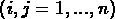 .
La question du problème dual au GAP est alors:
quelle est l'attribution totale
.
La question du problème dual au GAP est alors:
quelle est l'attribution totale
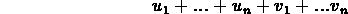
la plus petite possible pour un budget convenable?
Dans notre cas, la solution de ce problème, adapté à notre situation, nous permet d'attribuer de manière optimale n bras à n objets. A la place des évaluations, on a des distances entre les origines des bras (comme origine d'un bras on prende son centre de rotation) et les positions des objets. Nous pouvons distinguer deux problèmes principaux:
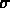 sur 1,...n telle que les
segments ne s'intersectent pas deux à deux;
sur 1,...n telle que les
segments ne s'intersectent pas deux à deux;
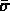 telle que
telle que
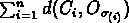 est minimale pour
est minimale pour 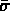 (optimisation).
(optimisation).
Une solution du problème d'optimisation 2 est une solution du problème géométrique 1, et comme conséquence il y a toujours une solution au problème 1.
Le problème 2 est équivalent au programme linéaire dual:
maximiser 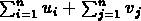 , sous la contrainte
, sous la contrainte
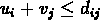
 i,j, où
i,j, où 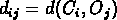 .
Un ensemble d'entiers non-négatifs qui satisfait cette condition est appelé
une couverture, et
.
Un ensemble d'entiers non-négatifs qui satisfait cette condition est appelé
une couverture, et
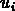 et
et 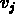 sont quantités à soustraire
respectivement des lignes et des colonnes
de la matrice des distances
sont quantités à soustraire
respectivement des lignes et des colonnes
de la matrice des distances 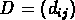 .
.
L'algorithme hongrois consiste à créer un ensemble de zéros indépendants
dans la matrice 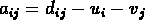 , où l'on initialise
, où l'on initialise
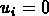 et
et 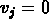 pour tout i, j
(Kuhn, 1955; Tournassoud et Vaillant, 1990); en deux pas il permet
de trouver une solution optimale.
Mais jusqu'ici nous n'avons pas consideré le problème des limites
mécaniques, qui ne rendent pas possibles des attributions
bras-objets pourtant possibles pour l'algorithme décrit ci-dessus
(les bras ne peuvent pas tourner d'un angle supérieur à un certain limite,
et les bras ont une largeur donnée, qui impose une distance minimale
entre bras à ne pas dépasser).
pour tout i, j
(Kuhn, 1955; Tournassoud et Vaillant, 1990); en deux pas il permet
de trouver une solution optimale.
Mais jusqu'ici nous n'avons pas consideré le problème des limites
mécaniques, qui ne rendent pas possibles des attributions
bras-objets pourtant possibles pour l'algorithme décrit ci-dessus
(les bras ne peuvent pas tourner d'un angle supérieur à un certain limite,
et les bras ont une largeur donnée, qui impose une distance minimale
entre bras à ne pas dépasser).
Pour ne pas perdre trop de temps de calcul à la recherche d'une solution
optimale que doit tenir compte de toutes les contraintes,
Tournassoud et Vaillant ont suggeré une approche
heuristique, qui est la suivante:
il faut chercher la permutation qui minimise
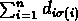 où
où 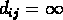 si le couple
bras-objet qui est consideré ne satisfait pas les contraintes mécaniques.
Cette solution, évidemment, n'est pas optimale. Mais elle est sans
doute convenable du point de vue de l'optimisation du temps d'attribution.
Il est ensuite toujours possible de faire des corrections avec des reattributions
manuelles des bras.
si le couple
bras-objet qui est consideré ne satisfait pas les contraintes mécaniques.
Cette solution, évidemment, n'est pas optimale. Mais elle est sans
doute convenable du point de vue de l'optimisation du temps d'attribution.
Il est ensuite toujours possible de faire des corrections avec des reattributions
manuelles des bras.