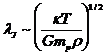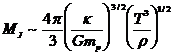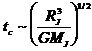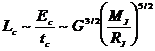La massa di Jeans
Annibale D’Ercole

Abbiamo visto nel livello base che la presenza di onde sonore in un gas diffuso su distanze astronomiche può dare origine alla formazione di strutture con dimensioni dell’ordine della lunghezza d’onda dell’oscillazione. Per capire sotto quali condizioni si verifica un simile evento, consideriamo l’energia termica E_t e gravitazionale E_g di una massa M di gas a temperatura T che per semplicità assumiamo di forma sferica e con raggio R. Trascurando i coefficienti numerici dell’ordine dell’unità, otteniamo:

, (1)

. (2)

La costante C_v che compare nell’equazione (1) rappresenta il calore specifico a volume costante, mentre la costante G presente nell’equazione (2) è la costante gravitazionale; inoltre, nelle due equazioni abbiamo scritto la massa della nube in funzione della sua densità e del raggio R. Da queste equazioni si vede che E_t µ R³ e E_g µ R⁵, e dunque l’energia gravitazionale cresce con il raggio più rapidamente dell’energia termica (Fig. 3). Pertanto, in perturbazioni di piccola lunghezza d’onda l’energia termica prevale su quella gravitazionale causando una nuova espansione del gas compresso.

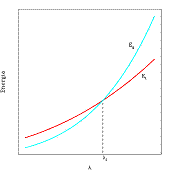
Fig. 3. Energia termica e gravitazionale di una massa di gas la cui estensione è pari alla lunghezza d’onda della perturbazione che la investe. Per perturbazioni con lunghezza d’onda particolarmente grande E_g prevale su E_t, e la massa di gas si isola dando luogo ad una struttura a sé stante. Il punto in cui le due energie si incrociano determina il valore della lunghezza di Jeans, ovvero la dimensione minima per formare strutture.

Le perturbazioni di grande lunghezza d’onda, invece, coinvolgono grandi agglomerati di gas la cui energia gravitazionale è superiore a quella termica; pertanto questi agglomerati non si riespandono una volta compressi, ma continuano a contrarsi fino a “staccarsi” dal gas diffuso formando una struttura isolata. La lunghezza d’onda minima in grado di generare strutture è dunque pari al raggio che si ottiene uguagliando l’equazione (1) all’equazione (2). Con qualche semplice passaggio abbiamo

; (3)

nel ricavare questa formula, abbiamo posto, com’è noto dalla termodinamica, , dove è la costante di Boltzmann e m_p la massa del protone. è detta “lunghezza di Jeans”, e rappresenta dunque il raggio minimo necessario perché una nube di densità e temperatura T collassi. Il criterio di Jeans può anche essere espresso in termini di massa, definendo la “massa di Jeans” come la minima massa che una nube deve avere per poter collassare. Tenendo conto dell’equazione (3) si ottiene:

. (4)

All’interno delle nubi molecolari giganti che si osservano nel disco della nostra Galassia abbiamo tipicamente T = 150 K e g cm^-3. Dall’equazione (4) ricaviamo M_J ~ 13 M_¤, assai minore della massa di questi oggetti che può arrivare a 1000 M_¤. Sembrerebbe allora che sia possibile la formazione di stelle assai massicce, al limite con masse dell’ordine di quella dell’intera nube molecolare. Tuttavia, le osservazioni ci dicono che questo non succede. Si nota inoltre che le stelle si formano in via preferenziale in gruppi, da stelle binarie fino ad ammassi di centinaia di migliaia di membri. Tutto questo può essere compreso mediante il processo di frammentazione gerarchica connesso al criterio di Jeans. Nel livello base abbiamo visto che tale processo si innesca e procede fintanto che il gas rimane trasparente alla radiazione. Una volta che il gas diventa opaco a causa dell’accresciuta densità dovuta al collasso, il processo di frammentazione si ferma, e la massa dei frammenti finali è proprio dell’ordine di quella stellare.

È istruttivo approfondire quest’ultimo punto. Le perdite radiative avvengono, in ultima analisi, a spese dell’energia gravitazionale della nube; l’energia potenziale degli strati di gas in caduta viene trasformata in energia cinetica degli atomi che aumentano la loro velocità e urtano tra loro producendo salti orbitali degli elettroni che, successivamente, ricadendo nelle orbite usuali, emettono radiazione. In conclusione, l’energia a disposizione che può essere emessa da una nube sferica che soddisfi la condizione di Jeans durante il collasso è approssimativamente

.

Quest’energia viene irraggiata in un intervallo di tempo t_c pari alla durata del collasso; dal momento che questo avviene senza sostanziali impedimenti dovuti alla pressione, il tempo di collasso è dato dal tempo di caduta libera. Un elemento di fluido posto alla superficie della nube, ad una distanza R_J dal centro, è sottoposto ad un’accelerazione g = GM_J / R_J²; se questa accelerazione fosse costante, la relazione tra spazio percorso e tempo impiegato a percorrerlo sarebbe, com’è noto, R_J = 0.5gt_c². Il raggio decresce progressivamente e, dunque, in verità, l’accelerazione non è costante, ma possiamo in prima approssimazione considerarla tale per ottenere una valutazione dell’ordine di grandezza del tempo di collasso. Ribaltando la precedente relazione ricaviamo allora

.

La luminosità della nube, ovvero l’energia emessa nell’unità di tempo durante il collasso, diventa pertanto

.

Come abbiamo ricordato più sopra, col procedere del collasso il gas diventa opaco e i fotoni urtano incessantemente con gli atomi. Questa continua interazione porta ad una ben definita ripartizione energetica tra materia e radiazione. Un corpo in cui si realizzi perfettamente tale ripartizione viene detto “corpo nero” e, come sappiamo dalla termodinamica, ogni centimetro quadrato della sua superficie emette una luminosità pari a , dove è la costante di Stefan-Boltzmann; come si vede, questo irraggiamento ha carattere universale perché dipende solo dalla temperatura del corpo e non da altre caratteristiche come, ad esempio, la sua composizione chimica. Tornando ai nostri frammenti opachi, essi tendono ad irraggiare alla loro superficie come un corpo nero, con una luminosità pari a

.

Nello scrivere questa formula, abbiamo tenuto conto del fatto che l’ipotesi di corpo nero è un’idealizzazione e che pertanto la luminosità reale è una frazione < 1 di quella di corpo nero. Ponendo e, dopo un poco di algebra, si ottiene

.

A questo punto, con l’aiuto delle equazioni (3) e (4), otteniamo la massa minima M_J,min acquisita dagli oggetti al termine del processo di frammentazione:

M_¤.

Ponendo ragionevolmente ~ 0,1 e T ~ 1000 K al tempo in cui il gas diventa opaco, otteniamo M_J,min ~ 0,5 M_¤. La frammentazione, dunque, cessa quando si giunge ad oggetti con massa paragonabile a quella stellare. Questo risultato è in accordo con le osservazioni ed inoltre è poco sensibile a un diverso, ragionevole valore di e T.

Nell’ottenere questo risultato abbiamo introdotto parecchie approssimazioni. Ad esempio, abbiamo applicato il criterio di Jeans a frammenti nello stadio intermedio del collasso; questo in principio non è corretto perché il criterio si applica ad un fluido esteso e a riposo. Abbiamo altresì trascurato la rotazione, i campi magnetici e i dettagli del trasporto della radiazione attraverso il gas. Nonostante tutto questo, abbiamo ottenuto risultati ragionevoli.

Il criterio di Jeans si rivela dunque uno strumento semplice ma straordinariamente efficace per una comprensione preliminare di complessi fenomeni fisici.

---

Home Spigolature

Livello Base