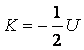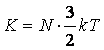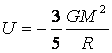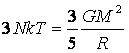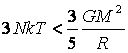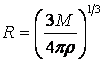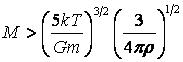Percorsi evolutivi
Claudio Elidoro

Poiché è impensabile riuscire ad approfondire in questa sede tutti i processi che sono stati illustrati nel livello base, ci limitiamo a ragionare un po’ più dettagliatamente solo su uno di essi. Seguendo un rigoroso ordine cronologico, dunque, scegliamo di guardare più da vicino il fenomeno della rottura dell’equilibrio di una nube di gas, cioè quel processo che potrà sfociare nella nascita di una stella.

Per fare questo, partiamo dal teorema del viriale, una legge fisica che afferma come, su tempi lunghi, l’energia cinetica (K) e l’energia potenziale (U) in un sistema in equilibrio sono legate dalla seguente relazione:

(1)

Nel caso della nube di gas che stiamo considerando, è ovvio concludere che l’energia cinetica sia dovuta al moto degli atomi che la compongono, dunque alla loro agitazione termica. Pertanto, indicando con N il numero di tali atomi, possiamo scrivere che:

(2)

dove k è la costante di Boltzmann e T la temperatura del gas.

Ricordando che l’energia potenziale gravitazionale può essere espressa dalla relazione

(3)

riscriviamo l’equazione (1) sostituendo entrambi i termini con le relazioni (2) e (3) appena descritte. Otteniamo in tal modo l’espressione

(4)

che esprime la situazione di equilibrio della nube. Uno sbilanciamento dei due termini decreta ovviamente la cessazione di tale equilibrio. Vale a dire: se il termine a sinistra (energia cinetica) è il maggiore, allora assisteremo a una espansione della nube, mentre se è il termine di destra (energia gravitazionale) il maggiore, allora la nube inizierà a collassare.

Se dunque vogliamo che in una nube si inneschi il meccanismo che sfocerà nella nascita di una stella, dovrà verificarsi che:

(5)

Se ora proviamo a esprimere la condizione (5) sostituendo a N il rapporto M/m (cioè il rapporto tra la massa della nube e quella degli atomi che la compongono) e sostituendo a R l’espressione

(6)

in cui compare la densità r della nube (nei conti abbiamo impiegato anche l’espressione del volume, ecco spiegata la provenienza dei termini numerici e del π), con qualche passaggio algebrico otteniamo:

(7)

Al valore della massa che costituisce lo spartiacque tra l’espansione e il collasso della nube si attribuisce il nome di massa di Jeans (M_J) e questo spiega perché, quando si voglia valutare il destino di una nube, solitamente si chiama in causa il criterio di Jeans. Tale criterio, insomma, ci ricorda che il collasso di una nube può iniziare se diminuisce il contributo dell’energia cinetica (cioè il gas si raffredda) oppure se aumenta la sua densità.

L’ultima annotazione la riserviamo proprio a quest’ultima circostanza, esaminando un caso davvero curioso. Quando una nube interstellare viene investita dall’onda d’urto di una supernova, il gas che la compone è ovviamente soggetto a una compressione. Poiché questo comporta un aumento di densità, si possono verificare le condizioni perché inizi il collasso gravitazionale del materiale della nube. Insomma, la morte di una stella può diventare fattore determinante per la nascita di altre stelle.

---

Home Spigolature

Livello Base