Si consideri un laser
che emette radiazione elettromagnetica di una ben precisa lunghezza d’onda 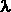 o.
Questo significa, assimilando l’onda elettromagnetica ad una sinusoide,
che la distanza tra due creste d’onda – due massimi della sinusoide – è
pari a o.
Questo significa, assimilando l’onda elettromagnetica ad una sinusoide,
che la distanza tra due creste d’onda – due massimi della sinusoide – è
pari a 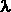 o. o.
Supponiamo che il laser sia in moto
con velocità v verso un osservatore, e che si
trovi ad una distanza L1 al momento dell’emissione
di una determinata cresta d’onda. Dal momento che la luce viaggia con velocità
c,
la cresta d’onda successiva viene emessa dopo un tempo 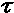 o= o=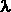 o
/ c (il tempo necessario alla seconda cresta per raggiungere la
posizione occupata dalla cresta precedente), quando il laser si trova ad
una distanza L2=L1-v o
/ c (il tempo necessario alla seconda cresta per raggiungere la
posizione occupata dalla cresta precedente), quando il laser si trova ad
una distanza L2=L1-v 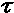 o
. o
.
Pertanto la prima cresta giungerà
all’osservatore dopo un tempo t1=L1/c,
e la seconda dopo un tempo t2=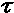 o+L2/c. o+L2/c.
Dunque per l’osservatore le due creste
d’onda si succedono dopo un intervallo temporale
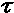 = t2 - t1 =
= t2 - t1 = 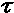 o
+ (L2 - L1) / c = o
+ (L2 - L1) / c = 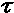 o
(1 - v/c) = ( o
(1 - v/c) = ( 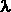 o/
c)(1 - v/c) o/
c)(1 - v/c)
Tenuto conto che anche per l’osservatore
vale la relazione generale 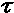 = =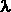 /c,
si ottiene la seguente espressione per la lunghezza d’onda della radiazione
percepita dall’osservatore: /c,
si ottiene la seguente espressione per la lunghezza d’onda della radiazione
percepita dall’osservatore: 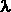 /
/ 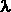 o = 1 - v/c
. Se esprimiamo la lunghezza d’onda osservata in termini della sua differenza o = 1 - v/c
. Se esprimiamo la lunghezza d’onda osservata in termini della sua differenza 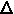 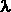 rispetto alla lunghezza d’onda di laboratorio (ovvero la lunghezza d’onda
nel caso di una sorgente immobile), possiamo scrivere
rispetto alla lunghezza d’onda di laboratorio (ovvero la lunghezza d’onda
nel caso di una sorgente immobile), possiamo scrivere
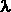 = =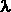 o
+ o
+ 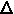 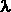 ed otteniamo la formula classica che descrive l’effetto Doppler:
ed otteniamo la formula classica che descrive l’effetto Doppler:
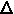 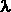 /
/ 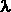 o = -
v / c o = -
v / c
Si noti che, a causa della presenza
del segno meno, la lunghezza d’onda della radiazione di una sorgente in
avvicinamento appare più corta di una quantità tanto maggiore
quanto maggiore è la velocità della sorgente. Nel caso di
allontanamento, al contrario, la lunghezza d’onda apparirà maggiore.
Dal momento che la teoria della relatività
ci dice che nessun oggetto può viaggiare a velocità superiore
a quella della luce, v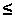 c,
sembrerebbe che nessuna sorgente possa emettere una radiazione la cui lunghezza
d’onda mostri uno spostamento superiore alla lunghezza di laboratorio, c,
sembrerebbe che nessuna sorgente possa emettere una radiazione la cui lunghezza
d’onda mostri uno spostamento superiore alla lunghezza di laboratorio, 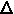 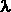 /
/ 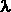 o = 1. o = 1.
In realtà sono state osservate
diverse galassie lontane e quasar che mostrano una variazione percentuale
molto maggiore. Questa apparente contraddizione è dovuta al fatto
che, nel derivare la formula dell’effetto Doppler, abbiamo assunto che
il tempo misurato da un orologio solidale con la sorgente scorra con lo
stesso tasso del tempo misurato dall’orologio in possesso dell’osservatore.
La teoria della relatività ci dice che questo non è vero,
e che in realtà per l’osservatore le lancette dell’orologio associato
alla sorgente sembrano ruotare più lentamente.
Una volta che questo effetto sia tenuto
in considerazione, otteniamo la formula relativistica per l’effetto Doppler
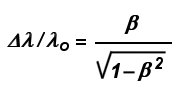
in cui, per semplicità di notazione,
abbiamo posto 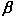 = v/c. = v/c.
Effettivamente, per velocità
relativamente basse, 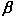 <<1,
il radicando può essere assimilato ad 1, e la formula torna ad essere
quella classica che abbiamo ricavato più sopra. Tuttavia, per sorgenti
dotate di una velocità inferiore ma simile a quella della luce, <<1,
il radicando può essere assimilato ad 1, e la formula torna ad essere
quella classica che abbiamo ricavato più sopra. Tuttavia, per sorgenti
dotate di una velocità inferiore ma simile a quella della luce, 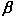 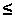 c,
il denominatore diventa estremamente piccolo, e la variazione percentuale
della lunghezza d’onda può crescere a dismisura. c,
il denominatore diventa estremamente piccolo, e la variazione percentuale
della lunghezza d’onda può crescere a dismisura.
|