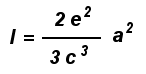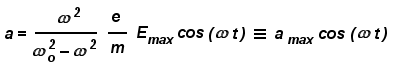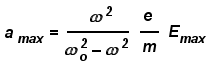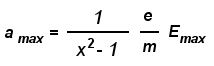|
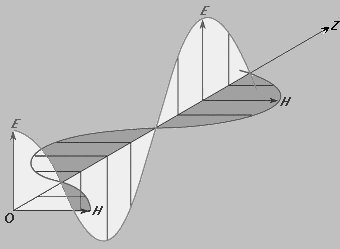
Se poniamo un elettrone in
un punto dello spazio attraversato da un’onda elettromagnetica, questo
elettrone comincerà ad oscillare "su e giù" rispetto alla posizione
iniziale in risposta al campo elettrico oscillante dell’onda, proprio come
farebbe un sughero galleggiante sull’acqua quando è investito da un’onda.
Al contrario del sughero, tuttavia, l’elettrone, possedendo una carica
elettrica e, emette radiazione la cui intensità I è data da
|
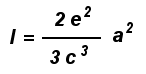
|
(1)
|
dove c è la velocità della luce, e
la carica dell’elettrone ed a la sua accelerazione.
Dunque un elettrone inizialmente fermo non emette radiazione. Una volta
investito da un’onda elettromagnetica, però, l’elettrone sperimenta
un’accelerazione alternata della stessa frequenza dell’onda incidente ed
emette a sua volta radiazione di frequenza pari a quella del fascio
incidente. In altri termini, la radiazione è "diffusa" in
tutte le direzioni.
Questa diffusione viene detta Thompson scattering, e la sua
efficacia non dipende dalla frequenza della radiazione incidente.
Se però l’elettrone non è libero, ma posto
in un atomo (come accade nell’atmosfera), le cose vanno diversamente.
In questo caso l’elettrone (negativo) è legato al nucleo atomico (positivo)
tramite una forza elettrica e, per quel che concerne le argomentazioni che
seguono, il suo moto può essere assimilato a quello di una molla: l’elettrone
oscilla rispetto al nucleo, così come l’estremità di una molla oscilla
rispetto alla sua posizione di equilibrio.
E' bene, allora, accantonare per il momento, il nostro elettrone e
approfondire meglio il comportamento di una molla. Questo ci permetterà di
chiarire, successivamente, il problema dell’interazione di un elettrone
atomico con un fascio di radiazione incidente.
Consideriamo una pallina di massa m posta
all’estremità di una molla e tendiamo la molla stessa spostando la pallina
fino ad una distanza x dalla posizione di equilibrio.
La forza esercitata dalla molla sulla pallina si può scrivere come
Fm = - k x
La costante k è una
caratteristica della molla (dà una misura della sua elasticità) ed il segno
negativo sta ad indicare che la forza è sempre indirizzata in senso opposto
allo spostamento. Infatti, quando si tende la molla c’è uno spostamento
positivo della pallina su cui la molla esercita una forza di richiamo in
senso opposto; se invece comprimiamo la molla lo spostamento è negativo e la
molla spinge la pallina di nuovo in senso opposto.
Dalla seconda legge di Newton sappiamo che ogni forza, e dunque anche quella
esercitata dalla molla, può essere espressa come il prodotto della massa
m per l’accelerazione a impressa alla massa dalla forza stessa:
F = m a
Dall’uguaglianza di questa espressione con
quella data più sopra (F = Fm), otteniamo per
l’accelerazione la formula
a = - ( k
/ m ) x
Se ora lasciamo andare la molla, la
pallina posta alla sua estremità oscillerà avanti e indietro rispetto alla
sua posizione di equilibrio in un intervallo –D < x < D, dove
D è l’estensione massima dell’estremità della molla dalla posizione di
equilibrio (l’estensione a cui abbiamo sottoposto la molla inizialmente).
Si può dimostrare facilmente che il moto della pallina è di tipo sinusoidale
e può essere espresso, ad esempio, come x (t) = D cos (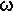 ot), dove t è il
tempo e ot), dove t è il
tempo e 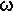 o = (k/m)0.5 è connesso alla frequenza di oscillazione o = (k/m)0.5 è connesso alla frequenza di oscillazione 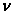 o tramite la
relazione o tramite la
relazione 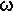 o = 2 o = 2 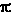 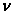 o. o.
|
Nota:
In effetti, l’accelerazione è data dalla derivata seconda rispetto al tempo
dello spostamento
a = d2x / dt2
L’equazione del moto per la pallina
all’estremità della molla è pertanto
(d2 x / dt2) - 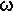 o2 x = 0 o2 x = 0
la cui soluzione generale, com’è facile
verificare, è data da
x ( t ) = D cos ( ko t + 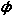 ) )
In cui D e 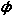 sono due costanti che
dipendono dalle condizioni iniziali. sono due costanti che
dipendono dalle condizioni iniziali.
|
In conclusione, si può dimostrare che
l’accelerazione a cui è sottoposta la pallina dopo che si è
"stuzzicata" la molla è
|
a
= 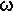 o2
D cos ( o2
D cos ( 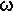 o t ) o t )
|
(2)
|
Dunque, il sistema molla+pallina non
esegue vibrazioni casuali, ma oscilla ad una ben precisa frequenza 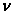 o, caratteristica del sistema
(dipende dalla elasticità della molla e dalla massa della pallina). o, caratteristica del sistema
(dipende dalla elasticità della molla e dalla massa della pallina).
Molti sistemi fisici reagiscono ad una sollecitazione esterna mettendosi ad
oscillare con una propria frequenza caratteristica. Un pendolo, una
volta scostato dalla sua posizione di equilibrio e lasciato poi a se stesso,
oscilla con una frequenza legata alla sua lunghezza (pendoli più corti hanno
frequenze maggiori). E' esperienza comune che è possibile regolare
l’ampiezza di oscillazione dell’altalena su cui si è seduti, ma non la sua
frequenza; per ottenere oscillazioni più frequenti è necessario ricorrere ad
altalene più corte. Le corde di una chitarra o un diapason
rappresentano ulteriori esempi di sistemi fisici che, una volta sollecitati,
reagiscono vibrando ad una frequenza ben precisa.
Tali sistemi vengono detti oscillatori armonici.
Possiamo ora tornare al nostro atomo e al
problema di come esso reagisce una volta investito da un’onda
elettromagnetica di data frequenza.
Nel contesto della fisica classica (ovvero in assenza di effetti quantistici)
un elettrone in un atomo può essere assimilato ad un oscillatore armonico:
esso oscilla attorno al nucleo con una frequenza caratteristica, analogamente
alla pallina posta all’estremità della molla nell’esempio precedente.
La frequenza caratteristica dipende dalla struttura dell’atomo e dalla forza
elettrostatica effettivamente esercita tra l’elettrone e il nucleo. Atomi
diversi hanno frequenze caratteristiche diverse.
Tuttavia, un elettrone atomico investito da un’onda elettromagnetica
rappresenta un problema un poco più complicato rispetto all’esempio della
molla dato più sopra. Mentre infatti quest’ultima, dopo la sollecitazione
iniziale, è libera di oscillare senza subire ulteriori interferenze esterne,
l’elettrone è continuamente sottoposto all’azione del campo elettrico
oscillante della radiazione incidente. In questo caso, oltre alla forza
di richiamo analoga ad Fm esercitata dal nucleo atomico,
sull’elettrone agisce anche la forza elettrica Fe = eE,
dove e è la carica dell’elettrone ed E è il campo elettrico
dell’onda elettromagnetica.
Quest’ultimo oscilla ad una frequenza 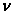 e può essere
descritto come e può essere
descritto come
E ( t ) = Emax
cos ( 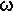 t ) t )
dove 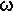 = 2 = 2 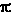 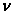 , ed Emax
è la massima intensità raggiunta dal campo elettrico. , ed Emax
è la massima intensità raggiunta dal campo elettrico.
In sostanza, F = Fm+ Fe e, tenendo
conto della formula di Newton, l’accelerazione dell’elettrone è data da
a = - 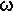 o2 x + ( Emax /
m ) cos ( o2 x + ( Emax /
m ) cos ( 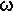 t ) t )
dove ora m rappresenta la massa
dell’elettrone e 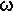 o la sua frequenza caratteristica. Questa
equazione rappresenta un’oscillazione forzata, ed ovviamente coincide
con l’equazione dell’oscillatore armonico in assenza di forze esterne (Fe
= 0). o la sua frequenza caratteristica. Questa
equazione rappresenta un’oscillazione forzata, ed ovviamente coincide
con l’equazione dell’oscillatore armonico in assenza di forze esterne (Fe
= 0).
Non è difficile mostrare che, nel caso di un’oscillazione forzata, si ottiene
|
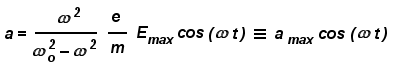
|
(3)
|
Dunque, l’elettrone
"intrappolato" nel campo elettrico oscillante della radiazione
incidente è forzato ad oscillare con la stessa frequenza di quest’ultima
anziché con la propria. Inoltre, ed è questo il punto importante,
l’accelerazione massima
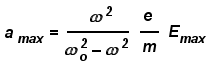
a cui è sottoposto l’elettrone dipende sia
da 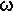 che da che da 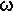 o. o.
Ponendo x = ( 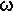 o / o / 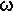 ) la formula precedente può essere riscritta come ) la formula precedente può essere riscritta come
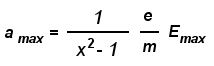
Se l’elettrone viene colpito da un’onda
elettromagnetica di frequenza simile a quella propria di oscillazione (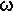 ~ ~ 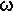 o),
x assume valori vicini
all’unità; il denominatore nella formula precedente diventa piccolo e
l’elettrone subisce un’accelerazione elevata riemettendo (diffondendo) la
radiazione in tutte le direzioni. o),
x assume valori vicini
all’unità; il denominatore nella formula precedente diventa piccolo e
l’elettrone subisce un’accelerazione elevata riemettendo (diffondendo) la
radiazione in tutte le direzioni.
Al contrario, se 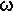 e e
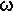 o
hanno valori molto diversi, amax è piccolo e
l’elettrone sperimenta un’accelerazione così piccola da non essere in grado
di riemettere efficacemente (si veda l’equazione 1). Come accennato in
precedenza, se comunichiamo ad un’altalena impulsi con una frequenza diversa
da quella propria, non siamo in grado di amplificarne le oscillazioni. o
hanno valori molto diversi, amax è piccolo e
l’elettrone sperimenta un’accelerazione così piccola da non essere in grado
di riemettere efficacemente (si veda l’equazione 1). Come accennato in
precedenza, se comunichiamo ad un’altalena impulsi con una frequenza diversa
da quella propria, non siamo in grado di amplificarne le oscillazioni.
In conclusione, contrariamente al Thompson
scattering che è indipendente dalla frequenza, gli atomi diffondono più
efficacemente la radiazione con frequenza vicina a quella loro propria di
oscillazione, mentre risultano “trasparenti” alle onde di frequenza diversa.
Questa diffusione selettiva è detta Rayleigh scattering e dà la
spiegazione del colore blu del cielo. Le molecole che compongono l’atmosfera
hanno frequenze proprie grandi rispetto a quelle della luce visibile (x >>1);
dal momento che la radiazione che percepiamo come blu ha una frequenza doppia
rispetto al rosso, la luce blu è diffusa molto più efficacemente. Dunque la
luce blu ci arriva da ogni direzione, e noi vediamo il cielo blu.
|