|
|
|
|
|
|
|
|
|
Il battito delle Cefeidi
Claudio
Elidoro
|
Poiché i dati indicano che una
Cefeide pulsa ritmicamente, proviamo a ragionare su questa oscillazione
periodica partendo dalla formulazione delle oscillazioni di un pendolo,
dunque dalla relazione P
= 2p
Ö
l/g Ovviamente sarà ora
necessario sostituire alla lunghezza l
del pendolo il raggio R della
stella e all'accelerazione di gravità g
l'accelerazione di gravità della stella che, indicando con M la sua massa e con G la costante di gravitazione
universale, sarà GM / R2. Otteniamo in tal modo P
= 2p
Ö
R3/GM e dunque P µ
R3/2. Poiché la luminosità L di una stella – oltre a dipendere
ovviamente dalla temperatura (legge di Stefan-Boltzmann)
– dipende anche dalla sua superficie ed è dunque proporzionale a R2, possiamo scrivere che
P µ
L3/4. Ma noi sappiamo anche
che L µ
2,5–m, in cui m è
la magnitudine e il segno negativo deriva dalla scala scelta per misurare le
magnitudini stellari. Questo comporta che P
µ
2,5–(3/4)m e dunque, introducendo due costanti k1 e k2 per non impantanarci
nei conti (vista anche la natura qualitativa del ragionamento che stiamo
seguendo), possiamo scrivere che log10 P = – k1
· m + k2. Da questa, tenendo
conto del legame tra m e Mv
e della necessaria calibrazione per mettere in linea la
scala della distanza, possiamo giungere alla tipica relazione P-L delle Cefeidi,
vale a dire Mv = – a · log10 P – b. Proviamo ora, giusto
per vedere la relazione P-L all'opera, a calcolare la distanza di ζ Geminorum (per gli arabi Mekbuda,
la zampa del leone), una stella appartenente al gruppo delle Cefeidi
classiche. Le osservazioni della sua luminosità, alla portata anche di
osservazioni amatoriali, ci indicano che in un periodo di 10,15 giorni la
magnitudine oscilla tra un massimo di 3,62 e un minimo di 4,18. Questo
comporta che la sua magnitudine media apparente mv valga 3,90. Applicando la
relazione P-L a questa Cefeide (utilizziamo i parametri suggeriti da Michael Feast e Robin Catchpole, mnras,
1997), otteniamo che: Mv
= – 2,81 log10 (10,15) – 1,43 = – 4,26. Tenendo presente che
la relazione che lega tra loro magnitudine apparente (m) e magnitudine assoluta (M) al variare della distanza (d) espressa in parsec – si veda a tal proposito la «Spigolatura»
pubblicata nel giugno 2003 – è data da Mv = mv + 5 – 5 log10 (d), possiamo ottenere l'espressione
della distanza come d
= 10 (mv – Mv + 5)/5. Facendo dunque i conti,
otteniamo che d
= 10 (3,90 + 4,26 + 5)/5 = 102,63 = 426 pc. La consultazione
online della banca dati astronomici Simbad ci
permette di recuperare la parallasse di ζ Geminorum
misurata dal satellite Hipparcos, pari a 2,79 milliarcsec (± 0,81). Secondo la misura di parallasse,
dunque, la stella dista tra 278 e 505 pc, un
intervallo entro il quale il valore da noi calcolato si adatta alla
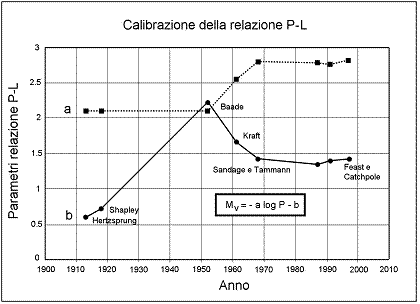
perfezione. Dedichiamo un ultimo
accenno alla problematica calibrazione della relazione P-L e lo facciamo
semplicemente presentando un grafico (Fig.
4) che mostra il variare dei due parametri della relazione (pendenza e
punto zero) da quelli impiegati nel 1912 (Hertzsprung) fino a quelli del 1997
(Feast e Catchpole).
Fig.
4. Andamento dei parametri della relazione
P-L proposti da vari astronomi nel corso degli anni. Anche se il grafico si
estende fino al 2000, non si creda che l'argomento sia definitivamente
risolto. In uno studio del 2009, per esempio, Zhang
Hong e Zhu Zi correggono
i valori di Feast e Catchpole
dopo la revisione dei dati di Hipparcos. Piccoli
aggiustamenti, comunque, e non drastici interventi come quello di Baade nel 1952. |