Chapter I

ORIGINS AND PHASES OF THE “BLACK DROP” PHENOMENON

Previous theories – Apparently, the phenomenon of deformation of the edges perceived by the eye to a large or small degree and with a fair light and distance around the place of apparent or actual contact between two bodies, began to be investigated in 1761, after the first transit of Venus across the solar disk was observed with adequate instruments[1].

The first observers called it “gutta nigra”, (dark ligament, black drop, ligament noir, Tropfen, etc.) and formulated a number of hypotheses in order to explain it. Many believed that this phenomenon originated in the sky and thus had celestial causes; others attributed its origins to observing instruments. In this paper, I will have the chance to mention either one or the other of the following causes: 1) Irradiation of sunlight; 2) Atmosphere of the Planet; 3) Turbulence of the Earth’s atmosphere; 4) Diffraction of light and its effects on the images that form in optical instruments; 5) Spherical aberrations of lenses and eyepieces 6) Imperfect adjustment of the eyepiece 7) Polyopia.

Undoubtedly, none of these causes should be put aside while studying the “drop”, because each cause can partly give rise to some of the numerous aspects that are summarised by this single word. On the other hand, even their simultaneous action does not succeed in justifying the complex but logical sequence of all the phases, since some of them have always escaped the observers’ attention. Thus, in order to reconstruct the whole phenomenon, we should use data from different sources choosing only those details in the astronomers’ descriptions that were clearly observed, while leaving out all the others.

To compensate the rarity of this phenomenon – which is getting rarer due to frequently unfavourable atmospheric conditions – and simplify astronomers’ research into its nature, Struve suggested to reproduce the phenomenon artificially by placing conveniently overlapping bright and dark disks far from the observer. The most authoritative tester of this method, G.van de Sande Backhuyzen[2] concluded, on the basis of his telescopic observations of the artificial transit that the “drop” resulted from the diffraction of light through the objective lens. His interpretation immediately found imitators and followers and today, after almost fifty years, it is still generally[3] agreed that this phenomenon is due to the cause pointed out by Backhuyzen. He also considered the idea of polyopia, but only mentioned it as playing a minor role: “Ich glaube mich deshalb berechtigt, zu constatieren, dass für mein Auge und für die von mir angewandten Fernrohre die Polyopie nur eine untergeordnete Rolle bei der Bildung des schwarzen Tropfens spielt”[4] and further on: “...glaube ich doch, dass die Diffraction die Hauptursache ist, und will deshalb auch bei den anderen Phasen des Venusvorüberganges seinen Einfluss bestimmen”.[5] Yet, even if these experiments were carried out without a telescope, i.e. by observing the disks with the naked eye and thus without the intervention of instrumental diffraction, the phenomenon would have still been observed so that those in favour of the diffraction theory would have been forced to look for another cause and precisely, as I will try to demonstrate, an extremely common eye defect, namely, astigmatism.

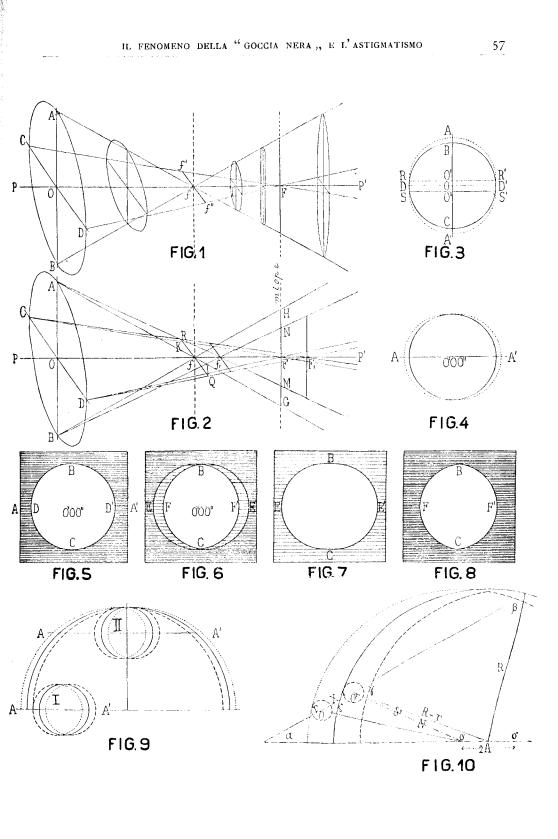
Sturm’s Theorem – The total effect of the refracting means of the astigmatic eye can be explained – as with the spherical eye – by placing a single ideal surface about 2 mm behind the front surface of the cornea (reduced eye). Usually, in the astigmatic eye, this ideal surface presents the maximum radius of curvature in a slightly inclined section with respect to the line of sight and the minimum radius in a section normal to the one above. In a rarer occurrence, the section of minimum radius lies on the plane of the line of sight. Generally, although there are also oblique directions, the maximum and minimum sections of curvature remain orthogonal.

Sturm’s[6] theory of caustic surfaces states that if the chief ray of a sheaf radiating from an infinitely far point usually intersects at point O (pag. 57 Fig.1) with a toric surface – circularly limited by a diaphragm also centred at point O, where the sections of maximum curvature AB and minimum curvature CD intersect at a right angle – the rays of this sheaf refract so as to converge in two orthogonal focal lines passing through f and F. The former lies on the plane of the section of minimum curvature CD and contains the focus of the section of maximum curvature AB whereas the latter lies on the plane of the section of maximum curvature AB and contains the focus of the section of minimum curvature CD. If the planes are perpendicular to PP’ but do not pass through f or F, the resulting images will generally be ellipses either with their major axis parallel to CD - if they are on the left of point T - or parallel to AB - if they are on the right of point T. If the plane passes through T, the resulting image will be circular since point T lies halfway between f and F, but closer to f.

Now, the fact that the pupil’s diameter is automatically reduced to its minimum in very bright light – thus getting closer to the ideal condition described by Sturm’s Theorem – can be applied to the real case of the astigmatic eye. Moreover, if the surface of maximum curvature of this eye is parallel to the vertical and the minimum is parallel to the horizontal (as in Fig.1 pag.57), the image of the infinitely far point thrown onto the retina will have the shape of a straight line segment. More precisely, if the retina - normal with PP’ - passes through F, the line segment will be vertical whereas through f, it will be horizontal.

Apparent deformation of celestial bodies – Given the shape taken by the image of a point on the retina of an astigmatic eye, it will be easy to reproduce the image of a celestial body thrown onto a sphere in the shape of a circular disk. Instead of a circle, this image will correspond to Fig.3 or Fig.4, depending on whether the retina contains the focal line F or f. The two semi-circumferences DBD’ and DCD’ - forming a whole circumference when they both have their centres in O – contribute in all their length and with no deformation whatsoever to form the profile of the deformed image when their centres are shifted to O’ and O’’, respectively. In order to close the profile of the deformed image, we need two straight lines RS and R’S’, both as long as the focal line and tangent to the circle at points D and D’. In other words, it is possible to obtain the deformed image ARSA’S’R’ directly from the circle, provided that each point of it dilates in either directions and parallel to the straight line AA’ (which we shall call maximum radial deformation line), thus turning into a straight line segment as long as the focal line.

Yet, a closer look at this phenomenon shows that deformation caused by astigmatism is also subordinate to the relationship between the luminous intensity of the image and that of the background on which it is cast. Indeed, Fig.5 shows how a bright disk on a black background would appear to a spherical eye: we distinguish a white and a dark area, both bordering on circle BDCD’. The dilation caused by astigmatism, whose line of maximum radial deformation is AA’, will take the circle BDCD’ both to BECE’ (Fig. 6) – thus becoming the new external border of the dilated bright area – and BFCF’ – thus becoming the new internal border of the dark area, dilated in turn. As a result, we have the original whiteness characterising the internal area BFCF’ and the original darkness characterising the area external to BFCF’, respectively, whereas the area between the two curves BECE’ and BFCF’ shows a mixed colour made up of an equal measure of black and white. Furthermore, if the brightness of the luminous disk overcomes the darkness of the background, the astigmatic eye will see Fig.5 deformed into Fig.7; on the other hand, if the surrounding blackness definitively prevails on the weak light of the internal area, such eye will see Fig.5 deformed into Fig.8. Only extremely sensitive eyes will also be able to distinguish the intermediate coloured area comprised between the blackness of the background and the brightness of the image.

Two well-known examples concerning the prevalence of light over darkness are available to astronomers, i.e. the solar image projecting on a dark background sky (through the obscuring device) and the dark faces of inferior Planets projecting on the solar disk. Since in both cases powerful sunlight takes over nearby darkness, the Sun’s disk appears dilated while the Planet’s disk appears contracted. In order to avoid any confusion with the phenomenon known as “irradiation”, I would like to point out that these deformations have – in the radial sense – their maximums and minimums placed symmetrically according to the observer’s astigmatism.

Apparent contacts of celestial bodies – Let AA’ in Fig.11[7] be the line of maximum deformation coinciding with the line joining the centre of the Sun to the centre of the Planet. Continuous lines S and V outline the actual limits of the two disks while terminators S’ and V’ outline their apparent limits and line segments S’’ and V’’ their latent limits. By apparent limits, I mean those perceived by the astigmatic eye (instead of actual limits, perceived only by the spherical eye) whereas by latent limits S’’ and V’’ I mean those that are not visible until the two disks are far away from each other, as in Fig.11, but that will manifest themselves during the transit, either preceding or following the contact, as I shall now describe. The four thicknesses SS’, SS’’, VV’ and VV’’ are identical with regard to celestial bodies, which are at the same distance – or virtually so - from the observer.

We know that the light intensity of the areas comprised between limits S’S’’ and V’V’’ competes with that of the solar disk. Yet, as the two bodies make contact and latent limit V’’ crosses latent limit S’’ (Fig.14), the crescent - a mixture of two parts of darkness and one of light - comprised between such limits will be significantly darker than the surrounding area (although its darkness will equal neither the background sky nor the dark face of the Planet). This crescent, which is limited by the Planet’s edge, on the left of those observing Fig.14, and by the Sun’s edge, on the right, will be completely surrounded by light.

If we follow the Planet during its motion of egress from the solar disk, as it reaches the furthermost point of the latent limit V’’ in contact with S (and consequently V with S’’), Fig.18, we immediately perceive continuity among three dark regions: 1) background sky, 2) crescent or detached limb, 3) Planet’s disk, because of the simultaneous appearance of two identical straight line segments “a”, which have given this phase – as well as the whole phenomenon – the name “dark ligament” or “black drop”. This phase is totally justified by Sturm’s Theorem. According to it, each luminous point produces a straight rather than a point-like image on the retina of the astigmatic. Consequently, the furthest point of the detached limb of the Planet covers a point on the actual edge of the Sun so that there will be a luminous line segment of 2a in length rather than a luminous point on the retina. Such line segment lies on the line of maximum deformation AA’ with its midpoint where V’’ meets S; the same can be said of the length and position of the luminous line segment whose midpoint is where V touches S’’, which will disappear when the furthest point on the actual edge of the Planet will be occulted by the right edge of the detached limb.

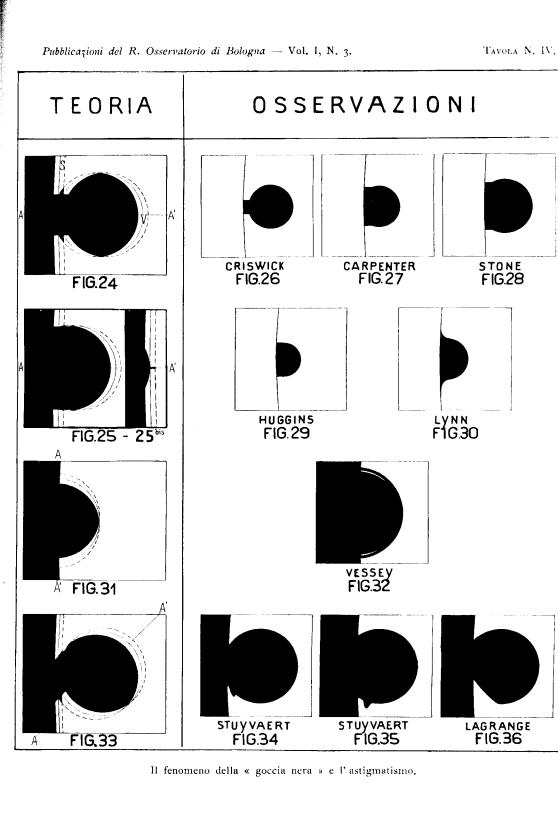
As the Planet moves forward in the same direction, an increasing number of luminous points on the actual edges of the two bodies S and V will be occulted and the corresponding images of the luminous line segments will be replaced by an equal amount of dark line segments, as shown in Fig.24, until the Planet - before reaching the actual solar limb with its centre, (Fig.25) - takes the peculiar shape of a capital “D”. By following the Planet until its complete darkening on the solar disk, it is possible to reach, through different stages of easy geometrical construction, the occultation of a single point on the actual solar limb (Fig.25 bis), where one of the straight line segments in Fig.18 reappears.

Although in the above-mentioned six figures the line of maximum deformation passes through the centres of both disks, this does not always occur. Indeed, if the line AA’ is inclined with respect to the line joining the centres, in an advanced phase of this phenomenon the ligament will assume an oblique direction (Fig.33) that will be confirmed further on by the observers’ descriptions.

In a peculiar case, the line of maximum deformation could be orthogonal to the line joining the centres (Fig.31). Hence, it would be possible to better witness the flattened shape of the visible part of the Planet (Fig.31) when half of the Planet’s circumference is off the Sun’s limb rather than when it is fully on the disk of the Sun.

Halos – Until now we have imagined that the background sky and the dark face of the Planet show the same degree of darkness through the obscuring device, which protects the eye from excessive sunlight. However, in some cases, i.e. when using no protection or just a thin obscuring device when the Sun is very low on the horizon or veiled by fog, the background sky looks considerably less dark than the dark face of the Planet. In these cases, being the Planet’s disk partly on and partly off the solar disk (despite all research, there is no reliable observation of the Planet completely off the Sun), the astigmatic eye will perceive a crescent around the non-overlapping part. This crescent consists of mixed light and looks clearer than the Planet and darker than the background, as in Fig.37, so that the observer will have the impression that the Planet’s disk is surrounded by an atmosphere.

As to the crescent opposite the one mentioned above, VV’’ (Fig.37), we have always assumed that the sunlight is so bright that it cancels the effect of the Planet’s dark colour. Yet, in some cases, extremely sensitive astigmatic eyes are able to distinguish even a slight difference between the sunlight and the light of the crescent V’V’’, thus regarding the Planet – especially when it is fully on the solar disk – as surrounded by a halo. As we will see further on, some observers considered this halo weaker than the Sun while others considered it so bright that it looked shinier than the very Sun.

Of course, when the line of maximum deformation AA’ is inclined with respect to the line joining the centres, the appearance of the halo surrounding the non-overlapping part of the Planet corresponds to Fig.38.

Chapter II

COMPARISON WITH THE OBSERVATIONS

Detached limb – This phase, unlike the others, was clearly recognized by a small number of observers. Pingré was the first to mention it. Having witnessed both transits of Venus in 1761 and 1769, he was very surprised to see that the phenomenon observed in the first transit had not occurred again in the second. In his own words[8]: “At the exit of Venus in 1761, the limbs, being not yet in contact, and even sensibly distant asunder, I saw as it were a dark spot detach itself from Venus, and gain the limb of the Sun;...at which instant I estimated the internal contact. Many have this year seen the same phaenomenon at the total entry of Venus. I was in expectation of it; neither I nor my associates perceived any such thing”.

Although the description of the missing “dark spot” may puzzle the reader, it seems that he clearly saw a detached limb and that, immediately after, during the sudden appearance of the drop, he regarded the “spot” as reaching the solar limb due to proper motion.

Chronologically, the second mention – which is much more explicit and also confirmed by a drawing reproduced in Tab. III (Fig. 15) – was by Wilson, who observed Venus transit of 1874 in Mornington (Australia). The detached limb is represented by a straight line segment that he describes as follows[9]: “there first appeared a small dark object flickering backwards and forwards between Venus and the edge of the Sun”.

During the following transit of 1882, Belgian astronomers Stuyvaert and Lagrange observed the phase of the detached limb in Texas and Chile, respectively [10]. Stuyvaert’s drawing[11] - reproduced in Fig.16 - lacks a description but clearly shows the Planet’s limb completely surrounded by sunlight. The same can be said of Lagrange’s drawing[12] (Fig.17), which comes with the following description[13]: “Un filet lumineux vient couper la goutte noire. Le disque de Venus semble se separer du bord du Soleil, mais entre ce disque et le bord il y a un filet noir à peu prés concentrique avec le Soleil”.

These two latter drawings – remarkable for their rarity – undoubtedly confirm the appearance of the detached limb and hence, in theory, they should show the curvature of the Planet on the concave edge of the crescent and the curvature of the Sun on its convex edge. However, both edges of the crescent appear equally curved i.e. in the first drawing both curvatures correspond to those of the Planet whereas in the second they both correspond to those of the Sun.

Finally, the last mention of such phase - that none of the previous theories could justify – comes from J.Tebbutt, a tireless observer of transits, who fails to illustrate his words with a drawing but describes the appearance of the first internal contact as follows[14]: “...Just at the time, when I expected geometrical internal contact to take place, the Planet became somewhat pear-shaped, its limb being connected with that of the Sun by a triangular black ligament, whose base was on the Planet, and its apex on the solar limb... The ligament suddenly broke at the same time and for fully 14 seconds the vibrations were so great that the triangular ligament was repeatedly seen separated both from the disc of the Planet and the limb of the Sun”. Rather, I tend to believe that it was precisely the extraordinary and almost unbelievable phenomenon of the detached limb that gave the observer the impression of such a turbulent atmosphere. Otherwise, amidst such meteorological turbulence, it should have been impossible for him to observe the phase of the ligament only a few seconds earlier and so accurately and even notice its triangular shape and the position of its base and apex.

Furthermore, there is a significant number of observers – probably half of those whose descriptions I read (see Table at pag.43) – who point out at least two phases of this phenomenon: 1) geometrical contact, 2) appearance (or disappearance) of the luminous ligament (in other words, the definitive separation of the two disks) and assign them different times, sometimes using intervals longer than a minute. Nevertheless, they do not mention a drop or a ligament but only shades that they try to explain in different ways. Personally, I would classify these shades as part of the phase of the detached limb, whose real nature was perceived only by the above-mentioned very lucky few. Here are just a few instances of those descriptions, yet many more could be added.

In 1882 in Potsdam, while observing the ingress of Venus on the solar disk with a refractor with an aperture of 30 cm and a magnification of 120x[15], H.C. Vogel spotted a luminous ligament (ein ganz feiner Lichtfaden) between the Sun and the Planet and wrote: “Von Trübung zwischen Venus und Sonnenrand war zu der Zeit keine Spur sichtbar; sie bildete sich erst kurze Zeit darauf, war breit und dunkel am Sonnenrande, weniger breit und weniger intensiv an der Peripherie der Venus. Diese Trübung verschmälerte sich in dem Maasse als die Venus weiter eintrat, und verschwand ziemlich rasch. Eine Tropfenbildung fand nicht statt”. In other words, this is a definition of the detached limb, which gets thinner and thinner as the area formed by the overlapping latent limbs fades away.

Similarly, in the same year Jas. Williamson, Director of the Kingston Observatory, observed the ingress of Venus on the solar disk with a 6¼ inch Alvan Clark equatorial[16]: “For a little while after”, (i.e. after what he regarded as the geometrical contact), “the limbs seemed slightly to separate, a dark shade occupied the narrow interval between them, extending a little way on each side of the former points of apparent contact... there was nothing of the so called black drop, but only the dark shade already referred to”. About egress, he said: “The dark haze seen at ingress in the morning began at this time to be again observed at egress, but the interval during which it continued, and discontinuity was noted, was much shorter than in the forenoon”.

In addition, also Dunér and Lindsted clearly deny seeing either a drop or disks’ deformations while observing Mercury transit on May 6, 1878[17] in Lund: “Eine Verzerrung des Bildes oder eine Tropfenbildung war diesmal ebenso, wenig zu sehen wie beim Durchgange von 1868”. Yet, they both give two times for the moment of internal contact:

Clearly, if the geometrical contact occurred at 6m 39s and 6m 41s, respectively, it was already over thirteen or eleven seconds later. Yet, having not seen any light between the two disks, the observers were late in declaring that the separation actually took place. I could quote many more cases with longer intervals, during which the observers saw unclear shades that prolonged the duration of the contact up to 3 minutes[18] between the two edges.

“Drop” and “Chinaman’s cap” – Any apparently foreign shape or shade showing between the two disks and affecting their geometrical contact is generically called “ligament” by observers. However, this expression should define the straight line segments in Fig.18, because they are the only ones that effectively join the two disks and look like real links suddenly stretched between the closest areas of the two celestial bodies when a luminous point of one or the other edge appears occulted to the astigmatic eye. The first observers rightly called this sudden phase “fulmen” – a very appropriate term when considering that the remainder of this phenomenon takes place very slowly and smoothly.

Among the great range of illustrations of the “drop”, some only consist of a straight line segment while others of a small extension whose end closest to the Planet appears bigger. By merging with the advanced limb of the Planet, this end gives the whole image a pear shape, which has been frequently mentioned during the different transits of Venus and Mercury.

Generally, according to observers, the direction of the straight line segment seems to be lying on the line joining the centres of the two bodies. Even though this can sometimes occur, it is not strictly necessary because it depends on the direction of the line of maximum deformation of the observing eye, which could be lying in turn. Yet, only in Weinek’s drawing[19] (see Fig.19) the ligament is considerably inclined with respect to the line joining the centres, as displayed in theoretical Figure 33, in Table IV.

The phase of the detached limb being crossed from side to side by a straight line segment (Fig.18) was observed and drawn almost exclusively by English astronomers, who named this phenomenon “Chinaman’s cap”. I reproduce, in a slightly enlarged version, one of the drawings by Morris[20] (Fig.20), who observed Venus transit of 1874 in Glenrowan (Australia) - with an 8 ½ inch Browning reflector– since it is the only one throughout literature which meets the requirements of the astigmatic theory as far as this phase is concerned. Unfortunately, Morris did not comment his excellent drawing, which is very effective nonetheless.

The drawings by Ellery, Moerlin and Russell - who were also observing the same transit in 1874[21] - are more similar to the “Chinaman’s cap” but not as close to the actual aspect of the phase. In partial agreement with the mentioned theory, see Fig.21, 22 and 23. Fig. 21 and 22 show the lack of the line segment nearest the solar edge, while Fig.23 shows the lack of the line segment nearest the Planet, although it succeeds in clearly depicting the detached limb.

Undoubtedly, the phase shown in Fig.18 is also hinted at by the astronomer Leygue, who noticed some dark fringes between the two disks[22] during Venus transit of 1882: “Ces franges etaient traversées par un ligament noir tante que le contact n’avait pas lieu et elles devenaient continues à ce moment”.

Weakening and strengthening of the Planet’s limb – These two phases, which can be considered opposite, are reproduced in Fig.25 and 31 (Tab. IV) and can be obtained with a simple construction, by taking into account the observer’s astigmatism, whose line of maximum deformation is presumably along the line joining the two celestial bodies in Fig.25 and normal with it in Fig.31. There are numerous examples of the first shape that someone called capital “D”. Higgins, who noticed it during Mercury transit of 1868, drew Fig.29 and gave the following description:[23] “The spot (i.e. the disk of the Planet) appeared distorted, spreading out to fill up partly the bright cusps of the Sun’s surface between the planet’s disc and the sun’s limb. This appearance increased as the planet went off the sun, until when the disc of the planet had passed by about one third of its diameter, it presented the form represented in the diagram in which the margin of the disc, from points at the end of a diameter parallel to the sun’s limb, instead of continuing its proper curve appeared to go in straight lines up to the limb, thus entirely obliterating the cusps of light, which would otherwise have been seen between the planet and the limb”. Such description clearly points out the progressive invasion of the bright solar cusps by the “drop”, which becomes increasingly big at egress of the Planet.

In addition, as regards the mentioned Mercury transit (1868), I reproduce another four drawings of the “D” shape by W.T.Lynn[24], G.S. Criswick[25], J.Carpenter[26] and E.J.Stone[27] in Fig. 30, 26, 27 and 28, respectively. The latter three, being more consistent with this theory, show the deformed parts in their places, as in the geometrical construction.

Other observers mention this phase without going into details, e.g. Russell[28] (Mercury 1881): “Mercury assumed a “D” shape”. It is worth pointing out that the observations of the “D” shape that I have quoted so far refer to Mercury although Liversidge[29] noticed the same appearance also during Venus transit of 1874: “...Venus appeared to be nearly one third off the Sun’s limb; there was just the slightest trace of distortion or tending to the D -form, retained until the Planet was half off; hardly perceptible”.

The observation of the opposite phase, shown in Fig.31, is rarer. During Mercury transit of 1878, it was observed, at ingress, by Geelmuyden[30] at Cristiania Observatory with a 7 inch refractor. He described it as follows: “Einschnitt als Spitze gesehen, nach einer Skizze einen Winkel von etwa 120° einschliessend”. During Mercury transit of 1868, Oppolzer[31] saw it at egress with a 4 inch instrument and claimed: “Den Ausschnitt den die Scheibe des Mercurs eine Minute vor der aüsseren Berührung in der Sonnenscheibe bildete, schien nicht entsprechend einer runden Scheibe, sondern sehr merkbar conisch, und blieb so, kleiner werdend, bis zum Moment des Verschwindens”.

            Fig. 32 illustrates the observation carried out by Vessey[32] in Woodford (Venus 1874); apart from the flattening, this drawing also shows what he calls “halo” - a subject that I shall discuss in next chapter.

            Morso di Faravella, who took part to the Italian expedition to India led by Tacchini[33], found the phenomenon outlined in Fig. 25 bis: “At  that  moment (first external contact) I did not see a circular segment on the Sun's edge but a shrp tip that soon turned into a circular arc”. And about the advanced limb of the Planet, which was about to leave the solar disk: “...the phase gradually decreased and, by then very tiny, seemed to recover
a point-like shape as in the first contact, etc.”.

            Halo of the overlapping Planet – Although the Planet’s disk, which is completely on the Sun, appears deformed because of astigmatism, it does not stop being a symmetrical image (Fig.11); the overlapping of the dark limbs of the Planet and of the bright background of the Sun results in a sort of halo of maximum thickness along the line of maximum deformation and equal to zero in an orthogonal direction to it. Such halo cannot be as bright as the Sun and is considerably less dark than the Planet, to the extent that many mistook it for its atmosphere, lit by sunlight from behind. Some regarded it as brighter than the Sun, some did not see it at all whereas others saw it either as less bright than the Sun or of different colours such as orange, violet, etc.

Undoubtedly, the halo might have looked brighter than the Sun and Huggins[34], who had the chance to see it with an 8 inch telescope (120-220x magnification) during Mercury transit of 1868, authoritatively confirms it: “Whilst carefully examining the immediate neighbourhood of the spot (the Planet’s disk) for the possible detection of a satellite, I perceived that the Planet was surrounded with an aureola of light, a little brighter than the solar disc”. And further on: “The aureola was not sensibly coloured, and was only to be distinguished from the solar surface by a very small increase of brilliancy”.

            I would also like to quote the last period of Huggins’ commentary to his observation of the halo, where he recalls similar phenomena occurring during different transits before 1868: “Similar phaenomena have been observed at some former transit. A sort of ring of faint light was seen by Plantade at the transit of 1736; also by Proserpin; also by Flaguergues in 1786, and in 1789 and 1799. He calls it “an anneau lumineux”. Mechain Messier, Fritsch, and Syffler observed a similar phaenomenon. It is also described by Schroeter and Harding during the transit of 1799. In 1832 Dr. Moll saw it as “a nebulous ring of a darker tinge approaching to a violet colour”. Some of these observers appear to have considered the aureola to be slightly brighter and others as in a small degree darker than the sun”.

            The brighter halo was also observed by Browning[35]: “slightly brighter than the solar disc”. Also Downing, during the transit of 1878, claimed: “An appearance of a ring slightly brighter than the Sun was visible round the Planet”.[36] Unlike the above-mentioned astronomers, Krone[37] observed it not only round Mercury but also round Venus: “Jetzt schwebte die kleine Venusscheibe frei in der von jetzt an laengere Zeit hell leuchtenden Sonnenscheibe, rings umgeben von einem heller als die Sonnenflache leuchtenden Lichtkreise”.

            Karlinsky[38] and Pohl[39] perceived the halo as less bright than the Sun, Borrelly[40] as “grisátre” and Gilbert[41] as “violet”.

            Clearly, if the phenomenon depends on astigmatism, the halo should appear clearer than the Planet and less bright than the solar surface; only 9 astronomers out of 63 who mention it perceived it as brighter; 11 perceived it as considerably less bright, while the others did not comment on its luminous intensity.

            Only Vessey illustrated in Fig. 32 the diverse halo’s thicknesses as symmetrically decreasing from maximum to minimum. Walter Pye[42] found that the halo was not concentric with the disk of the Planet and mentioned “the ring being narrower (to Mercury’s edge) on the side next the Sun’s limb”.

            In the Table at pag.43, it is worth noting the greater frequency of observations of the halo around Mercury rather than Venus, whereas the opposite is true of the halo, which seems to surround the Planet off the Sun – a subject that I shall deal with in the next paragraph.

            However, if the sunlight completely overcomes the darkness of the overlapping Planet, it will not be possible to distinguish the halo from the luminous background and the Planet will appear symmetrically deformed as in Fig. 11. The disk will therefore no longer appear round but oval. Fig. 12 and 13 by Mayer[43] and Bayley[44] clearly show this elongated shape.

            Nobody better than B. Ferner[45] briefly but accurately described the sight that he witnessed in 1769 i.e. the extreme transformation of the dark image of Venus about to come off the ligament that restrained it in order to appear free and fully overlapping the Sun: “The diameter of Venus, which was perpendicular to the Sun’s limb appeared the greatest while Venus was passing over the Sun’s limb; but after Venus had passed the sun’s limb, the same diameter appeared the smallest; so that Venus presented himself in both these cases under an oval form, but in contrary directions”. Here, the same cause gives rise to the consecutive “drop” and flattening phases as shown in Fig. 24 and 11.

            During last Mercury transit of 1914, the astronomers of Greenwich Observatory measured the diameters of the Planet overlapping the Sun from different position angles without finding remarkable differences (they do not say how they kept their line of sight with respect to the filar micrometer – an essential element in this type of measurements), but Jonckheere[46] said about his colleagues: “At 22h 50m Mr.Bryant observed that the horizontal diameter of the Planet looked the smaller. At 0h 5m Mr.Furner was of the opinion that the identical diameter appeared the larger and I had personally the same impression. This may be an optical illusion”.

            I shall discuss the micrometric measures of the diameters of Mercury recorded by Belgian astronomers in relation to the position of the line of sight at pag.47.

Halo of the non-overlapping Planet – Despite all the attempts, nobody has ever succeeded in clearly seeing the Planet in its inferior conjunction, unless a small limb next to the Sun revealed its presence. By following this dark line segment, some astronomers observed the supplementary limb projecting onto the sky, surrounded by a faint light.

            The observer's astigmatism can explain this light whenever the disk of the Planet appears darker than the background sky – a frequent occurrence when using low intensity obscuring devices.

            Thus, a region takes shape – as for Fig. 37 – next to the disk and the background sky but less dark than the disk and less bright than the sky. The astigmatic will then see the Planet surrounded by a halo that he will regard as clearer than the Planet.

            The region of the overlapping limbs is not a circular ring but presents – as in Fig. 37 – a maximum thickness along the line of maximum deformation and virtually a zero thickness in the orthogonal direction to it. The crescent shape that reveals the real nature of the phenomenon is largely confirmed by a significant amount of information in the astronomical annals, where the appearance is generally ascribed to the atmosphere of the Planet. Fig. 40 shows Lagrange’s drawing[47], which refers to the egress of Venus from the solar disk during the 1882 transit and is described as follows: “Le bord exterieur de Venus est eclairè; l’image est admirable et les cornes parfaitement nettes”

            However, the presence of the crescent’s maximum thickness on the line joining the centres is sheer chance whereas, generally, the line of maximum deformation forms an angle with such line, thus generating asymmetrical halos, as shown in Fig. 39 also by Lagrange and in Fig. 41, 42 and 43 taken from the descriptions by Belfield[48] and Barnard[49]. About Fig. 39, Lagrange says: “On voit le disque de Venus sur le fond du ciel, a gauche et en bas une aureole lumineuse blanche due sans doute à l’eclairement de l’atmosphere de Venus”. The line of maximum deformation and the line joining the centres incessantly vary their reciprocal position so that if they coincide at the first contact, they generally do not at the second.

            Even Langley[50], during Venus transit of 1882, was struck by the mentioned asymmetry: “The centre of this bright marginal segment was estimated, from a rough sketch made at the telescope, as being about 30° on one side of a line joining the centres of the Sun and Planet, and its asymmetrical position with reference to the horns was conspicuous”. Wright[51], in his description of Venus transit of 1874, says: “...this halo (after the third contact) gradually became brighter and was not so uniform as at ingress, but most distinguishable on the NE quadrant of the Planet”. During the same transit of 1874, Onslow[52] illustrates – with two beautiful drawings better than with his description – the asymmetry that characterises the halo off the Sun. I believe it is also worth mentioning Puiseux’s[53] words, from which I infer that the aspect described by him can be represented in Fig. 44: “Le fond du ciel est bleu, les images sont brillantes et calmes. Un quart environ du disque de Vénus est déjà sur le Soleil. Le cornes se terminent avec une netteté parlaite, mais de leur extrémité se détache une auréole pále qui entoure Vénus sur une étendue de 5° á 6° vers l’extérieur, à partir des pointes d’intersection de sa circonférence avec celle du Soleil. Je m’assure à plusieures reprises que l’arc lumineux n’est pas complet. Je substitue au grossissement de 110 employé jusqu’ici, un oculaire grossissant 160 fois. L’aspect du phénomène n’est pas modifié, non plus que par l’emploi d’un partie plus sombre du verre gradué”.

            The halo had been seen in a similar shape since 1761 around Venus by B.Wilson[54] (Fig. 45). A significant number of further observations could be quoted, yet no one except Russell and Schiaparelli mentioned the moderate darkness of the sky in comparison to the Planet – an essential condition for the appearance of this halo. Ten minutes after the first contact, Russell[55] saw “the whole of the Planet...that portion of it without the Sun, appearing on the bright sky near the Sun’s limb”; and after another five minutes he saw the halo – of which he also provides a figure. It is possible to deduce that the sky was less dark than the Planet during Schiaparelli’s observations[56] (Venus 1882), from the fact that he did not protect his eye with obscuring devices: “From  then  on"  (i.e.  after  the  first  contact)  "there was a restless movement  of more or less dense vapour through the hole in the clouds. When half  of  the Planet had already entered it, a clearer moment allowed me to see  Venus  atmosphere  in the shape of a bright arc in the dark region off the Sun".

            Advocates of previous theories did not even try to explain the presence of this halo, while observers unmistakingly attributed it to the atmosphere of the Planet – a very unlikely hypothesis, considering the different thicknesses that it shows.

Stuyvaert and Lagrange’s appendix – Despite its paradoxical appearance, this shape - which was bravely published by the scrupulous Belgian astronomers exactly as they saw it - is nothing but a logical consequence of the cause that was used to explain the other phases. The more divergent the line of maximum deformation from the line joining the centres, the clearer the shape. In Fig. 33, this divergence amounts to 45°. About his drawings, Stuyvaert[57] says: “La corne septentrionale (i.e. of the Sun) se termine en deux dents en forme de scie” and Lagrange[58]: “La corne inferieure du Soleil empiète sur Venus tout en restant parfaitement geometrique”.

Vessey’s “bulge” – A 60° inclination of the line of maximum deformation with respect to the line joining the centres causes the further limb of the Planet projecting onto the Sun to appear as shown in Fig. 46. It shows, on an exaggerate scale, the essence of the asymmetrical swelling that Vessey (Venus 1864)[59] called “bulge” and illustrated in Fig. 47 and 48, describing it as follows: “Fig.47... the Planet slightly flattened on that portion of the limb nearest the Sun’s centre, and with a slight bulge near the northern termination of the limb” and “Fig.48... Venus was not quite circular, the curve of the Planet’s limb being slightly flattened on the eastern side, with a slight bulge on the western side”.

Discontinuity and intermittence of the phenomenon – The first critics of the observations of the contacts found it strange that some astronomers saw the drop’s phases while others could not find them despite looking for them and, stranger still, that the same observer would perceive this phenomenon during one transit, but not during the next[60]. There is an even more peculiar – though very rare – occurrence (see statistical Table at pag. 43): the same observer, using the same instrument, sees two internal contacts but the first is characterized by the appearance of the drop while the second is perfectly geometrical or vice versa. Fig. 9 shows the ideal configuration for the phenomenon to reach its maximum in contact I and to equal zero in contact II. This occurs when the line of maximum deformation AA’ coincides with the line joining the centres in the first case whereas it is orthogonal to it in the second case. If the two above-mentioned lines formed an identical angle in both contacts, the duration of the contact would be the same in each case, otherwise durations would be different.

The times below, concerning observations dating back to 1769, are chosen from a list of durations of internal contacts during Venus transits of 1761 and 1769, as compiled by Dubois[61]:

The following times, relative to the transit of Venus of 1874[62], show greater differences:

Quite frequently, observers saw the “drop” only in one of the two contacts: Heraud[63] saw it only in the first contact during both Venus transits of 1874 and 1882. Whyte[64], during Mercury transit of 1881, asserted that “When about two thirds of the Planet had entered on the Sun’s disc, it assumed a pear shape”, hence: “At egress the definition was exceedingly good; the contacts were formed without distortion or clinging”. In the first contact of the same transit, Moerlin[65] noticed “a cloudiness between the edge of the Sun and the Planet, before a complete separation took place” and thus “the contacts at egress I consider good, no ligament or bead having been seen, but a clear and comparatively sharp contact”. Finally, during Mercury transit of 1914 Storey[66] observed: “The first internal contact was well seen, the black drop phaenomenon being very persistent”; while about the second internal contact he warned that “the contact was noted on this occasion as quite clear, no ligament of any kind being visible”.

            Before closing this chapter, I would like to mention a case of intermittent apparition of the ligament, which first formed and later dissolved from the observer’s sight. The observer put it down to atmospheric turbulence, yet intermittence never fails when, during observations, the astigmatic observer changes the position of his head and, consequently, of the line of sight - as it generally happens to those whose body and head have been in an uncomfortable position for a long time.

            As a matter of fact, in two consecutive figures of Venus egress (1874), Russell[67] clearly shows, respectively, the presence of the “drop” and Venus disk (which is closer to the Sun than in the previous instant) separated from the Sun by a very distinct interval. Figures aside, here are his words: “During one of these (moments of bad definition) at 3h 53m 53s, 59 the limb of the Planet nearest the Sun’s limb seemed to be in a state of vibration, as if portion of its blackness were jumping over to the Sun, which lasted only a few seconds, the vibrations being estimated at 6 or 7 per second[68]; after this the limbs recovered their perfect definition[69] and were clearly and steadily separated by a line of light, which at 3h 54m 26s, 30 could not have been more than a half a second of arc in thickness”. One cannot help being surprised by the fact that the atmospheric turbulence pictured in Figure 1 could be followed after only 32 seconds by such a quiet that allowed either limbs to maintain a perfect definition.

Observations statistics– The numerical table in the following page contains a statistical survey of 504 descriptions of Mercury and Venus transits on the solar disk and includes the last four Venus transits and seven Mercury transits, starting from 1868. The novelty and variability of the phenomenon confused observers, who consequently found it difficult to describe it. Hence, descriptions are often marred by contradictions and make classification a very difficult task. For instance, many deny having seen the “drop” but give two or three contact times up to 60 secs. or more. Yet, in theory, to anastigmatic eyes endowed with normal sensitivity, these contacts should last an instant or a few seconds at most. These contradictory cases are under the column headed “drop / seen”. I have not included those who saw the “drop” in both contacts because they are under the column headed: “longer duration in one than the other”, since I have never found two identical times as to the duration of ingress and egress.

The Table does not need further explanations. Moreover, given the numerous natural and artificial causes that contribute to the major or minor visibility of the phenomenon, it would be unwise to draw conclusions that cannot actually be drawn from numerical data.

OBSERVATIONS STATISTICS

Chapter III

CALCULATING THE DURATION OF THE PHENOMENON

Quantity of deformation according to the astigmatism in dioptres – The schematic eye - which Listing called reduced – is made up of only two components and has only one refracting surface with a 5,117 mm radius of curvature[70]. Given such radius and the following indexes of air refraction and vitreous humour:

n = 1, n₁ = 1,3465, it is possible to obtain from the well-known formula: f₁ =   n₁r    

                                                                                                                                                   n₁-n

the distance of the second focus: f ₁=19,88 mm. If the retina is at such distance from the refracting surface, the eye will be emmetropic i.e. rays coming from an infinitely distant point will converge without adjustment on it, forming a point-like image. Conversely, in the astigmatic eye the refracting surface is toric. The radius of curvature r = 5,117 and the respective focal distance f₁ = 19,88 mm are relative only to the horizontal section (line of sight) of such surface while the vertical section has a stronger curvature. The following table displays increasingly short radii and focuses of the vertical section, starting from case I where the radius is identical to the one of the horizontal section, as in an ideally perfect spherical surface. The well-known formula[71]

   n₁ _  n    =   n₁-n

 x₁      x            r

yields the value of the radius of curvature “r” of the vertical section when the punctum remotum is respectively: x = -8, -4... -1 metre. In these cases, provided the curvature of the horizontal section is emmetropic, the observer’s astigmatism is equal to ⅛, ¼...1 dioptres. The distances of the second focuses, corresponding to the radii mentioned above, are in the column headed f₁.

            As shown in Fig.1, the dimension of the straight line segment f’f” = 2A is directly proportional to both the length of the arc OD – i.e. the 1 mm radius of the pupil – and to the relationship between the distances OF, Of. The last two columns of the table below include the values of A in millimetres and in arc seconds, which correspond to the defect of astigmatism considered in cases I...V.

Duration of the phenomenon – Since very few observers saw the first phase of the phenomenon, namely, the detached limb, it is generally agreed that the duration of the phenomenon corresponds, respectively, to the interval between the sudden formation of a very thin limb (Fig.18) and the so-called geometrical contact, at egress (Fig.24), and the interval between the geometrical contact and the sudden outbreak of light between the edge of the Planet and the background sky, at ingress.

            Said interval is geometrically represented in Fig.10 by line segment x linking centres O and O’ of the latent circumference of the Planet when tangent to both the Sun’s apparent and actual limb. Also in this Figure actual limbs are continuous lines, latent limbs are segmented lines and apparent limbs are dotted lines. Below is the data for determining line segment x:

R =    radius of the apparent solar disk

r  =    radius of the apparent Planet’s disk

α =   angle between the line of maximum radial deformation and the path of the Planet with respect to the motionless Sun

β =    angle on the Sun’s actual edge, comprised between radius R and the path.

This data is used to calculate auxiliary angles γ, ς, and δ as well as line segments N and x . As a result:

and since the Planet’s speed with respect to the motionless Sun is known, it is easy to obtain the duration of this phenomenon. Yet, those who might seek consistency between observations and calculations should not forget that, if on the one hand the appearance and disappearance of the drop can be observed accurately and occur in an instant – which is why the first observers called it fulmen – on the other hand, the so-called geometrical contact or tangency of the disks is much less precise for the severely astigmatic eye because in that moment the Planet in Fig. 24 has lost its circular shape. Hence, even the indication of tangency is rather arbitrary and it seems to be the outcome of supposition rather than proper observation.

Astigmatism of astronomer G. Van Biesbroeck deduced from his observations – While measuring the diameters of Mercury’s disks during its penultimate transit of 1907, the astronomers of Uccle Observatory had a brilliant intuition i.e. that the measure of these lengths were somehow influenced by the inclination of the line of sight. Every single measure was therefore accompanied by the explanation that the line of sight was parallel or perpendicular to the pair of cross-hairs tangent to the Planet’s disk. From their distance it was possible to deduce the length of the disk’s diameter[72].

            The aim of the astronomers was to discover whether Mercury’s globe was flattened. In order to assess it, they measured a great number of diameters of the Planet from different position angles. According to their programme, each diameter was measured both with a parallel and a perpendicular line of sight with respect to cross-hairs. They found that the length of the same diameter varied when the line of sight turned from perpendicular into parallel to the cross-hairs and vice versa, whereas two diameters, although orthogonal, had the same length when the line of sight was always parallel or perpendicular to both. Consequently, they reached the remarkable conclusion that the Planet’s disk was clearly circular.

            Moreover, they succeeded in demonstrating an equally relevant aspect of this problem, namely, that the apparent flattening of the Planet – of which we have many examples in fig. 12 and 13 - depends on the position of the line of sight and thus on the eye structure or, in other words, on the observer’s astigmatism.

            I then resolved to examine the elements provided by the Belgian astronomers in order to find out whether these elements were sufficient to determine their own astigmatism. I limited my research to Mr. G. Van Biesbroeck’s astigmatism because he saw the drop phenomenon both at ingress and egress, registered the Planet’s diameters and also carried out a number of measurements of a metallic sphere reproducing the Planet and placed at 1351 meters from the observer, “dans le but de rechercher les erreurs personnelles de ce genre d’observations et l’influence de l’irradation de la lumière, qui a pour effet de dimineur le diamètre apparent de Mercure”.[73]

            Below are the four observations of the double diameter of Mercury that he carried out using an Equatorial with a 38 cm (reduced to 24.5) aperture and 360x magnification and considered the best of this series. The screw value “R” corresponds to 7”, 842. The sign — indicates perpendicularity while the sign | stands for parallelism of the pair of cross-hairs with respect to the line of sight:

            To an anastigmatic eye, the double diameter of the Planet given in screw value, should have been equal to 2^r, 5198 (its apparent radius being 4”, 99 at that moment). However, the differences 2^r, 5198 – 2^r, 060 = 0^r, 4598 and 2^r, 5198 – 2^r, 050 = 2^r, 4698 show: 1) that Mr. Van Biesbroeck’s line of maximum deformation does not coincide with the line of sight or with the line orthogonal to it, otherwise one of the two differences should have been zero; 2) that the line of maximum deformation together with the line of sight - rather than with the line orthogonal to it - must inscribe a bigger angle; 3) that, considering that the screw value = 7^r, 881, Mercury’s radius – magnified 360 times and perpendicular to the line of sight – appeared to him 7” smaller than the line orthogonal to it.

            It is not possible to obtain the absolute value of the difference between the two diameters from the corresponding measures of the artificial sphere (see pag.403, Ann. Brux. Tome VI, Issue II), because of the lack of indications concerning the eyepiece (which, of course, only magnifies the diameter of the image rather than the deformation resulting from astigmatism). Nevertheless, considering the two diameters below:

it is evident that the line of maximum deformation – as with the measures of the Planet’s diameters – appears more distant from the line of sight than from the orthogonal line. An 90x magnification eyepiece leads, even in this case, to the value 7” as to the difference between the two diameters, which is identical to the one obtained previously.

            This method of measuring the diameters would have led to an accurate determination of the observer’s astigmatism if he had also tested his sight performance when observing with his line of sight in an oblique position with respect to the cross-hairs. However, the observation of only the perpendicular and parallel positions leaves the problem unsolved by merely indicating the quadrant where the line of maximum deformation lies but not the angle that it inscribes together with the line of sight. Luckily, although Mr. G. Van Biesbroeck did not have the measures concerning the oblique position, he succeeded in observing the phenomenon of the drop, both at ingress and at egress. As I will now demonstrate, the durations of this phenomenon and the measures of the diameters in perpendicular and parallel positions are both sufficient to prove his astigmatism, with the accuracy allowed by his observations.

            Assuming that the line of sight remains constantly horizontal during the observation of these two internal contacts - whose times are known[75] - by using Uccle’s values of latitude it is easy to calculate the inclination of the Planet’s path with respect to the horizontal diameter of the Sun. It is

            Now, the unknowns, i.e. 1) the inclination of the line of maximum deformation with respect to the line of sight, and 2) the number of dioptres of astigmatism of the observing eye, should have been able to justify both the 7” difference between the radii of Mercury’s image and the duration of the drop’s phases (the interval between the geometrical contact and the separation of the disks):

            By means of subsequent tests, I found out that these values can be obtained as long as the line of maximum deformation in the observing eye is inclined at 55° with respect to the line of sight[77], astigmatism is equal to ¼ of dioptres and the diameter of the pupil is 2 mm. Thus, considering the 30x magnification eyepiece that was used to observe the contacts[78] and the relative velocity of Mercury in its orbit with respect to the motionless Sun, v=0”, 103 per second[79], the calculations carried out on the formulas at page 46 provide the data in the following table, next to the observed values:

Since the hypothesis on the unknowns represents the observed values with unexpected precision, the observing eye must have been affected by a slight form of astigmatism, whose correction could have been obtained with a cylindrical lens according to the following formula:[80]

            As Mr. Van Biesbroeck learnt about the result of my calculations, he was so kind as to send me a letter dated March 25, 1922 with the formula of the lens that he always uses for his left eye during observations:

Regardless of spherical dioptres, whose correction can be easily obtained by adjusting the eyepiece, the similarity between the cylindrical quality of the formulas does not leave much to be desired.

            From the mentioned letter dated March 25, I would like to point out the following statement: “Depuis mes premières observations j’ai pris l’habitude d’employer seulement l’oeil gauche qui est meilleur, ecc.” as well as the following, which agrees with my hypothesis: “quant à l’observation du contact je suis presque súr aussi que je l’ai faite dans la position ordinaire de la téte, avee la ligne des yeux horizontale. Je n’ai pas ici mes livres d’observation en doute que j’ai noté ce point, mais ie ne crois pas que ma mémoire fasse défaut”, and finally: “Jusqu’en 1918, quoique portant des verres pendant la journée, je ne m’en suis jamais servi pendant les observations”.

            It could be objected that the observations of Mercury date back to 1907 while the ophthalmologist’s report and the mentioned formula are 11 years older, as stated in the same letter: “En 1918 mes yeux furent de nouveau examinés, cette fois avec très grand soin par un collégue de l’université”. Yet, clearly, the sections of maximum and minimum curvature generally do not vary their position whereas, as the years go by, the adjusting power of the eyes tends to weaken. Thus, there is nothing extraordinary in the fact that half dioptre of astigmatism, which in 1918 could only be corrected with the aid of lenses, was reduced to a quarter of dioptre eleven years earlier with the very strength of the ciliary muscle.

            As the observer points out, in 1907 the eye was not completely devoid of astigmatism: “en 1907 je portais des verres spheriques, l’examen n’ayant pas accusé d’astygmatisme prononcé”. The ophthalmologist did not prescribe cylindrical lenses because the difference of curvature is negligible in the everyday use of the eye whereas, clearly, it causes remarkable effects in the observation of celestial contacts.

Chapter IV

ARTIFICIAL CONTACTS

            Laboratory experiments – When experiments are carried out at close quarters and without the aid of telescopes, they allow observers to carefully examine the phase of the detached limb – an essential component of this phenomenon – by exaggerating its effects. If the two bodies in contact are placed at an identical distance from the observer – or almost identical, as for celestial bodies – the latent limbs of both bodies (Fig. 11) will be at the same distance from their respective actual limbs as well as from their apparent limbs. On the other hand, if they are placed at different distances, said limbs appear closer to or further away from their respective actual limbs, depending on the distance of the two bodies and the myopic or hypermetropic nature of the observing astigmatic eye. Consider a horizontal axis limited by the actual edge SS (Fig. 49) and not illuminated. To the astigmatic eye, it will appear on the luminous background LL with the apparent limb S’S’ whereas the latent limb S’’S’’ will go unnoticed until another body approaches it. If this second body, for instance disk D, also projects itself on the luminous background LL, it will be closer to the myopic eye than the edge SS. As a result, the interval between the apparent and the latent limbs of the disk will appear smaller than the interval between the apparent and latent limb of the edge, as clearly shown in Fig. 2.

            As a matter of fact, if the punctum remotum generates focal lines F and f, a closer point will shift them to F¹ and f¹. In this case, extreme rays Af¹ and Bf¹ will determine line segment MN instead of primitive line GH with GH>MN on the retina of the myopic person. As predicted, the apparent and latent limbs of the closest body will be less distant from the actual limb than the farthest body.

            A similar line of reasoning proves that to the emmetropic eye – all the more so for the hypermetropic eye – whose retina passes through point f in Fig. 2, the limbs of the closest body will be farther away while the limbs of the farthest edge (vertical rather than horizontal, otherwise there would be no effect) will be closer, as shown by the comparison between line IK, which corresponds to the punctum remotum and line QR, which corresponds to the closest point, being IK<QR. As a result, the detached limb will appear closer to the disk in Fig. 49 and closer to the edge in Fig. 50. These are very frequent appearances that can be commonly observed without the aid of professional laboratory devices just by carefully observing, either at home or outside and with a fair light, the continuous contacts of vertical and horizontal edge.

            However, in celestial observations the limb’s distances appear identical for both bodies, as Baily’s description[81] clearly proves: “When the ligament breaks, its motion at the moment of separation is so rapid that it is difficult, to discern, whether the broken part collapses to the Planet or to the Sun’s edge”. It is not possible to see if it disappears in one part before the other because it simultaneously disappears on both sides.

            With adequate lights, these laboratory experiments can reproduce the drop and the halo surrounding the Planet, whether overlapping or non-overlapping.

CONCLUSIONS

            By observing Tables III, IV and V - i.e. the observed series of transformations undergone by the tormented Planet’s disk when lying next to the solar limb - and by comparing them with the effects of diffraction and irradiation suggested by some researchers, it is possible to conclude that even if these two causes succeed in explaining the presence of shadows between the limbs of the two very close disks, they fail to justify: 1) the formation of the detached limb with its relative bright intervals – an occurrence, which is totally unrelated to both diffraction and irradiation, 2) Stuyvaert and Lagrange’s appendix, 3) Vessey’s bulge, 4) the halo on and off the Sun, 5) thicknesses of this halo and its asymmetry with respect to the line joining the centres, 6) appearance and non-appearance of this phenomenon to different observers using identical instruments, 7) appearance and non-appearance of this phenomenon to the same observer using the same instrument during different transits or even at ingress or egress of the same transit, and so on.

            A less valid cause than those mentioned above is the Planet’s atmosphere. Indeed, its existence has never been demonstrated and it is hardly believable given the exaggerate height that it should reach, according to observations. Such height would not appear equal with respect to all the verticals of the Planet’s surface but with its maximum and minimum a quadrant away and varying according to observers.

            The same can be said of using the Earth’s atmospheric turbulence as an explanation for the regular sequence of atypical phases, which have been seen hundreds of times in excellent meteorological conditions by a great number of observers.

            Those who attributed the observed deformations to instrumental astigmatism came closer to the real cause. We have ascribed this effect to eye’s astigmatism because very few eyes are completely devoid of it. Yet, even spherical eyes would see the same deformation effects if any of the refracting surfaces of their instrument, either the objective lens or the eyepiece, were not perfectly spherical. With the development of optical industry, this imperfection is becoming increasingly less frequent although it is not completely unlikely that the deformations observed in the first Venus transits during the XVIII century could also depend on the astigmatism of lenses.

            Such instrumental astigmatism should be considered the cause of some aspects of the photographed ligaments even if it should be noted that these aspects – as illustrated by a few authors[82] – might bear some relation with the phases that we have been researching rather than with the well-known cause of diffusion of sensitive film. Nevertheless, having not seen any plate reproducing celestial bodies in contact, I cannot express any opinion about it.

Thus, astronomers must be aware of their degree of astigmatism and correct it with well-calculated lenses every time they intend to observe contacts (limbs with cross-hairs, limbs with limbs, occultations[83], eclipses[84], etc.), so that overused expressions such as “geometrical contacts”, “moment of contact”, etc. will truly have a meaning.

If there is a low degree of astigmatism, the correction does not require the aid of lenses Indeed, while “adjusting the focus”, the astronomer should look at the image through a thin slit coinciding with the section of minimum radius of their eye. Due to the ease of adjustment characterising the eye, once removed the slit, it will also shift the focus of the section of maximum radius onto the retina.

Among astronomers, Cerasky[85] – although for different purposes - corrected his sight during Mercury transit of 1891. He placed a very narrow diaphragm in front of a self-made Galilean eyepiece: “Un petit trou est percé dans le disque” (the disk covering the eyepiece) “devant le centre de la lentille”. This trou served as stenopeic pinhole, which approximately provides the correcting effect of cylinder lenses. Indeed, according to the observer the sight displayed no deformations: “Le contact interieur a été très bien observé...il n’y avait acune goutte noire et le contact s’est fait avec une simplicitè geometrique”.

            Therefore, the widely spread belief[86] that more powerful instruments prevent the imperfection of the drop from forming during observation of the contacts, stems from the following two circumstances: 1) the luminous sheaf coming from the eyepiece – which gets smaller as magnification increases – intersects areas of the pupil and of the refracting surfaces of the eye which get smaller and smaller and thus closer to a spherical shape; 2) although magnification amplifies the image and increases the velocity of the celestial body, it does not increase the thickness of the deformation, which only depends on astigmatism. Thus, as magnification increases, the overlapping and contact between deformed limbs becomes more transient.

            The habit of avoiding the use of lenses during observations is harmful to the astigmatic astronomer, although it has shed light on what I consider the main cause of this phenomenon. Indeed, I have to give special thanks to those scrupulous and brave observers - whose work I benefited from – who, in spite of their verisimilitude, did not bother divulging apparently weird yet truthful descriptions and illustrations.

            Bologna, May 29^th 1922.

(Translated by Valentina Mengoli)