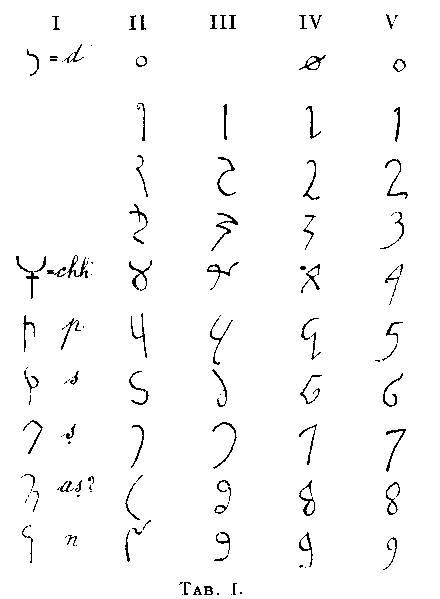
dalle "Pubblicazioni dell'Osservatorio
Astronomico della R. Università di Bologna", I, 7, 1925
CAPO I.
Le origini
Numeri arabici. - Lo studio dell'antichità indiana ha condotto matematici e filologi alla conclusione, che i cosidetti numeri arabici si usavano nell'India fin dal II secolo a. C., ed erano, quasi tutti, la lettera o la sillaba iniziale della parola, significante il relativo numero. Numeri indiani li chiamavano gli Arabi che li conobbero verso la fine dell'VIII secolo (1); noi li chiamiamo arabici, perchè essi furono introdotti dagli Arabi nella Spagna, donde nei secoli XII e XIII si diffusero nel rimanente d'Europa (2).
Non bisogna però credere che, con l'introduzione dei numeri indiani, fossero stati aboliti definitivamente presso gli Arabi gli altri sistemi usati dianzi, e per dare un esempio, nel codice arabo escurialense d'Albategno (morto nel 929) troviamo i numeri espressi ancora con lettere dell'alfabeto (3), come usavano anche altri popoli orientali; ed il Cantor (4) cita un testo d'aritmetica, compilato a Bagdad negli anni 1010-1016, ove i numeri sono ancora espressi in parole.
Le prime forme che possiamo, col Taylor, chiamare europee, si rinvengono già nei manoscritti del secolo XII, ma soltanto in quelli del secolo XIV c'imbattiamo in numeri praticamente uguali ai moderni (5).
Nella Tabella 1, che tolgo dalla già citata
opera del Taylor, si vedono accanto alle antichissime lettere-numeri dell'alfabeto
indobattriano (col. 1), i numeri indiani del sec. X (col. 2), quindi i
numeri arabici dei sec. X, XII, XIV (col. 3, 4, 5). Al nostro assunto interessa
essenzialmente l'aspetto dei numeri nell'ultimo ventennio del sec. XII,
e la metamorfosi che probabilmente subirono in quell'epoca; ad essi ritorneremo
dopo aver discorso dei simboli celesti.
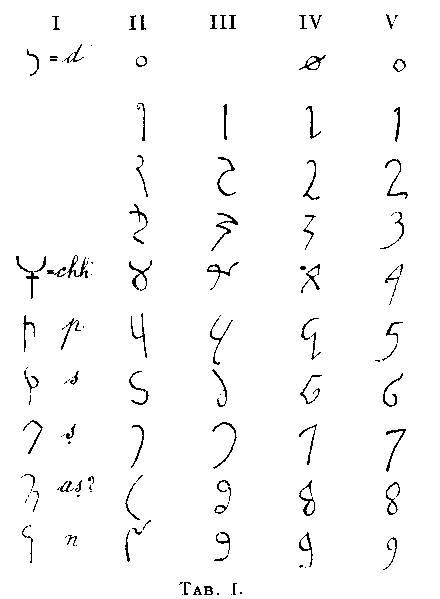
Simboli celesti - Si deve al Letronne (6) l'indagine più conclusiva sull'epoca in cui andò affermandosi l'uso dei simboli planetari: contrariamente all'opinione di G. C. Scaligero, Saumaise e Huet, egli dimostra che i simboli non risalgono affatto all'antichità classica e che, in aspetto abbastanza diverso dall'attuale, fanno capolino per la prima volta in due manoscritti del sec. X; pur variando lievemente da documento a documento, le forme che s'incontrano fino a tutto il sec. XIV sono riprodotte nella seguente Tabella (7):
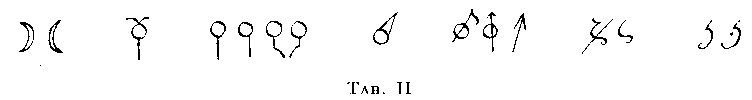
Il Letronne tace però dei simboli indicanti la congiunzione, l'opposizione, ed i nodi lunari. Questi, nelle forme rappresentate dalla Tabella III si trovano in un manoscritto greco del sec. XIV (8) di cui il Tannery (9) riproduce in facsimile la pagina che c'interessa.
Questa pagina (fol. 189 verso) contiene una trentina
di simboli, accanto ai quali si legge la corrispondente parola greca. Il
primo segno della Tabella III è contrassegnato dalla voce ![]() [diàmetros, =diametro]; con essa i Greci indicavano l'intervallo
di 180 gradi tra due segni dello zodiaco (10) ed evidentemente anche l'opposizione
di due astri erranti: la forma stessa del segno rappresenta un diametro
che porta a ciascun'estremità un altro corpo.
[diàmetros, =diametro]; con essa i Greci indicavano l'intervallo
di 180 gradi tra due segni dello zodiaco (10) ed evidentemente anche l'opposizione
di due astri erranti: la forma stessa del segno rappresenta un diametro
che porta a ciascun'estremità un altro corpo.
Nella linea successiva il manoscritto reca ripetuto
due volte il segno con cui noi indichiamo la congiunzione (Vedi
i due segni centrali della Tab. III, ma accanto ad essi si legge ![]() [emérai, =giorni] (11); non mi spiego bene l'analogia che possa
avere il giorno col simbolo della congiunzione, ma che esso
certamente rappresenti la congiunzione lo si desume non solo dalla
sua stretta parentela col simbolo dell'opposizione (è anch'esso
un diametro recante i due corpi alla medesima estremità), ma anche
dal succedere immediatamente ad esso, nell'elenco generale dei simboli
astronomici.
[emérai, =giorni] (11); non mi spiego bene l'analogia che possa
avere il giorno col simbolo della congiunzione, ma che esso
certamente rappresenti la congiunzione lo si desume non solo dalla
sua stretta parentela col simbolo dell'opposizione (è anch'esso
un diametro recante i due corpi alla medesima estremità), ma anche
dal succedere immediatamente ad esso, nell'elenco generale dei simboli
astronomici.
Finalmente si constata con meraviglia che il primo
dei due segni nodali (caput et cauda draconis, Tab. III) sia accompagnato
dall'epiteto ![]() [anabibàzon, =ascendente] ed il secondo da
[anabibàzon, =ascendente] ed il secondo da ![]() [catabibàzon, =discendente] mentre evidentemente il primo non è
altro che il nodo discendente, ed il secondo
l'ascendente.
[catabibàzon, =discendente] mentre evidentemente il primo non è
altro che il nodo discendente, ed il secondo
l'ascendente.
Veri e propri simboli non s'incontrano nei monumenti
antichissimi se non per il Sole, la Luna e Venere (Tab. IV) (12).
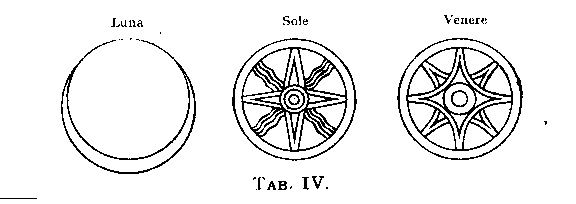
Gli altri Pianeti furono sempre rappresentati
con le immagini delle divinità di cui portavano il nome (13), accanto
alle quali si costumava però di collocare lo strumento distintivo
della loro potenza; così Giove è raffigurato con l'aquila,
Saturno con la falce, Marte con la lancia, Mercurio col caduceo e Venere
con lo specchio. Ommessa più tardi l'immagine della divinità,
il suo emblema restò a rappresentarla, e i simboli planetari divennero
col tempo i disegni nudi e schematici dei distintivi divini. Difatti in ![]() si ravvisa lo specchio, in
si ravvisa lo specchio, in ![]() il caduceo, in
il caduceo, in ![]() la falce, in
la falce, in ![]() la lancia e lo scudo, mentre non è altrettanto facile riconoscere
in
la lancia e lo scudo, mentre non è altrettanto facile riconoscere
in ![]() l'aquila di Giove; tuttavia il Frisch (14) riuscì a rivestire
convenientemente di penne quella nuda spoglia, ed a ricavarne la sagoma
del santo uccello.
l'aquila di Giove; tuttavia il Frisch (14) riuscì a rivestire
convenientemente di penne quella nuda spoglia, ed a ricavarne la sagoma
del santo uccello.
Altri videro in ![]() la folgore celeste, altri la lettera
la folgore celeste, altri la lettera ![]() iniziale di Zeus, e non sarà forse mai possibile decidere dell'origine
di un segno, che passando per tante mani subì chi sa quante modificazioni,
prima che la stampa ne sancisse la forma definitiva; a noi però
non interessano le vicende di questi simboli anteriormente al secolo XII,
ed ammettiamo che verso la fine di quel secolo essi avessero l'aspetto
che mostrano nelle Tabelle II e III.
iniziale di Zeus, e non sarà forse mai possibile decidere dell'origine
di un segno, che passando per tante mani subì chi sa quante modificazioni,
prima che la stampa ne sancisse la forma definitiva; a noi però
non interessano le vicende di questi simboli anteriormente al secolo XII,
ed ammettiamo che verso la fine di quel secolo essi avessero l'aspetto
che mostrano nelle Tabelle II e III.
Soltanto nei manoscritti posteriori al sec. XIV
e nei libri stampati le forme s'irrigidiscono nei segni sottostanti che
si usano ancora:

La
somiglianza di numeri e simboli
Confronto delle due serie. Tutti ricordano
d'aver notato la sensibile somiglianza tra il simbolo ![]() ed il numero 4, e tra il simbolo
ed il numero 4, e tra il simbolo ![]() ed il numero 5, e se, messi sull'avviso da questi due casi più evidenti,
estendiamo il confronto agli altri numeri della serie, troveremo che senza
soverchio sforzo a ciascun simbolo si può contrapporre il numero
che gli somiglia. Nel ragguaglio ci serviremo dei segni delle Tabelle II
e III, e non dei più recenti che tradiscono l'uso convenzionale
del circoletto e della croce, in varia combinazione; questi elementi entrano
nella formazione di
ed il numero 5, e se, messi sull'avviso da questi due casi più evidenti,
estendiamo il confronto agli altri numeri della serie, troveremo che senza
soverchio sforzo a ciascun simbolo si può contrapporre il numero
che gli somiglia. Nel ragguaglio ci serviremo dei segni delle Tabelle II
e III, e non dei più recenti che tradiscono l'uso convenzionale
del circoletto e della croce, in varia combinazione; questi elementi entrano
nella formazione di ![]() e più tardi con questi si creò il simbolo della Terra
e più tardi con questi si creò il simbolo della Terra ![]() e più tardi ancora quello di Urano
e più tardi ancora quello di Urano ![]() .
Considerando dunque le forme più antiche, vediamo subito che il
numero 9 è identico al simbolo di Venere, specialmente all'ultimo
dei quattro (Tab. II), il 6 ricorda il simbolo di Marte ed il 7 quello
di Mercurio; si pensi come da molti si scriva ancora il numero 7 (Tab.
V, fig. a, b), ove si riconoscono tutti gli elementi del caduceo.
.
Considerando dunque le forme più antiche, vediamo subito che il
numero 9 è identico al simbolo di Venere, specialmente all'ultimo
dei quattro (Tab. II), il 6 ricorda il simbolo di Marte ed il 7 quello
di Mercurio; si pensi come da molti si scriva ancora il numero 7 (Tab.
V, fig. a, b), ove si riconoscono tutti gli elementi del caduceo.
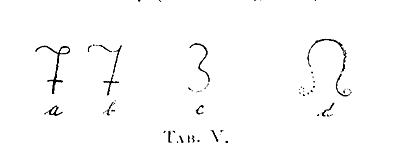
Il simbolo del Sole corrisponde allo zero
dei numeri, che in certe epoche si ridusse ad un punto, ed in altre ad
un circolo con entrovi il punto, come oggi si fa per il simbolo del Sole,
e non più per il numero. In questo caso il simbolo non è
altro che l'imitazione della forma stessa dell'astro, e lo stesso dicasi
del segno, che rappresenta la falce lunare nel primo quarto, come la si
vede nell'emisfero boreale, cioè con la gobba a destra di chi la
guarda. In questo aspetto essa rassomiglia al numero 3, e non è
infrequente il caso del simbolo lunare rappresentato da un vero e proprio
numero 3 (Tab. V, fig. c) e non solo per indicare il primo quarto, ma genericamente
la Luna stessa (15). Dopo i simboli planetari rimangono da considerare
altri tre segni usati con pari frequenza, vale a dire la congiunzione,
1'opposizione, ed il nodo (ascendente e discendente); della serie dei numeri
restano pure tre elementi, cioè: 1, 2 ed 8. Ora si vede subito che
l'8 coincide perfettamente col simbolo dell'opposizione, e che l'appendice
retta ed obliqua del simbolo ![]() è riprodotta nel-l'asta dell'unità 1. Finalmente la figura
serpeggiante del numero 2 non è altro che il simbolo
è riprodotta nel-l'asta dell'unità 1. Finalmente la figura
serpeggiante del numero 2 non è altro che il simbolo ![]() (caput draconis) quale risulta dalla scrittura abbreviata dello stesso
(Tab. V, fig. d). A corroborare il principio della somiglianza valga in
fine il vezzo di alcuni tipi numerici, che oltrepassano, ora verso l'alto,
ora verso il basso il limite della riga, in corrispondenza alle appendici
superiori od inferiori dei rispettivi simboli, come si vede dal confronto
delle due serie:
(caput draconis) quale risulta dalla scrittura abbreviata dello stesso
(Tab. V, fig. d). A corroborare il principio della somiglianza valga in
fine il vezzo di alcuni tipi numerici, che oltrepassano, ora verso l'alto,
ora verso il basso il limite della riga, in corrispondenza alle appendici
superiori od inferiori dei rispettivi simboli, come si vede dal confronto
delle due serie:
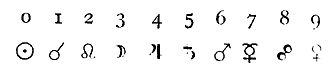
Scriviamo dunque la serie dei numeri di fronte
a quella dei simboli (Tabella VI) e cerchiamo d'interpretare il significato
astronomico dei simboli celesti così ordinati:
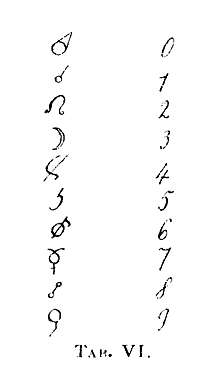
Significato dei simboli ordinati secondo la
serie dei numeri naturali - Se prendiamo il gruppo dei primi quattro
simboli ci accorgiamo che essi, nel loro insieme, esprimono la condizione
necessaria e sufficiente perché si verifichi un'ecclisse solare:
il Sole in congiunzione con la Luna, nel nodo ascendente.
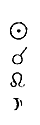
Oltre a ciò il simbolo ![]() inserito tra il Sole e tutti gli altri astri erranti, indica che la serie
rappresenta una congiunzione generale dei Pianeti col Sole; i Pianeti si
trovano nell'ordine: Giove, Saturno, Marte e Mercurio.
inserito tra il Sole e tutti gli altri astri erranti, indica che la serie
rappresenta una congiunzione generale dei Pianeti col Sole; i Pianeti si
trovano nell'ordine: Giove, Saturno, Marte e Mercurio.
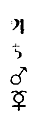
Finalmente gli ultimi tre simboli ci dicono che Mercurio è in opposizione con Venere, aspetto per vero dire non familiare a noi, che parliamo d'opposizione, soltanto quando la Terra giaccia tra due corpi del sistema, allineati con essa. Nel Capo seguente si renderà conto di questa circostanza e si vedrà che la configurazione celeste, rappresentata dalla serie dei simboli, non è già fantastica, ma riproduce un fenomeno reale, predetto ed osservato, e descritto dagli storici dell'epoca.
CAPO III.
La congiunzione
generale del 16 settembre 1186 d. C.
Fonti storiche. - Fu nell'anno 1179 che si diffusero per l'Europa voci disastrose sulle conseguenze di una congiunzione generale, che doveva accadere sette anni dopo, nel mese di settembre, e nella costellazione della Libra; cinque mesi prima della congiunzione si sarebbe verificata anche un'ecclisse solare. La notizia più antica che si conosca intorno a questo fatto ci vien tramandata dal cronista inglese Benedetto Abate (Benedictus Petroburgensis, morto nel 1194); egli riporta il testo (16) di uno dei tanti pronostici che allora correvano per il mondo, dovuto all'astrologo Curumphira, ove questi enumera le calamità naturali e sociali che avrebbero accompagnato l'avvenimento. Benedetto fa seguire al pronostico di Corumphira un' accuratissima elegia, dettata dal monaco vigornese Anselmo, il quale riassume lo spettacolo celeste della congiunzione e dell'ecclisse, nell'esametro:
Nox sine sideribus lunaque dies sine sole.
A questi documenti abbastanza vaghi, un altro cronista inglese contemporaneo, Roger of Hoveden (morto nel 1202), aggiunge nei suoi Annali (17) una vera e propria predizione astronomica del fenomeno, il cui autore è un tal Guglielmo astrologo (18); trascrivo il brano che maggiormente c'interessa:
"Anno ab incarnatione Domini millesimo centesimo octogesimo sexto. Haec autem conjunctio 16 die Septembris erit, feria tertia, hora prima, dominus horae Mars, Sole oriente, et Planetis in locis suis, ut subsequitur. Horoscopus Libra, gradus primus; Sol gradus 30 virginis; Iupiter gradus secundus, minuta 3. Venus gradus 3, minuta 49; Saturnus gradus 8, minuta 6; Mercurius gradus 4, minuta 10; Mars gradus 9, minuta 18; Cauda gradus 18, minuta 23, pars guerrae gradus 15; Luna gradus 17, minuta 8; pars fortunae gradus 19; Secundus Libra, gradus 25; Tertius Scorpius, gradus 24; Quartus Capricornus, gradus primus; Quintus Aquarius, gradus 5; Sextus, Pisces gradus 7; Septimus, Aries gradus primus; etc. ".
Anche Sethus Calvisius (1556-1615) nel suo Opus
Chronologicum (19) dà una notizia succinta della predizione
(tolta dal Hoveden) e, comprendente i dati principali dell'oroscopo, come
pure gli elementi dell'ecclisse parziale di Sole del 21 aprile, che precedette
di cinque mesi la congiunzione. Cenni di minor conto nell'Hottinger (20)
e nel Weidler (21). Degli autori francesi riporta la notizia dell'avvenimento
il contemporaneo Rigord (22), senza tuttavia diffondersi nei particolari
della congiunzione, come i cronisti inglesi. Nulla mi venne fatto di trovare
sull'argomento, nel Muratori (23), e l'unica notizia di storico italiano
si legge in C. C. Scaligero (24). Storici più recenti
quali il Montucla (25) il Bailly (26) il Delambre (27) ne
parlano appena, e l'avvenimento che menò tanto scalpore a' suoi
tempi sembra essere stato dimenticato anche da coloro che ricordano congiunzioni
majores
e
mieores
molto meno caratteristiche, accadute prima e dopo quell'epoca (28).
Calcolo della congiunzione con le Tavole moderne. - La fonte da cui attingiamo i dati numerici della congiunzione è la già ricordata cronaca dell'Hoveden, essendo molto probabile che gli altri scrittori, che citano quei medesimi numeri, abbiano copiato da lui. Con le Tavole di P. V. Neugebauer (29) ho ricalcolato le posizioni del Sole, della Luna, dei Pianeti e del nodo lunare discendente (30), per la data civile del 16 settembre 1186, ad ore 6 antimeridiane. Il testo dice sole oriente, e la congiunzione ebbe luogo il giorno dell'equinozio autunnale, essendo il Sole in 30 Virginis (esattamente: 1790º 37').
Il cronista non dice per quale meridiano valga la predizione, ma trattandosi d'un astrologo inglese, io ammetto che l'ora considerata si riferisca al meridiano di Greenwich.
Ho calcolato il luogo di Mercurio anche con le
Tavole del Le Verrier (31) per assicurarmi che la differenza di 5º
34' non dipenda da errore di calcolo; con le dette Tavole si ottiene un
luogo praticamente identico all'altro; cosa indispensabile del resto, essendo
fondate le Tavole del Neugebauer sugli elementi stessi del Le Verrier.
Nella seguente Tabella VII, confronto i dati del cronista con quelli del
calcolo moderno.
TABELLA VII
Congiunzione generale dell'anno 1186 d.C.
| Numeri | Simboli | 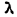 geoc. geoc.
Hoveden |
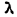 geoc. geoc.
Neugebauer |
Diff.
H-N |
l elioc. | b elioc. | 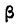 elioc. elioc. |
log r | log  |
| 0 |  |
180º 0' | 179º 37' | + 0º 23' | - | - | - | - | 0,9998 |
| 1 | 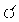 |
- | - | - | - | - | - | - | - |
| 2 | 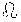 |
198 23 | 194 48 | + 3 35 | - | - | - | - | - |
| 3 | 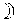 |
197 8 | 197 34 | - 0 26 | - | - | - 0° 19' | - | - |
| 4 | 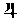 |
182 3 | 181 2 | + 1 1 | 181° 17' | + 1° 21' | + 1 8 | 0,7357 | 0,8091 |
| 5 | 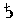 |
188 6 | 185 52 | + 2 14 | 186 30 | + 2 29 | + 2 15 | 0,9875 | 1,0297 |
| 6 | 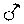 |
189 18 | 189 14 | + 0 4 | 195 14 | + 0 52 | + 0 32 | 0,2034 | 0,4105 |
| 7 | 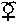 |
184 10 | 189 44 | - 5 34 | 340 39 | - 5 58 | - 3 14 | 9,5605 | 9,8260 |
| 8 | 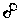 |
- | - | - | - | - | - | - | - |
| 9 | 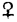 |
183 49 | 184 23 | - 0 34 | 191 0 | + 2 52 | + 1 13 | 9,8582 | 0,2332 |
Quanto all'ammontare delle differenze, bisogna tener presente che le longitudini tramandateci dal cronista non furono già osservate, ma sono dovute al computo anticipato (32) dell'astrologo e soggette quindi ai non lievi errori che si commettevano con le Tavole dell'epoca; non è impossibile che l'astrologo nel comporre la sua predizione, abbia avuto sott'occhio le Tavole marsigliesi (33) pubblicate verso il 1140, da uno che si professa discepolo d'Azarchele; esse costituiscono la prima edizione di tavole astronomiche con commento latino, e non sono altro che una riduzione delle Tavole toledane al meridiano di Marsiglia. Della inesattezza delle Tavole toledane, compilate nel sec. XI, sotto l'impulso e la direzione d'Azarchele, si lamenta sovente l'Anonimo marsigliese, il quale s'accinse alla pubblicazione delle proprie, per metter in grado gli amatori di cose celesti di raggiungere una precisione maggiore, pur dichiarandosi conscio, che qualsiasi Tavola, a lungo andare, non corrisponda più al vero moto degli astri (34).
L'imprecisione dell'effemeridi medioevali è
cosa troppo nota (35) perchè occorra insistervi, anzi dovremmo meravigliarci
che le differenze della Tabella VII sieno relativamente piccole, se la
predizione, come tutto ce lo fa credere, precedette l'avvenimento di parecchi
anni. Disgraziatamente l'oroscopo di Guglielmo astrologo non porta data,
chè altrimenti sarebbe stata questa un'altra occasione per determinare
gli errori in cui s'incorreva a quell'epoca nel computo del luogo dei vari
astri.
Longitudine di Mercurio. Lo scarto massimo
nel computo delle longitudini risulta, com'era prevedibile, nel luogo di
Mercurio, che oggi ancora offre le maggiori difficoltà, e all'osservatore
della sua posizione, e al calcolatore della sua orbita. Se confrontiamo
però la serie dei quattro simboli planetari con le corrispondenti
longitudini geocentriche, calcolate con le Tavole moderne:
| long. | 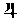 |
= | 181° 2' |
| " | 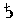 |
= | 185° 52' |
| " | 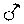 |
= | 189° 14' |
| " | 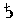 |
= | 189° 44' |
troviamo che i simboli si succedono secondo le longitudini crescenti dei rispettivi astri; Mercurio è dunque al suo posto, cioè: nel momento della congiunzione esso mostrava realmente la longitudine massima nel gruppo dei quattro Pianeti, e gli spettava perciò l'ultimo posto, ove giustamente lo collocò chi formò la serie dei simboli. Costui, per controllare la longitudine pronosticata, poteva aver desunto il luogo del Pianeta dall'osservazione immediata: difatti (per parlare soltanto dell'osservabilità vespertina), verso gli ultimi d'agosto il Pianeta doveva rendersi visibile e restare tale fino all'8 settembre, quando la sua fase raggiunse i 119º; sulle osservazioni d'un'intera settimana era quindi agevole calcolare che il 16 settembre la longitudine geocentrica doveva essere prossimamente 190º, e non 184º, come dal calcolo dell'astrologo Guglielmo.
Se poi non ebbero luogo queste osservazioni di
controllo, si potrà giustificare l'estrazione di Mercurio dal gruppo
dei quattro Pianeti e dal luogo che gli si doveva assegnare per la supposta
longitudine di 184, pensando che al formatore della serie premeva di mettere
in evidenza la peculiare posizione di Venere rispetto a Mercurio e raggruppare
quindi i tre ultimi simboli ![]()
![]()
![]() , ciò che sarebbe stato impossibile, se, in omaggio alla longitudine
pronosticata, lo si fosse confinato tra Giove e Saturno. Io inclino però
a credere alla prima versione, vale a dire: il creatore della serie conobbe
con esattezza la longitudine di Mercurio, molto vicina a 190, ed ebbe la
fortuna di poter mettere in evidenza la circostanza dell'opposizione dei
due pianeti inferiori, senza spostare Mercurio dal rango destinatogli dalle
longitudini.
, ciò che sarebbe stato impossibile, se, in omaggio alla longitudine
pronosticata, lo si fosse confinato tra Giove e Saturno. Io inclino però
a credere alla prima versione, vale a dire: il creatore della serie conobbe
con esattezza la longitudine di Mercurio, molto vicina a 190, ed ebbe la
fortuna di poter mettere in evidenza la circostanza dell'opposizione dei
due pianeti inferiori, senza spostare Mercurio dal rango destinatogli dalle
longitudini.
Opposizione dei Pianeti inferiori nel sistema d'Eraclide Pontico. - Diciamo che due astri erranti sono in opposizione quando la differenza delle loro longitudini ammonta a 180º; ed è implicito che l'osservatore venga a trovarsi nel tempo dell'opposizione tra i due astri, di maniera che, guardando l'uno volge le spalle all'altro e viceversa. Non basta però che l'osservatore risieda nell'interno dell'orbita chiusa di due astri erranti, perchè il loro corso li conduca inevitabilmente, tosto o tardi, ad includere tra loro l'osservatore: l'eccezione è rappresentata appunto da Mercurio e Venere, ed anche i Tolemaici, i quali collocavano la Terra nel centro della circolazione di tutti i Pianeti, non ignoravano che quei due astri non riuscivano a scostarsi mai più che tanto dal Sole e quindi, salvo brevi digressioni ad oriente e ad occidente di esso, erano obbligati ad apparire perpetuamente congiunti.
Ma i partigiani di Eraclide Pontico, che aveva interpretato l'ossequenza al Sole di quei due astri, attribuendo ad essi la qualità di satelliti del Sole e non già di Pianeti della Terra, potevano a buon diritto parlare dell'opposizione di Mercurio rispetto a Venere, ogniqualvolta l'uno dei due si trovava per esempio in quella che noi chiamiamo congiunzione inferiore, e l'altro nella congiunzione superiore, nel quale caso la differenza delle loro longitudini era effettivamente di 180, rispetto al Sole, loro naturale centro di circolazione.
E' noto che il sistema di Eraclide (350 a C.) fu alternativamente accettato e respinto nel mondo astronomico secondo il prevalere dell'una o dell'altra scuola filosofica (36), ma non andò mai dimenticato del tutto. Nell'epoca pretolemaica furono fautori di esso Vitruvio e Teone Smirneo (I sec. d. C.); dopo la pubblicazione dell'opera di Tolomeo, Calcidio (III sec). Più tardi sono annoverati tra i propugnatori di esso Marziano Capella e Macrobio (V sec.), e chi volesse conoscere la fortuna del sistema per tutto il medio evo, non avrebbe da fare altro che leggere il capitolo consacrato dal Duhem a questo argomento, nel II vol. del suo già citato Système du monde. Alla numerosa schiera degli assertori delle idee di Eraclide io penso che appartenesse anche l'ignoto ideatore della serie dei simboli, il quale volle affermare la sua fede nel moto eliocentrico dei pianeti inferiori, inserendo tra questi il simbolo dell'opposizione, che, come abbiamo detto, i Tolemaici avrebbero dovuto rifiutare senz'altro.
Che Venere si trovasse nella congiunzione superiore e Mercurio nell'inferiore, lo si rileva dai rispettivi raggi vettori della Tabella VII; anche Guglielmo astrologo sapeva che Mercurio s'avviava alla congiunzione inferiore, perchè dice esplicitamente nella sua profezia (37): "Mercurius per retrogradationem eam rescindens " etc.; egli non si pronuncia sulla direzione del moto di Venere, ma è inammissibile che l'ideatore della serie, cui noi attribuiamo la capacità di correggere i luoghi del pronostico, abbia d'altra parte ignorato in quale delle due congiunzioni si trovasse allora Venere.
La posizione effettiva degli astri è rappresentata
dalla fig. I; i circoli rappresentano le orbite dei Pianeti superiori ed
inferiori e della Luna; salvo nell'orbita di quest'ultima, fu rispettata
la proporzione delle distanze.
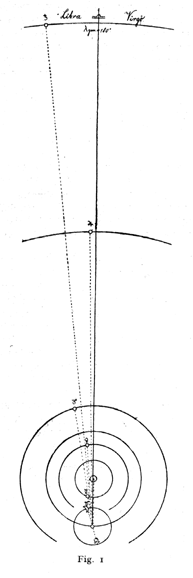
[la stessa figura è visibile più grande]
Dati complementari della predizione. - Guglielmo astrologo aggiunge al quadro del suo pronostico la delimitazione delle case, indicando le cuspidi delle prime sette, con le parole: " Horoscopus Libra, gradus primus... Secundus libra, gradus 25; Tertius Scorpius, gradus 24; Quartus Capricornus, gradus primus; Quintus Aquarius, gradus 5: Sextus Pisces, gradus 7; Septimus Aries, gradus primus (38) " Qui Horoscopus sta per Ascendens (39), vale a dire il punto d'intersezione dello zodiaco con l'orizzonte orientale nel momento considerato; questo punto è secondo l'astrologo nel primo grado della Libra, senza indicazione più precisa. ed io perciò lo ritengo nel punto che noi diremmo di longitudine geocentrica 181º. Quanto alle cuspidi, ossia primi punti delle case, il documento non dice quale domificazione sia stata adottata, e ve ne sono parecchie; cito qui l'enumerazione che ne fa G. Montanari (40): "Hanno voluto alcuni che debba dividersi in 12 parti eguali il Zodiaco con circoli, che passino ad intersecarsi tutti nei Poli dell'istesso Zodiaco; sì che la prima divisione cominci dal punto dell'Oriente, ove esso Zodiaco ascende, ecc... Altri non il Zodiaco ma l'Equatore in dodici parti eguali dividono, e fra questi alcuni lo fanno con circoli che ne' Poli dell'istesso Equatore s'intersecano, altri con circoli che nella comune intersezione del Meridiano con l'orizzonte vanno ad unirsi, altri poscia non l'Equatore, non il Zodiaco ma il Verticale primario dividono in parti eguali, in somma sette, e più, diversi modi sono stati inventati dalla incerta e vagante curiosità degli Astrologi per erigere queste case celesti, così fra loro discordi, ecc. "
La domificazione adottata dal nostro astrologo sembra essere la penultima citata dal Montanari: le case sono contenute entro circoli massimi normali al primo verticale e passano quindi per la linea meridiana dell'osservatore. Il primo dei detti circoli passa per l'Ascendente o cuspide della prima casa; dal punto ove detto circolo taglia l'Equatore s'incomincia a dividere l'Equatore stesso in segmenti di 30º, e mandando per le loro estremità i già menzionati circoli massimi, dall'incontro di questi con l'ecclittica si determinano altrettante cuspidi della seconda, terza, ... dodicesima casa.
Attenendoci dunque a quest'ultima domificazione
e conducendo i circoli massimi per i punti dell'equatore di ascensione
retta: 1º, 31º ... 181º si ottengono sull'ecclittica le
seguenti longitudini geocentriche, accanto alle quali trascrivo le longitudini
somministrate dal documento (fi = 45º; epsilon = 23º 33'):
| Cuspidi | 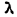 geoc. calcolata geoc. calcolata |
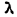 geoc. sec.
Hoveden geoc. sec.
Hoveden |
Diff. |
| Horoscopus | 1° | 1 Librae = 1° | 0 |
| Secundus | 25 | 25 Librae = 25° | 0 |
| Tertius | 54° | 24 Scorpii= 54° | 0 |
| Quartus | 91° | 1 Capricorni = 91° | 0 |
| Quintus | 128° | 5 Aquarii = 125° | 3 |
| Sextus | 157° | 7 Piscium = 157° | 0 |
| Septimus | 181° | 1 Arietis = 181° | 0 |
Salvo la differenza inesplicabile di 3º nella cuspide della quinta casa, l'accordo delle due serie non lascia nulla a desiderare.
Resta che io dica degli altri due simboli astrologici:
Pars
fortunae (41) e Pars guerrae.
La Pars fortunae (cui l'astrologo assegna la long. 19 Librae) è quel punto dello Zodiaco che dista dalla Luna in longitudine, quanto l'Ascendente dista dal Sole, ciò che si esprime con l'equazione:
Pars fortunae 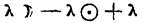 Ascendentis
Ascendentis
Pars fortunae 197º 8' - 179º 37' + 181º = 198º 31'
in accordo col valore dato dal cronista: 19 Librae (42)
La Pars guerrae s'incontra meno frequentemente
nei testi astrologici e il suo concetto variava forse dall'uno all'altro
astrologo; con la definizione che ne dà l'Alcabizio (43):
"
pars guerrae et proeliorum accipitur in die ac nocte a Saturno in Luna
et projicitur ab Ascendente "; non si giunge alla longitudine 15 Librae,
fornita per questo segno dalla predizione.
CAPO IV.
Ora si domanderà: sono i numeri che diedero origine ai simboli, o viceversa, i simboli celesti divennero numeri? Per rispondere a questa domanda dobbiamo riportarci alla fine del sec. XII, quando ebbe luogo la congiunzione, e considerare quale fosse allora la sorte dei numeri; come fu già detto, è fama che i numeri invadessero il continente europeo, provenendo nel sec. XII dalla Spagna islamizzata; ma non se ne riconobbe subito l'utilità, che veniva per così dire annullata dalla instabilità delle loro forme. Queste dovevano esser soggette, prima dell'invenzione della stampa, ai più svariati mutamenti, e perché non tutti potevano aver appreso i numeri dallo stesso manoscritto, e perché ciascuno li avrà modificati secondo la sua maggior o minor capacità d'imitazione ed il suo abito calligrafico, di maniera che, dopo esser passati per innumerevoli mani, dovevano riuscire addirittura irriconoscibili, e dar luogo ad incertezze, ed anche ad imbrogli d'ogni specie. Il Taylor (44) ricorda la proibizione fatta ai banchieri fiorentini, nell'anno 1299, di usare i numeri arabici nella loro contabilità, e la disposizione dello Statuto universitario padovano che imponeva al cartolaio di segnare il prezzo dei libri: non per cifras sed per literas claras. Col tempo tuttavia si sarà veduto che la stupenda invenzione delle cifre, per cui tanto si semplificava ogni calcolo, non era cosa sopprimibile per via di decreti, ma tale piuttosto da meritare che le si agevolasse in tutti i modi il trionfo, e poiché questo trionfo era subordinato all'esistenza d'un paradigma di segni, non già dettati dal capriccio, quali allora dovevano apparire i numeri arabici, ma familiari all'occhio per l'oggetto materiale che rappresentassero, non è impossibile che qualcuno abbia pensato di approfittare della congiunzione generale, fenomeno noto a tutti, se non altro per il terrore che incuteva, proponendo che fosse adottata quale serie crescente dei numeri la successione dei simboli celesti, ordinati secondo la configurazione di quell'ora solenne.
La serie celeste destinata a sostituire le cifre arabiche avrà dovuto vincere da principio l'avversione, oltre che degli Arabi, di tutti quegli spiriti conservatori, che già le usavano in una delle tante forme correnti allora per l'Europa, e dovette accadere che nei nuovi segni qualche elemento labile dei simboli si perdesse, e qualche elemento vitale delle cifre si conservasse, nascendo dalla fusione quella serie definitiva, che serva anc'oggi l'impronta dell'una e dell'altra origine.
Che tutti i popoli nell'accettare le cifre indiane le abbiano deformate un poco secondo segni più familiari, fu già sostenuto da P. Tannery: " ... la tendance naturelle qu'ont eue tous les peuples qui ont adopté les chiffres venues de l'Inde, d'en rapprocher la forme de celle des caractères de leur écriture; cette tendance est trè nettement accusée chez les Arabes et chez les Byzantis; elle doit s'être fait également sentir chez nos ancêtres du Moyen âge " (45).
Quindi, non derivazione di una serie dall'altra, ma riduzione parziale del segno arabico, privo di significato per occhi europei, ad altro segno d'immediata intellegibilità, per la sua somiglianza con oggetti noti. Non diversamente dalle storpiature che subiscono le voci nuove, al loro primo circolare tra il popolo: lo spirito popolare, nell'accettare la parola che non comprende, la modifica di quel tanto che basti farle esprimere un concetto, quasi sempre diversissimo dall'originale, ma, secondo il suo criterio grossolano, proprio e rispondente alla cosa designata.
Bologna, marzo 1925
Osservatorio Astronomico della R. Università.
(1) Cfr. E. CLIVE BAYLEY, On the genealogy
of modern numerals, in Journal of the royal asiatic Soc. of Gr. Br. and
Irl, vol XIV, 335-376, 1882, e vol XV, 1-72, 1883. A pag. 60 (cito
le pagine dell'estratto: pag. I vol. XIV, 335) il Bayley dice che gli Arabi
appresero i numeri indiani nell'anno 773, e che non ne avessero contezza
prima d'allora lo deduce da un editto, emanato dal Califfo Walid (705-715),
il quale nel proibire la lingua greca, in favore dell'arabica, concesse
che si mantenessero per numerali le lettere greche, non avendo la lingua
araba i segni numerali.
(2) Cfr. Is. TAYLOR, The Alphalbet, An account of the origin and development of letters, Londra, 1883, vol. II, pag. 263.
(3) ALBATENII, Opus astronomicum, tradotto ed annotato da C. A. Nallino; Pubbl. R. Oss. Brera, vol. XL, parte 2, praefatio, V. Hoepli, Milano, 1899-1907.
(4) M. CANTOR, Geschichte der Mathematik, I, 708, Lipsia, 1907.
(5) TAYLOR, Inc. cit., voi. lì, 263-264.
(6) Sur l'amulette de Jules Caesar et le cachet de Sepullius Macer, in Revue archeologique, I série, 1846, pag. 258.
(7) Vedi la già citata Nota del LETRONNE, ove ogni segno è discusso separatamente.
(8) Biblioteca nazionale di Parigi, ms. greci, n. 2424.
(9) Memoires scientifiques, tomo IV, 356, Pl. II, Parigi, Gauthier-Villars, 1920.
(10) Cfr. NALLINO, loc. cit., I, 129 (6).
(11) La stessa cosa leggesi nel quadro dei simboli astronomici del GARDTHAUSEN, Griechische Palaeographie, pag. 258, Lipsia, 1879.
(12) Cfr. G. V. SCHIAPARELLI, L'Astronomia nel Vecchio Testamento, pag. 105, fig. 5, Hoepli, Milano, 1903.
(13) J. RUSKA, Griechische Planetendarstellungen in arabischen Steinbuechen, in Stzbr. der Heidelb. Akad. der Wiss. Heidelberg, 1919; 3. Abhandlung.
(14) J. L. FRISCH, De origine characterorum qui apud astronomos planetas significant, in Miscellanea berolinensia, IV, 1734.
(15) Vedi, per esempio: MONTFAUCON, Antiquitates explicatae, II, 170.
(16) Rerum britannicarum medii aevi scriptores: Gesta regis Henrici secundi; edizione curata da W. Stubbs, Londra, 1867; vol. I, pag. 324 e segg. (Rolls Series).
(17) Rerum anglicarum scriptores, Francofurti, 1601, pag. 624 e segg.
(18) Al nome dell'astrologo la cronaca dell'Hoveden non aggiunge altro che le parole clericus Johannes Constabularii Cestriae; le date non si opporrebbero all'ipotesi che quest'astrologo fosse quel Willelmus anglicus (detto anche Massiliensis per essersi egli trasferito dall'Inghilterra a Marsiglia ed avervi passato il rimanente della sua vita), la cui opera Tabula de stellis fixis sec. Azarchelem, fu compiuta nell'anno 1231. Ma all'infuori dell'epoca e dell'omonimia non si ha alcun dato a conferma dell'ipotesi.
(19) Ed. quarta Francoforte s. M., 1650, pag. 781-82.
(20) Historia ecclesiastica, Saec. XII, sect. II, § 3, pag. 198, Hanau, 1656.
(21) Historia astronomiae ecc., pag. 217, Wittemberg, 1741.
(22) Collection des Mémoires relatifs à l'Histoire de France: Vie de Phìlippe Augusee, vol. XI, pag. 43 (trad. dal Guizot).
(23) Rerum italicarum Scriptores, ed. diretta da G. Carducci e V. Fiorini.
(24) Prolegomena all'Astronomicon di M. Manilio, Argentorati, 1655, pag. 9. Noto qui per incidenza che un cenno sommario dell'avvenimento fu dato dal Leopardi quindicenne, nella sua Storia dell'Astronomia, Opere inedite di Giacomo Leopardi, pubblicate da G. Cugnoni, vol. Il, pag. 200-201, Niemeyer, Halle, 1878-80.
(25) Histoire des mathématiques, tomo IV, 374, Parigi, 1802.
(26) Histoire de l'Astronomie ancienne, pag. 137, Parigi, 1781.
(27) Histoire de l'Astronomie du moyen age, pag. 7, Parigi, 1819.
(28) Vedi, per esempio: CIPRIANO LEOVIZIO, De conjunctionibus magnis insignioribus sup. Pl. etc., Marpurgi, 1618.
(29) Tafeln für Sonne, Planeten und Mond, nebst Tafeln der Mondphasen, ecc., Lipsia, 1914.
(30) Nella ristretta area della congiunzione si trovava allora il nodo discendente (cauda draconis), ma nel momento dell'eclisse, cinque mesi prima, la Luna era di conseguenza vicina all'altro nodo, ed è per ciò che nella serie (Tab. VI) troviamo il nodo ascendente.
(31) Ann. Obs. Paris., tomo V, pag. 107 e segg.
(32) Difatti il testo dice "Haec autem conjunctio 16 die septembris erit", etc.
(33) P. DUHEM, Le Système du monde, vol. III, pag. 201, Parigi, 1915.
(34) DUHEM, Ib., pag. 207 e segg.
(35) Vedi a questo proposito: G. B. RICCIOLI, Almagestum novum, Bologna, 1651, vol. I, lib. VII, sect. I, capo VI, pag. 497 e segg.; G. MONTANARI, L'Astrologia convinta di falso, pag. 128, Venezia, 1685; F. ANGELITTI, in G. R. D'ORSOGNA: Dante e l'Almanacco di Profazio giudeo, pag. 41-48, Palermo, 1909.
(36) G. V. SCHIAPARELLI, Origine del sistema eliocentrico presso i Greci, in Mem. R. Ist. lomb. di sc. e lett., vol. XVIII, IX della serie III, fasc. V.
(37) ROGER OF HOVEDEN, loc. cit., pag. 625.
(38) Debbo dire che non intendo bene a quale vocabolo maschile si riferiscano gli ordinali: secundus, tertius etc., Evidentemente l'astrologo accenna alle cuspidi delle case, ma cuspis è femminile, e tale anche domus; nè si può pensare alle voci neutre domicilium o punctum. Esiste la voce paxillus, ma si usa unicamente per indicare le cuspidi delle seguenti quattro case: I, IV, VII, X. (vedi NALLINO, loc. cit., I, 248). Forse va sottinteso circulus.
(39) Il greco oroscopos corrisponde al latino ascendens.
(40) Loc. cit., pag. 92.
(41) NALLINO, loc. cit., 11, pag. 338, 339; ed anche FOMALHAUT, Manuel d'Astrologie sphérique et judiciaire, pag. 84 e segg., Vigot Frères, Parigi, 1897.
(42) Ecco la descrizione che dà l'ALCABIZIO della Pars fortunae: "accipis quidquid est inter solem et lunam et addas super eos gradus ascendentis signi". Libellus ysagogicus etc.: "Differentia quinta in commemoratione universarum partium" Venezia, 1491.
(43) Loc. cit., ibidem.
(44) TAYLOR, loc. cit., II, 263.
(45) Loc. cit., tomo IV, pag. 21.