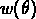 ou
ou 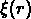 (voir Peebles, 1980).
(voir Peebles, 1980).
L'indicateur statistique le plus répandu est sans aucun doute la fonction
de corrélation à deux points 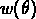 ou
ou 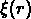 (voir Peebles, 1980).
(voir Peebles, 1980).
La fonction de corrélation angulaire à deux points 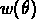 est
définie par la probabilité de trouver des objets dans les angle solides
est
définie par la probabilité de trouver des objets dans les angle solides
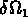 et
et 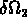 placés à une séparation
placés à une séparation
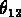 :
:
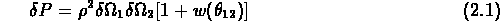
où 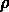 est la densité moyenne des objets dans le ciel.
est la densité moyenne des objets dans le ciel.
A partir des catalogues bidimensionnels on peut obtenir la fonction de
corrélation angulaire 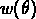 . Dans le cas non-relativiste,
elle satisfait une relation d'échelle:
. Dans le cas non-relativiste,
elle satisfait une relation d'échelle:
où D est la profondeur effective de l'échantillon:
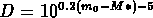 Mpc.
Mpc.
On peut définir en général la probabilité 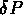 d'avoir un
objet dans
un volume
d'avoir un
objet dans
un volume 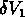 et un autre objet dans un volume
et un autre objet dans un volume 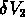 à une distance
à une distance 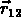 :
:
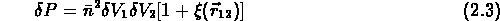
Pour calculer la fonction de corrélation d'une distribution d'objets on utilise en général l'estimateur suivant:
où 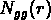 est deux fois le nombre de paires à une séparation r,
est deux fois le nombre de paires à une séparation r,
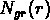 est le nombre d'objets dans un catalogue aléatoire
à une séparation r de la position des objets observés,
est le nombre d'objets dans un catalogue aléatoire
à une séparation r de la position des objets observés,
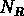 est le nombre total d'objets dans le catalogue aléatoire et
est le nombre total d'objets dans le catalogue aléatoire et
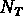 est le nombre d'objets dans le catalogue réel.
On construit un catalogue aléatoire ayant la même forme que le catalogue
de test; on utilise fréquemment
est le nombre d'objets dans le catalogue réel.
On construit un catalogue aléatoire ayant la même forme que le catalogue
de test; on utilise fréquemment 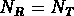 , ce qui signifie que le catalogue
aléatoire a aussi la même densité que le catalogue de test,
et on calcule la valeur moyenne de
, ce qui signifie que le catalogue
aléatoire a aussi la même densité que le catalogue de test,
et on calcule la valeur moyenne de 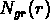 sur plusieurs catalogues
aléatoires.
sur plusieurs catalogues
aléatoires.
L'équation de Limber permet en principe de
trouver la fonction de corrélation spatiale
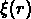 à partir de la fonction de corrélation angulaire
à partir de la fonction de corrélation angulaire
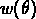 par déprojection,
si l'on connaît la fonction
de luminosité et celle de sélection, mais il est évident qu'une
mesure directe est préferable.
par déprojection,
si l'on connaît la fonction
de luminosité et celle de sélection, mais il est évident qu'une
mesure directe est préferable.
On passe de la fonction de corrélation au spectre de puissance par la transformée de Fourier simple:
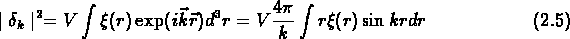
La détermination de la fonction de corrélation 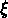 nous donne donc
une information importante;
aux grandes échelles, qui se trouvent en régime linéaire, elle
nous permet, en principe, de connaître le spectre des fluctuations
qui est à l'origine des structures actuelles; inutile de dire qu'aux
grandes échelles la valeur de la fonction de corrélation
est petite et difficile à déterminer.
nous donne donc
une information importante;
aux grandes échelles, qui se trouvent en régime linéaire, elle
nous permet, en principe, de connaître le spectre des fluctuations
qui est à l'origine des structures actuelles; inutile de dire qu'aux
grandes échelles la valeur de la fonction de corrélation
est petite et difficile à déterminer.
De façon analogue, on peut
définir les fonctions de corrélation à N points. Par exemple,
la fonction de corrélation à trois points est définie par l'expression
qui donne la probabilité de trouver un objet dans chacun des trois
volumes 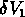 ,
, 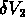 , et
, et 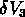 :
:
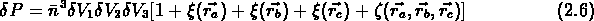
La fonction de corrélation à trois points proprement dite est la quantité
entre crochets, mais on utilise souvent la
fonction de corrélation réduite 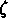 .
.
La description complète d'une distribution est donnée par la
connaissance de toutes les fonctions de corrélation d'ordre
N, 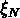 .
.
Si l'on a des objets qui diffèrent entre eux par leur luminosité ou par quelqu' autre paramètre, ou si l'on veut connaître le degré d'association de deux classes d'objets, on utilise la fonction de corrélation croisée, qui est calculée grâce à la formule:

où 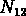 est le nombre de paires formées par un objet du
premier catalogue et un objet du deuxième catalogue qui se
trouvent à une distance r, et
est le nombre de paires formées par un objet du
premier catalogue et un objet du deuxième catalogue qui se
trouvent à une distance r, et 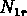 est le nombre de paires
composés par un objet du première catalogue et un objet extrait
d'une distribution aléatoire présentant la même densité que
le deuxième catalogue.
est le nombre de paires
composés par un objet du première catalogue et un objet extrait
d'une distribution aléatoire présentant la même densité que
le deuxième catalogue.