
La fonction de corrélation est en apparence un indicateur très simple, bien défini, qui est directement lié aux prédictions théoriques. Malheureusement, un certain nombre de pièges limitent la significativité des résultats. Je vais présenter ici quelques problèmes existant dans le cadre de la distribution des galaxies; je décrirai les questions liées à la corrélation des amas dans le sixième chapitre.
La fonction de corrélation angulaire à deux points a été mesurée par Groth & Peebles (1977) sur le catalogue de comptages de Lick et, plus récemment, par Maddox et al. (1990) sur le catalogue APM. Ils trouvent

Les deux catalogues ont des profondeurs différentes. Quand on
reporte la 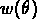 de l'APM à la profondeur du Lick grâce à
la relation (
de l'APM à la profondeur du Lick grâce à
la relation (![]() ), il y a un bon accord jusqu'à
), il y a un bon accord jusqu'à 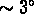 ,
échelle à laquelle la
,
échelle à laquelle la 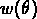 du Lick s'écarte nettement
d'une loi de puissance.
du Lick s'écarte nettement
d'une loi de puissance.
La fonction de corrélation spatiale des galaxies a été mesurée sur le catalogue CfA par Davis & Peebles (1983): ils ont trouvé qu'elle est compatible avec une loi de puissance:

où 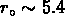
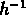 Mpc et
Mpc et 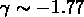 , jusqu'à 10
, jusqu'à 10 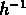 Mpc .
Mpc .
Ces paramètres ont un sens physique si l'on fait l'hypothèse que
l'échantillon étudié est un fair sample de l'Univers, c'est
à dire que ses propriétés statistiques sont représentatives
des propriétés statistiques moyennes de l'Univers; en particulier, il
doit être possible de définir une densité moyenne de l'Univers.
Si l'Univers était un fractal homogène (voir le premier chapitre),
la densité serait une fonction décroissante de l'échelle,
et il serait impossible de définir une densité moyenne; en outre,
il n'y aurait pas d'échelle privilégiée, et la longueur de
corrélation 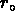 serait simplement proportionnelle à la profondeur
de l'échantillon. C'est ce que certains auteurs ont prétendu mettre en
évidence (voir Coleman & Pietronero, 1992, qui soutiennent cette opinion
dans un article intéressant et ``hérétique") mais, comme on l'a déjà
dit, le comportement des corrélations angulaires, ou l'isotropie du
fond diffus, infirment cette hypothèse.
serait simplement proportionnelle à la profondeur
de l'échantillon. C'est ce que certains auteurs ont prétendu mettre en
évidence (voir Coleman & Pietronero, 1992, qui soutiennent cette opinion
dans un article intéressant et ``hérétique") mais, comme on l'a déjà
dit, le comportement des corrélations angulaires, ou l'isotropie du
fond diffus, infirment cette hypothèse.
Récemment certains auteurs ont prétendu qu'en réalité c'est
la fonction 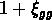 qui suit deux lois de puissance différentes, l'une
aux échelles inférieures à
qui suit deux lois de puissance différentes, l'une
aux échelles inférieures à 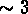
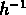 Mpc , l'autre aux échelles
supérieures à
Mpc , l'autre aux échelles
supérieures à 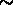 3
3 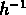 Mpc , avec
Mpc , avec 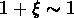 à 35
à 35 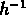 Mpc \
(Guzzo et al., 1991; Calzetti et al., 1992). Ce fait, selon ces auteurs,
indiquerait l'existence de deux régimes, l'un non-linéaire aux petites
échelles,
l'autre linéaire aux plus grandes échelles, reflètant
le spectre de fluctuations primordiales.
Mis à part le problème des erreurs associées et le fait que si
la fonction de corrélation suit une loi de puissance,
Mpc \
(Guzzo et al., 1991; Calzetti et al., 1992). Ce fait, selon ces auteurs,
indiquerait l'existence de deux régimes, l'un non-linéaire aux petites
échelles,
l'autre linéaire aux plus grandes échelles, reflètant
le spectre de fluctuations primordiales.
Mis à part le problème des erreurs associées et le fait que si
la fonction de corrélation suit une loi de puissance, 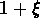 peut être approximée en échelle logarithmique par deux lignes
droites, le problème posé par cette interprétation est
que la géométrie des structures dans un échantillon
affecte la pente de la fonction de corrélation; par exemple un filament donne
peut être approximée en échelle logarithmique par deux lignes
droites, le problème posé par cette interprétation est
que la géométrie des structures dans un échantillon
affecte la pente de la fonction de corrélation; par exemple un filament donne
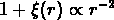 , et une structure plane donne
, et une structure plane donne
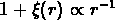 (l'analyse de Guzzo et al.
a été conduite sur le catalogue de Pisces-Perseus, un Superamas
de forme filamentaire).
Dekel & Aarseth (1984), analysant la corrélation du catalogue CfA
(qui contient l'amas de Coma), avaient par ailleurs déjà remarqué
un changement de pente de
(l'analyse de Guzzo et al.
a été conduite sur le catalogue de Pisces-Perseus, un Superamas
de forme filamentaire).
Dekel & Aarseth (1984), analysant la corrélation du catalogue CfA
(qui contient l'amas de Coma), avaient par ailleurs déjà remarqué
un changement de pente de 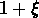 à 3 Mpc
à 3 Mpc 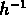 Mpc , qu'ils interprétaient
comme le passage de l'échelle des amas à l'échelle où les
structures planes étaient prédominantes.
Mpc , qu'ils interprétaient
comme le passage de l'échelle des amas à l'échelle où les
structures planes étaient prédominantes.
En outre, le fait que nous ne disposons pas des distances des galaxies, mais de leurs vitesses radiales pose un problème supplémentaire. En présence de vitesses propres très grandes, la distribution tridimensionnelle aura une certaine distortion. Cela est évident dans l'effet dit du ``doigt de Dieu", où la dispersion des vitesses des galaxies dans un amas provoque un étalement des galaxies le long de la ligne de visée. On peut alors calculer séparemment les composantes radiale et projetée de la fonction de corrélation; si la composante radiale est plus grande, cela peut indiquer un effet de distortion.
Une autre complication survient lors de
la normalisation de la fonction de corrélation; le problème peut
être résumé par la question suivante: quelle est la densité
moyenne des galaxies
(ou des amas) dans l'Univers? Il est clair qu'il faudrait connaître la
densité réelle de l'Univers pour pouvoir comparer deux catalogues
différents; pour les galaxies on estime la densité moyenne
à partir de la fonction de luminosité de Schechter, qui est
supposée être universelle, mais par exemple pour les catalogues d'amas,
on doit utiliser la densité estimée du catalogue, 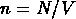 .
L'effet résultant est qu'on peut introduire une anti-corrélation
artificielle à grande échelle. En fait, le nombre total de voisins
d'un objet donné est:
.
L'effet résultant est qu'on peut introduire une anti-corrélation
artificielle à grande échelle. En fait, le nombre total de voisins
d'un objet donné est:
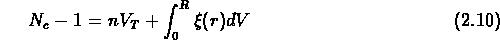
où n est la densité moyenne, 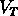 le volume
totale de l'échantillon, et R le rayon qui inclut tout le volume.
le volume
totale de l'échantillon, et R le rayon qui inclut tout le volume.
Si on prend 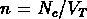 , on a
, on a

ce qui implique qu'à une certaine échelle la 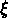 mesurée doit
devenir négative.
mesurée doit
devenir négative.
Dans le cas d'un catalogue limité en magnitude ou en diamètre apparents,
il faut aussi estimer la fonction de sélection des objets.
Dans certains cas
on doit tenir compte d'une sélection inhomogène d'objets en fonction
de la distance zénithale, ou de la déclinaison 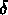 , ou de
la latitude galactique
, ou de
la latitude galactique 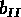 .
Plus généralement, avec une sélection en magnitude apparente (flux) ou
en diamètre apparent on perd de plus en plus d'objets intrinsèquement
moins brillants lorsque l'on augmente la profondeur.
.
Plus généralement, avec une sélection en magnitude apparente (flux) ou
en diamètre apparent on perd de plus en plus d'objets intrinsèquement
moins brillants lorsque l'on augmente la profondeur.
Pour corriger cet effet on peut
tabuler la densité observée en fonction du décalage vers le rouge
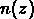 , et distribuer les objets du catalogue aléatoire utilisé pour
calculer
, et distribuer les objets du catalogue aléatoire utilisé pour
calculer 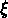 avec une probabilité décroîssante,
suivant le comportement de la densité observée.
Une autre technique consiste à redistribuer les décalages vers le rouge des objets
observés aux objets du catalogue aléatoire, mais
avec un lissage gaussien, pour éviter de reproduire les structures
à petite échelle du catalogue réel.
avec une probabilité décroîssante,
suivant le comportement de la densité observée.
Une autre technique consiste à redistribuer les décalages vers le rouge des objets
observés aux objets du catalogue aléatoire, mais
avec un lissage gaussien, pour éviter de reproduire les structures
à petite échelle du catalogue réel.
L'estimation des erreurs est un autre point fondamental pour la comparaison d'un échantillon avec un autre ou avec la prédiction d'un modèle théorique. Les erreurs poissoniennes sous-estiment l'erreur réelle, car les paires d'objets sur lesquelles on mesure la fonction de corrélation ne sont pas indépendantes. La technique de bootstrap est sans doute plus réaliste: elle utilise le catalogue des objets observés pour générer des pseudo-catalogues dont les objets sont tirés au hasard à partir du catalogue réel.