



Next: Minimal Spanning Tree
Up: Méthodes d'analyse statistique
Previous: Discussion
Cette analyse est basée sur un algorithme dit ``amis des amis":
à partir d'une distribution, on prend un point de la distribution
et on cherche tous les objets qui se trouvent à une distance inférieure
à un rayon r donné; à partir de chaque objet ainsi trouvé,
on répète l'opération de recherche.
Cette technique est très utile, car
il est possible d'identifier de manière objective des familles d'objets,
ou des objets isolés. Elle a été utilisée pour la première fois
pour la recherche de groupes (Turner & Gott, 1977; Materne, 1979).
Le choix du rayon influence évidemment le résultat.
L'analyse de percolation est très simple:
on calcule la distance interparticulaire moyenne
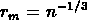 et l'on connecte
tous les objets qui sont séparés par une distance inférieure à
et l'on connecte
tous les objets qui sont séparés par une distance inférieure à
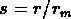 , où l'on fait varier r. Pour chaque s on enregistre la
longueur du plus grand groupe d'objets connectés, et on divise
cette longueur par la dimension typique de l'échantillon
(
, où l'on fait varier r. Pour chaque s on enregistre la
longueur du plus grand groupe d'objets connectés, et on divise
cette longueur par la dimension typique de l'échantillon
(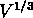 , où V est le volume de l'échantillon). On calcule cette
longueur
, où V est le volume de l'échantillon). On calcule cette
longueur 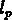 en fonction de s. Quand
en fonction de s. Quand 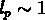 on atteint la
``percolation", c'est à dire que la dimension de la plus grande structure
connectée est comparable à la dimension de l'échantillon total.
Chaque distribution d'objets sera donc
caractérisée par une valeur critique
on atteint la
``percolation", c'est à dire que la dimension de la plus grande structure
connectée est comparable à la dimension de l'échantillon total.
Chaque distribution d'objets sera donc
caractérisée par une valeur critique 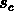 correspondant à
la percolation. Pour une distribution de Poisson avec
un grand nombre de points la percolation est atteinte quand
correspondant à
la percolation. Pour une distribution de Poisson avec
un grand nombre de points la percolation est atteinte quand
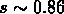 . Si les points sont distribués sur une grille
réguliere, on obtiendra la percolation quand s = 1.
La percolation sera plus facile en présence de plans parallèles
ou de filaments.
La percolation peut être utile pour comparer
des distributions différentes, qui peuvent être des échantillons de
galaxies, ou des distributions résultant de simulations numériques,
et identifier celles qui reproduisent au mieux les observations.
. Si les points sont distribués sur une grille
réguliere, on obtiendra la percolation quand s = 1.
La percolation sera plus facile en présence de plans parallèles
ou de filaments.
La percolation peut être utile pour comparer
des distributions différentes, qui peuvent être des échantillons de
galaxies, ou des distributions résultant de simulations numériques,
et identifier celles qui reproduisent au mieux les observations.
Il est clair que sous la forme
décrite ci-dessus on peut l'appliquer aux catalogues limités
en volume. Mais on peut tenir compte de la fonction de sélection
et appliquer cette technique aussi à un catalogue limité en magnitude,
comme l'on verra dans le chapitre consacré aux groupes de galaxies.
Pourtant cette statistique présente des problèmes qui ont été
analysés par Dekel & West (1985). Ceux-ci trouvent que les propriétés
de percolation de différents modèles de formation de galaxies ne sont
pas très différentes (ils utilisent un code d'Aarseth, 1984, et testent
trois scénarios, bottom-up, top-down -pancake- et un modèle hybride).
Plus grave, les propriétés de percolation
dependent de la densité
moyenne et du volume considéré. Ces problèmes sont moins importants
si l'on considère des catalogues limités en volume et si l'on utilise
les mêmes volumes (c'est à dire avec la même géométrie) et des
densités comparables.
L'algorithme permet également de déterminer
la fonction de multiplicité: cette
fonction représente la fraction d'objets qui se trouvent dans des
systèmes de multiplicité m.
La multiplicité m d'un système est définie de la manière
suivante: si un système est composé de N objets,
alors m est la partie entière de 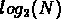 .
Par exemple, un objet isolé a une multiplicité m = 0,
système avec deux ou trois membres a une multiplicité m = 1,
les groupes avec
.
Par exemple, un objet isolé a une multiplicité m = 0,
système avec deux ou trois membres a une multiplicité m = 1,
les groupes avec 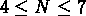 ont multiplicité m = 2, etc...
La fonction de multiplicité nous dit quelle est la distribution
des galaxies ou des amas par classe de richesse,
et répresente un autre test pour comparer observations et simulations.
Elle a été appliquée pour la première fois par Einasto et al. (1984)
à l'analyse du Superamas Local.
Cette définition de la fonction
de multiplicité présente pourtant un défaut important: elle
dépend de la densité d'objets,
et un catalogue plus dense aura ainsi une probabilité plus grande de former
des groupes plus riches.
On peut rémedier à cela en utilisant de nouveaux paramètres
ont multiplicité m = 2, etc...
La fonction de multiplicité nous dit quelle est la distribution
des galaxies ou des amas par classe de richesse,
et répresente un autre test pour comparer observations et simulations.
Elle a été appliquée pour la première fois par Einasto et al. (1984)
à l'analyse du Superamas Local.
Cette définition de la fonction
de multiplicité présente pourtant un défaut important: elle
dépend de la densité d'objets,
et un catalogue plus dense aura ainsi une probabilité plus grande de former
des groupes plus riches.
On peut rémedier à cela en utilisant de nouveaux paramètres
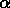 ,
, 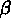 et
et 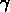 , qui représentent respectivement la fraction d'objets
dans des groupes petits, moyens et grands, définis avec une sous-division
en trois parties égales de la multiplicité maximale
, qui représentent respectivement la fraction d'objets
dans des groupes petits, moyens et grands, définis avec une sous-division
en trois parties égales de la multiplicité maximale
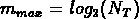 de l'échantillon, où
de l'échantillon, où 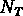 est le nombre total
d'objets (on a
est le nombre total
d'objets (on a 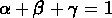 ).
Cette technique a été utilisée par Pellegrini et al. (1990) dans leur
analyse du SSRS, et par Zucca et al. (1991, voir chapitre 4).
).
Cette technique a été utilisée par Pellegrini et al. (1990) dans leur
analyse du SSRS, et par Zucca et al. (1991, voir chapitre 4).




Next: Minimal Spanning Tree
Up: Méthodes d'analyse statistique
Previous: Discussion
alberto cappi
Wed Feb 5 10:43:08 MET 1997
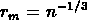 et l'on connecte
tous les objets qui sont séparés par une distance inférieure à
et l'on connecte
tous les objets qui sont séparés par une distance inférieure à
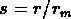 , où l'on fait varier r. Pour chaque s on enregistre la
longueur du plus grand groupe d'objets connectés, et on divise
cette longueur par la dimension typique de l'échantillon
(
, où l'on fait varier r. Pour chaque s on enregistre la
longueur du plus grand groupe d'objets connectés, et on divise
cette longueur par la dimension typique de l'échantillon
(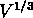 , où V est le volume de l'échantillon). On calcule cette
longueur
, où V est le volume de l'échantillon). On calcule cette
longueur 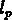 en fonction de s. Quand
en fonction de s. Quand 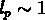 on atteint la
``percolation", c'est à dire que la dimension de la plus grande structure
connectée est comparable à la dimension de l'échantillon total.
Chaque distribution d'objets sera donc
caractérisée par une valeur critique
on atteint la
``percolation", c'est à dire que la dimension de la plus grande structure
connectée est comparable à la dimension de l'échantillon total.
Chaque distribution d'objets sera donc
caractérisée par une valeur critique 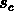 correspondant à
la percolation. Pour une distribution de Poisson avec
un grand nombre de points la percolation est atteinte quand
correspondant à
la percolation. Pour une distribution de Poisson avec
un grand nombre de points la percolation est atteinte quand
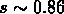 . Si les points sont distribués sur une grille
réguliere, on obtiendra la percolation quand s = 1.
La percolation sera plus facile en présence de plans parallèles
ou de filaments.
La percolation peut être utile pour comparer
des distributions différentes, qui peuvent être des échantillons de
galaxies, ou des distributions résultant de simulations numériques,
et identifier celles qui reproduisent au mieux les observations.
. Si les points sont distribués sur une grille
réguliere, on obtiendra la percolation quand s = 1.
La percolation sera plus facile en présence de plans parallèles
ou de filaments.
La percolation peut être utile pour comparer
des distributions différentes, qui peuvent être des échantillons de
galaxies, ou des distributions résultant de simulations numériques,
et identifier celles qui reproduisent au mieux les observations.
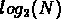 .
Par exemple, un objet isolé a une multiplicité m = 0,
système avec deux ou trois membres a une multiplicité m = 1,
les groupes avec
.
Par exemple, un objet isolé a une multiplicité m = 0,
système avec deux ou trois membres a une multiplicité m = 1,
les groupes avec 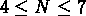 ont multiplicité m = 2, etc...
La fonction de multiplicité nous dit quelle est la distribution
des galaxies ou des amas par classe de richesse,
et répresente un autre test pour comparer observations et simulations.
Elle a été appliquée pour la première fois par Einasto et al. (1984)
à l'analyse du Superamas Local.
Cette définition de la fonction
de multiplicité présente pourtant un défaut important: elle
dépend de la densité d'objets,
et un catalogue plus dense aura ainsi une probabilité plus grande de former
des groupes plus riches.
On peut rémedier à cela en utilisant de nouveaux paramètres
ont multiplicité m = 2, etc...
La fonction de multiplicité nous dit quelle est la distribution
des galaxies ou des amas par classe de richesse,
et répresente un autre test pour comparer observations et simulations.
Elle a été appliquée pour la première fois par Einasto et al. (1984)
à l'analyse du Superamas Local.
Cette définition de la fonction
de multiplicité présente pourtant un défaut important: elle
dépend de la densité d'objets,
et un catalogue plus dense aura ainsi une probabilité plus grande de former
des groupes plus riches.
On peut rémedier à cela en utilisant de nouveaux paramètres
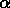 ,
, 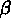 et
et 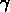 , qui représentent respectivement la fraction d'objets
dans des groupes petits, moyens et grands, définis avec une sous-division
en trois parties égales de la multiplicité maximale
, qui représentent respectivement la fraction d'objets
dans des groupes petits, moyens et grands, définis avec une sous-division
en trois parties égales de la multiplicité maximale
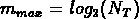 de l'échantillon, où
de l'échantillon, où 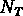 est le nombre total
d'objets (on a
est le nombre total
d'objets (on a 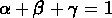 ).
Cette technique a été utilisée par Pellegrini et al. (1990) dans leur
analyse du SSRS, et par Zucca et al. (1991, voir chapitre 4).
).
Cette technique a été utilisée par Pellegrini et al. (1990) dans leur
analyse du SSRS, et par Zucca et al. (1991, voir chapitre 4).