



Next: Probabilité de vides
Up: Méthodes d'analyse statistique
Previous: Les amis des
Le Minimal Spanning Tree (Zahn 1971) est un test statistique derivé
de la théorie des graphes. Les N points d'une distribution sont
connectés par N-1 lignes droites, ou segments (en anglais edges);
cette connexion doit
être de longueur minimale et sans circuit fermé.
Après cette opération, les branches trop longues ou secondaires sont
éliminées, par exemple les segments plus
longs que 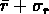 (où
(où 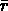 est la valeur moyenne et
est la valeur moyenne et
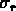 la déviation standard de la distribution des longueurs des
segments) et les branches avec moins d'un nombre minimal fixé de
segments. Cette opération
est évidemment plutôt arbitraire, mais le résultat final donne
une bonne idée des structures filamentaires dans la distribution.
Le point faible est que cette filamentarité n'est pas précisément
quantifiée.
Barrow, Bhavsar & Sonoda (1984; 1985) ont montré
que ce test identifiait avec succès les filaments dans une distribution
de points, et il a été appliqué par Bhavsar & Ling (1988)
à un échantillon extrait du catalogue CfA.
la déviation standard de la distribution des longueurs des
segments) et les branches avec moins d'un nombre minimal fixé de
segments. Cette opération
est évidemment plutôt arbitraire, mais le résultat final donne
une bonne idée des structures filamentaires dans la distribution.
Le point faible est que cette filamentarité n'est pas précisément
quantifiée.
Barrow, Bhavsar & Sonoda (1984; 1985) ont montré
que ce test identifiait avec succès les filaments dans une distribution
de points, et il a été appliqué par Bhavsar & Ling (1988)
à un échantillon extrait du catalogue CfA.
alberto cappi
Wed Feb 5 10:43:08 MET 1997
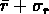 (où
(où 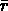 est la valeur moyenne et
est la valeur moyenne et
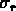 la déviation standard de la distribution des longueurs des
segments) et les branches avec moins d'un nombre minimal fixé de
segments. Cette opération
est évidemment plutôt arbitraire, mais le résultat final donne
une bonne idée des structures filamentaires dans la distribution.
Le point faible est que cette filamentarité n'est pas précisément
quantifiée.
Barrow, Bhavsar & Sonoda (1984; 1985) ont montré
que ce test identifiait avec succès les filaments dans une distribution
de points, et il a été appliqué par Bhavsar & Ling (1988)
à un échantillon extrait du catalogue CfA.
la déviation standard de la distribution des longueurs des
segments) et les branches avec moins d'un nombre minimal fixé de
segments. Cette opération
est évidemment plutôt arbitraire, mais le résultat final donne
une bonne idée des structures filamentaires dans la distribution.
Le point faible est que cette filamentarité n'est pas précisément
quantifiée.
Barrow, Bhavsar & Sonoda (1984; 1985) ont montré
que ce test identifiait avec succès les filaments dans une distribution
de points, et il a été appliqué par Bhavsar & Ling (1988)
à un échantillon extrait du catalogue CfA.