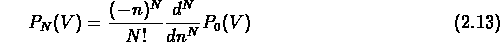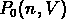 est définie
comme la probabilité qu'une sphère de volume V placée
aléatoirement dans le catalogue, ne contienne pas de galaxies.
White (1979) a montré qu'elle est liée aux fonctions de corrélation à
n points:
est définie
comme la probabilité qu'une sphère de volume V placée
aléatoirement dans le catalogue, ne contienne pas de galaxies.
White (1979) a montré qu'elle est liée aux fonctions de corrélation à
n points:
La distribution des vides peut être analysée suivant une méthode suggerée par Ryden & Turner (1984; Nearest Neighbour Statistics). On construit une grille cubique régulière, de pas égal à la distance interparticulaire moyenne. On étudie ensuite la distribution des distances entre chaque sommet des cubes élémentaires et la galaxie la plus proche.
La fonction de probabilité de vides 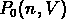 est définie
comme la probabilité qu'une sphère de volume V placée
aléatoirement dans le catalogue, ne contienne pas de galaxies.
White (1979) a montré qu'elle est liée aux fonctions de corrélation à
n points:
est définie
comme la probabilité qu'une sphère de volume V placée
aléatoirement dans le catalogue, ne contienne pas de galaxies.
White (1979) a montré qu'elle est liée aux fonctions de corrélation à
n points:
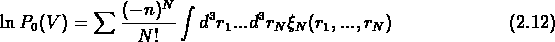
Elle dépend du volume testé et de la densité n du catalogue,
et n'est donc pas très utile dans sa forme la plus simple.
Beaucoup plus intéressante est au contraire la fonction
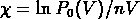 , c'est à dire le logarithme de
, c'est à dire le logarithme de
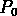 normalisé à
la valeur corréspondant à une distribution poissonienne (
normalisé à
la valeur corréspondant à une distribution poissonienne (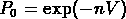 )
de la même densité. Cette quantité exprimée en fonction
de
)
de la même densité. Cette quantité exprimée en fonction
de 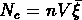 , où
, où 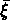 est la fonction de corrélation
moyenne dans un volume V, est indépendante de la densité pour les
distributions à invariance d'échelle , qui seront décrites ensuite.
La distribution des galaxies semble suivre cette invariance d'échelle ,
ainsi que la distribution des amas. Ce fait nous permet des comparer des
catalogues différents, sans problèmes de densité ou de normalisation,
comme c'est le cas pour les fonctions de corrélation.
La probabilité de vides est aussi une fonction génératrice
des probabilités de trouver N objets (White, 1979):
est la fonction de corrélation
moyenne dans un volume V, est indépendante de la densité pour les
distributions à invariance d'échelle , qui seront décrites ensuite.
La distribution des galaxies semble suivre cette invariance d'échelle ,
ainsi que la distribution des amas. Ce fait nous permet des comparer des
catalogues différents, sans problèmes de densité ou de normalisation,
comme c'est le cas pour les fonctions de corrélation.
La probabilité de vides est aussi une fonction génératrice
des probabilités de trouver N objets (White, 1979):