Ce test a été proposé par Gott, Melott et Dickinson (1986; voir aussi Weinberg, 1986): il s'agit d'une statistique qui analyse les surfaces de même densité (ou contraste de densité). On définit le genus d'une surface comme la différence entre le nombre de trous et le nombre de régions isolées qui se trouvent sur la surface. Un tore a un genus égal à l'unité (un trou moins 0 régions isolées). La courbure gaussienne d'une surface bidimensionnelle en un point fixé est l'inverse du produit des deux rayons de courbure principaux au même point:
Grâce au théorème de Gauss-Bonnet, le genus est relié à l'integrale de K sur la surface:
Une distribution gaussienne de contraste de densité
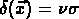a un genus égal à
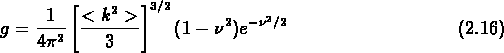
où
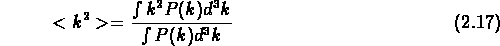
et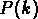 
est le spectre de puissance.
Si l'on suppose une loi de puissance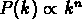 
, convoluée avec
un filtre gaussien, on a:
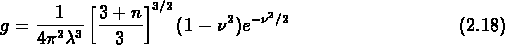
Une distribution gaussienne est donc symétrique du point de vue du genus:
les valeurs positives de 
qui correspondent aux régions pleines,
et les valeurs négatives de 
qui correspondent aux vides, ont
le même genus: on parle dans ce cas d'une topologie en ``éponge".
Une distribution qui montre une courbe de genus tendant vers les valeurs
negatives
de 
est dite avoir une meatball topology, tandis qu'un distribution
avec une courbe plus centrée sur la partie positive des 
est dite
avoir une swiss-cheese topology. Gott et al. (1989) ont
appliqué cette statistique à des échantillons de galaxies et d'amas:
leurs résultats indiquent une topologie ``meatball" aux petites
échelles, et sont compatibles avec une distribution gaussiene aux plus
grandes échelles.