



Next: Analyse multifractale
Up: Méthodes d'analyse statistique
Previous: Analyse topologique: le
Comme je l'ai déjà signalé,
dans un catalogue de galaxies ou d'amas la distance, lorsqu'elle
est calculée à partir du décalage vers le rouge,
est une mesure de vitesse radiale.
Celle-ci correspond à une distance
si les objets suivent le flux d'Hubble et ont donc une vitesse propre
négligeable.
Par exemple, un effet bien visible dans le CfA est l'élongation correspondant
à l'amas de Coma, qui ne correpond pas à une vraie élongation dans
l'espace mais qui est une conséquence de la dispersion de vitesse de l'amas
(effet finger of God). En ce qui concerne les amas,
Bahcall et al. (1986) avaient trouvé une anisotropie entre séparation
radiale et séparation angulaire des amas (exprimées
en 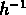 Mpc ), qu'ils ont interpreté comme des mouvements propres des amas
de l'ordre de 2000 km/s.
Mais ce résultat n'a pas été confirmé: en fait,
on peut bien avoir des superamas (du type Corona Borealis)
plus ou moins alignés suivant la direction
radiale, et des effets de projection pourraient être également à l'origine
d'une certaine anisotropie.
L'évidence actuelle est que les amas
de galaxies présentent des vitesses propres
Mpc ), qu'ils ont interpreté comme des mouvements propres des amas
de l'ordre de 2000 km/s.
Mais ce résultat n'a pas été confirmé: en fait,
on peut bien avoir des superamas (du type Corona Borealis)
plus ou moins alignés suivant la direction
radiale, et des effets de projection pourraient être également à l'origine
d'une certaine anisotropie.
L'évidence actuelle est que les amas
de galaxies présentent des vitesses propres 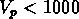 km/s
(voir Postman et al., 1986; et
nous mêmes avons vérifié cette limite grâce à l'existence d'un plan
fondamental pour les amas, qui sera discuté ensuite).
km/s
(voir Postman et al., 1986; et
nous mêmes avons vérifié cette limite grâce à l'existence d'un plan
fondamental pour les amas, qui sera discuté ensuite).
Plusieurs tests permettent de vérifier la présence d'élongations
dans les structures observées.
On peut par exemple effectuer des mesures séparées des deux
composantes de la fonction de corrélation, en fonction l'une de la
séparation angulaire, l'autre de la séparation radiale.
On peut aussi étudier la distribution des valeurs de l'angle 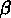 entre la ligne qui connecte une paire et la ligne de visée,
ou de l'angle
entre la ligne qui connecte une paire et la ligne de visée,
ou de l'angle 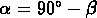 formé avec le plan du ciel--
en fonction de la séparation spatiale des objets.
Le test a été proposé par
Sargent & Turner (1977); il a été par exemple utilisé par
Postman et al. (1992), qui n'ont pas trouvé d'élongation
significative dans leur échantillon statistique d'amas
de galaxies.
formé avec le plan du ciel--
en fonction de la séparation spatiale des objets.
Le test a été proposé par
Sargent & Turner (1977); il a été par exemple utilisé par
Postman et al. (1992), qui n'ont pas trouvé d'élongation
significative dans leur échantillon statistique d'amas
de galaxies.
Si l'on mesure 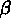 au point médian
de la séparation projetée de la paire, on a:
au point médian
de la séparation projetée de la paire, on a:
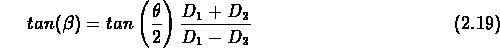
où 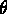 est la séparation angulaire
des deux objets, et
est la séparation angulaire
des deux objets, et
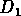 et
et 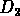 sont leurs distances respectives (
sont leurs distances respectives (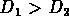 );
);
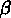 est toujours
est toujours 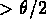 . Cette formule
(Cappi & Maurogordato, 1992) diffère légèrement de celle de Sargent et
Turner, qui ont mesuré
. Cette formule
(Cappi & Maurogordato, 1992) diffère légèrement de celle de Sargent et
Turner, qui ont mesuré 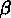 au point médian de la
séparation spatiale, et non projetée, de la paire.
au point médian de la
séparation spatiale, et non projetée, de la paire.
Il faut éliminer toutes les paires dont la distance aux limites
de l'échantillon est inférieure à leur séparation, pour éviter
un biais dans la direction de la ligne de visée.
La valeur moyenne de 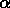 attendue pour une distribution
isotrope est
attendue pour une distribution
isotrope est 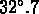 .
.




Next: Analyse multifractale
Up: Méthodes d'analyse statistique
Previous: Analyse topologique: le
alberto cappi
Wed Feb 5 10:43:08 MET 1997
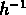 Mpc ), qu'ils ont interpreté comme des mouvements propres des amas
de l'ordre de 2000 km/s.
Mais ce résultat n'a pas été confirmé: en fait,
on peut bien avoir des superamas (du type Corona Borealis)
plus ou moins alignés suivant la direction
radiale, et des effets de projection pourraient être également à l'origine
d'une certaine anisotropie.
L'évidence actuelle est que les amas
de galaxies présentent des vitesses propres
Mpc ), qu'ils ont interpreté comme des mouvements propres des amas
de l'ordre de 2000 km/s.
Mais ce résultat n'a pas été confirmé: en fait,
on peut bien avoir des superamas (du type Corona Borealis)
plus ou moins alignés suivant la direction
radiale, et des effets de projection pourraient être également à l'origine
d'une certaine anisotropie.
L'évidence actuelle est que les amas
de galaxies présentent des vitesses propres 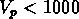 km/s
(voir Postman et al., 1986; et
nous mêmes avons vérifié cette limite grâce à l'existence d'un plan
fondamental pour les amas, qui sera discuté ensuite).
km/s
(voir Postman et al., 1986; et
nous mêmes avons vérifié cette limite grâce à l'existence d'un plan
fondamental pour les amas, qui sera discuté ensuite).
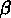 entre la ligne qui connecte une paire et la ligne de visée,
ou de l'angle
entre la ligne qui connecte une paire et la ligne de visée,
ou de l'angle 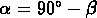 formé avec le plan du ciel--
en fonction de la séparation spatiale des objets.
Le test a été proposé par
Sargent & Turner (1977); il a été par exemple utilisé par
Postman et al. (1992), qui n'ont pas trouvé d'élongation
significative dans leur échantillon statistique d'amas
de galaxies.
formé avec le plan du ciel--
en fonction de la séparation spatiale des objets.
Le test a été proposé par
Sargent & Turner (1977); il a été par exemple utilisé par
Postman et al. (1992), qui n'ont pas trouvé d'élongation
significative dans leur échantillon statistique d'amas
de galaxies.
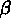 au point médian
de la séparation projetée de la paire, on a:
au point médian
de la séparation projetée de la paire, on a:
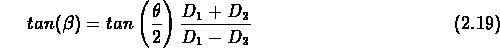
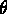 est la séparation angulaire
des deux objets, et
est la séparation angulaire
des deux objets, et
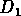 et
et 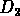 sont leurs distances respectives (
sont leurs distances respectives (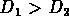 );
);
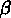 est toujours
est toujours 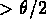 . Cette formule
(Cappi & Maurogordato, 1992) diffère légèrement de celle de Sargent et
Turner, qui ont mesuré
. Cette formule
(Cappi & Maurogordato, 1992) diffère légèrement de celle de Sargent et
Turner, qui ont mesuré 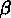 au point médian de la
séparation spatiale, et non projetée, de la paire.
au point médian de la
séparation spatiale, et non projetée, de la paire.
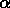 attendue pour une distribution
isotrope est
attendue pour une distribution
isotrope est 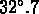 .
.