



Next: Modèles de la
Up: Méthodes d'analyse statistique
Previous: Elongation des structures
La notion de fractal (Mandelbrot, 1982) est liée à la définition de
dimension.
Une mesure d'une distribution non fractale est donné par
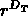 , où
, où 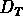 est sa dimension topologique.
Une distribution fractale aura toujours une dimension topologique nulle ou
infinie, donc il faut recourir à une généralisation du concept de mesure,
qui sera donnée par exemple par
est sa dimension topologique.
Une distribution fractale aura toujours une dimension topologique nulle ou
infinie, donc il faut recourir à une généralisation du concept de mesure,
qui sera donnée par exemple par 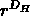 , où
, où 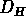 est la dimension
de Hausdorff-Besicovich, et qui donne aussi la définition de fractal.
Un fractal est donc un objet mathématique dont la dimension fractale
(d'Hausdorff)
est la dimension
de Hausdorff-Besicovich, et qui donne aussi la définition de fractal.
Un fractal est donc un objet mathématique dont la dimension fractale
(d'Hausdorff) 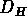 est strictement plus grande que sa dimension topologique
est strictement plus grande que sa dimension topologique
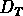 .
Il y a beaucoup de définitions de dimension,
et elles ne coïncident pas nécessairement.
Par exemple, en plus de la dimension d'Hausdorff
.
Il y a beaucoup de définitions de dimension,
et elles ne coïncident pas nécessairement.
Par exemple, en plus de la dimension d'Hausdorff 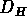 et de la
dimension topologique
et de la
dimension topologique 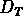 , il faut mentionner
la dimension de corrélation
, il faut mentionner
la dimension de corrélation 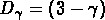 et
la ``capacity dimension"
et
la ``capacity dimension" 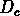 .
.
Une estimation de la dimension de Hausdorff est en effet donnée
par la ``capacity dimension", mais on a toujours  :
on peut calculer
:
on peut calculer 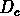 pour un catalogue d'objets
à partir des comptages dans des cellules ou avec le MST.
pour un catalogue d'objets
à partir des comptages dans des cellules ou avec le MST.
Si on considère une distribution de N objets, et 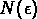 celles
de la même taille
celles
de la même taille  qui recouvrent l'ensemble, la probabilité
de trouver
qui recouvrent l'ensemble, la probabilité
de trouver 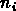 objets dans la celle
i est
objets dans la celle
i est 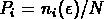 : on dit que
: on dit que 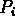 est la mesure associée à la cellule i.
Les dimensions de Renyi (Renyi 1970) sont alors données par:
est la mesure associée à la cellule i.
Les dimensions de Renyi (Renyi 1970) sont alors données par:
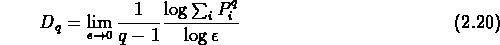
où 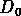 est la capacity dimension et
est la capacity dimension et

Les régions de haute densité ont un plus grand poids quand q > 0,
et les régions sous-denses pèsent davantage quand q < 0.
Une description alternative est donnée par le spectre des singularités
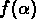 (Halsey et al., 1986).
On peut considérer une structure multifractale comme une superposition
de structures monofractales homogènes.
Supposons que la probabilité
(Halsey et al., 1986).
On peut considérer une structure multifractale comme une superposition
de structures monofractales homogènes.
Supposons que la probabilité 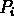 qu'une cellule soit occupée
suit la loi de puissance
qu'une cellule soit occupée
suit la loi de puissance
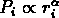 ;
; 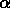 représente la dimension ponctuelle.
Considérons l'ensemble
représente la dimension ponctuelle.
Considérons l'ensemble 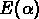 qui contient toutes les
particules qui ont des indices dans l'intervalle
qui contient toutes les
particules qui ont des indices dans l'intervalle 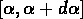 .
On définit
.
On définit 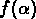 (appelé spectre des singularités)
comme la dimension fractale de l'ensemble
(appelé spectre des singularités)
comme la dimension fractale de l'ensemble 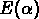 ,
qui est une structure monofractale.
Les paires
,
qui est une structure monofractale.
Les paires 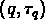 et
et 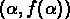 sont liés par la
transformée de Legendre
sont liés par la
transformée de Legendre 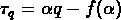 et
et
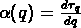 .
Pour une structure multifractale les dimensions
.
Pour une structure multifractale les dimensions
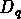 sont des fonctions décroissantes de q, et
sont des fonctions décroissantes de q, et
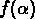 est une fonction convexe, avec une valeur maximale
qui corréspond à la dimension d'Hausdorff
est une fonction convexe, avec une valeur maximale
qui corréspond à la dimension d'Hausdorff 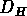 .
.
Certaines propriétés d'invariance d'échelle de la distribution des
galaxies, de la loi de puissance suivie par sa
fonction de corrélation, à l'éventuelle croissance de 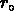 avec la profondeur des échantillons, sont caractéristiques des
fractals.
Il a été suggeré que la distribution des galaxies puisse être un
monofractal (Pietronero, 1987). En fait, la fonction de corrélation peut
alors être réecrite de la manière suivante:
avec la profondeur des échantillons, sont caractéristiques des
fractals.
Il a été suggeré que la distribution des galaxies puisse être un
monofractal (Pietronero, 1987). En fait, la fonction de corrélation peut
alors être réecrite de la manière suivante:
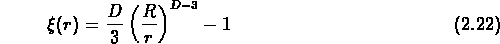
où R est la profondeur de l'échantillon, et l'on voit
que 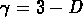 , et que
, et que 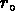 dépend de R.
Cela impliquerait l'impossibilité de définir une densité
moyenne pour l'Univers, et l'abandon des modèles
cosmologiques standard. Mais cette hypothèse
est en désaccord avec les observations,
par exemple avec le comportement de la fonction de corrélation
angulaire en fonction de la profondeur de l'échantillon
(voir Jones et al., 1988; Martínez et Jones, 1990).
dépend de R.
Cela impliquerait l'impossibilité de définir une densité
moyenne pour l'Univers, et l'abandon des modèles
cosmologiques standard. Mais cette hypothèse
est en désaccord avec les observations,
par exemple avec le comportement de la fonction de corrélation
angulaire en fonction de la profondeur de l'échantillon
(voir Jones et al., 1988; Martínez et Jones, 1990).
Pour les galaxies, une description en termes de bifractals
(Balian & Schaeffer, 1989b, qui trouvent deux dimensions,
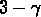 pour les région denses et
pour les région denses et 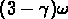 pour les régions
moins denses, où
pour les régions
moins denses, où 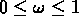 ), dans un intervalle d'échelles
limité, semble être en bon accord avec les observations.
), dans un intervalle d'échelles
limité, semble être en bon accord avec les observations.
Les amas de galaxies semblent aussi montrer des propriétés multifractales
(Borgani, Plionis & Valdarnini, 1992).
Pourtant les catalogues disponibles ne sont pas encore assez grands pour
pouvoir en tirer des conclusions définitives. En plus, la liaison entre
dynamique et développement d'une distribution multifractale n'est pas
claire;
supposant que cette relation soit clarifiée, il faudra
voir si les conditions gaussiennes initiales peuvent générer à
l'époque actuelle une telle distribution, caractérisée par un haut
degré de non-gaussianité.




Next: Modèles de la
Up: Méthodes d'analyse statistique
Previous: Elongation des structures
alberto cappi
Wed Feb 5 10:43:08 MET 1997
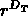 , où
, où 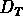 est sa dimension topologique.
Une distribution fractale aura toujours une dimension topologique nulle ou
infinie, donc il faut recourir à une généralisation du concept de mesure,
qui sera donnée par exemple par
est sa dimension topologique.
Une distribution fractale aura toujours une dimension topologique nulle ou
infinie, donc il faut recourir à une généralisation du concept de mesure,
qui sera donnée par exemple par 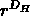 , où
, où 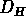 est la dimension
de Hausdorff-Besicovich, et qui donne aussi la définition de fractal.
Un fractal est donc un objet mathématique dont la dimension fractale
(d'Hausdorff)
est la dimension
de Hausdorff-Besicovich, et qui donne aussi la définition de fractal.
Un fractal est donc un objet mathématique dont la dimension fractale
(d'Hausdorff) 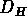 est strictement plus grande que sa dimension topologique
est strictement plus grande que sa dimension topologique
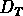 .
Il y a beaucoup de définitions de dimension,
et elles ne coïncident pas nécessairement.
Par exemple, en plus de la dimension d'Hausdorff
.
Il y a beaucoup de définitions de dimension,
et elles ne coïncident pas nécessairement.
Par exemple, en plus de la dimension d'Hausdorff 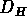 et de la
dimension topologique
et de la
dimension topologique 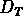 , il faut mentionner
la dimension de corrélation
, il faut mentionner
la dimension de corrélation 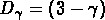 et
la ``capacity dimension"
et
la ``capacity dimension" 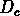 .
.
 :
on peut calculer
:
on peut calculer 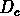 pour un catalogue d'objets
à partir des comptages dans des cellules ou avec le MST.
pour un catalogue d'objets
à partir des comptages dans des cellules ou avec le MST.
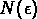 celles
de la même taille
celles
de la même taille  qui recouvrent l'ensemble, la probabilité
de trouver
qui recouvrent l'ensemble, la probabilité
de trouver 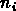 objets dans la celle
i est
objets dans la celle
i est 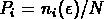 : on dit que
: on dit que 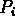 est la mesure associée à la cellule i.
Les dimensions de Renyi (Renyi 1970) sont alors données par:
est la mesure associée à la cellule i.
Les dimensions de Renyi (Renyi 1970) sont alors données par:
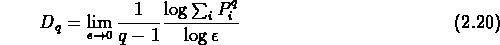
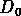 est la capacity dimension et
est la capacity dimension et

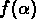 (Halsey et al., 1986).
On peut considérer une structure multifractale comme une superposition
de structures monofractales homogènes.
Supposons que la probabilité
(Halsey et al., 1986).
On peut considérer une structure multifractale comme une superposition
de structures monofractales homogènes.
Supposons que la probabilité 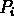 qu'une cellule soit occupée
suit la loi de puissance
qu'une cellule soit occupée
suit la loi de puissance
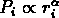 ;
; 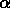 représente la dimension ponctuelle.
Considérons l'ensemble
représente la dimension ponctuelle.
Considérons l'ensemble 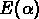 qui contient toutes les
particules qui ont des indices dans l'intervalle
qui contient toutes les
particules qui ont des indices dans l'intervalle 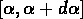 .
On définit
.
On définit 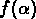 (appelé spectre des singularités)
comme la dimension fractale de l'ensemble
(appelé spectre des singularités)
comme la dimension fractale de l'ensemble 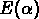 ,
qui est une structure monofractale.
Les paires
,
qui est une structure monofractale.
Les paires 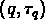 et
et 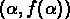 sont liés par la
transformée de Legendre
sont liés par la
transformée de Legendre 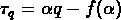 et
et
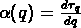 .
Pour une structure multifractale les dimensions
.
Pour une structure multifractale les dimensions
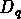 sont des fonctions décroissantes de q, et
sont des fonctions décroissantes de q, et
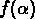 est une fonction convexe, avec une valeur maximale
qui corréspond à la dimension d'Hausdorff
est une fonction convexe, avec une valeur maximale
qui corréspond à la dimension d'Hausdorff 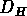 .
.
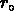 avec la profondeur des échantillons, sont caractéristiques des
fractals.
Il a été suggeré que la distribution des galaxies puisse être un
monofractal (Pietronero, 1987). En fait, la fonction de corrélation peut
alors être réecrite de la manière suivante:
avec la profondeur des échantillons, sont caractéristiques des
fractals.
Il a été suggeré que la distribution des galaxies puisse être un
monofractal (Pietronero, 1987). En fait, la fonction de corrélation peut
alors être réecrite de la manière suivante:
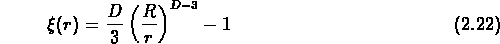
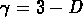 , et que
, et que 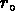 dépend de R.
Cela impliquerait l'impossibilité de définir une densité
moyenne pour l'Univers, et l'abandon des modèles
cosmologiques standard. Mais cette hypothèse
est en désaccord avec les observations,
par exemple avec le comportement de la fonction de corrélation
angulaire en fonction de la profondeur de l'échantillon
(voir Jones et al., 1988; Martínez et Jones, 1990).
dépend de R.
Cela impliquerait l'impossibilité de définir une densité
moyenne pour l'Univers, et l'abandon des modèles
cosmologiques standard. Mais cette hypothèse
est en désaccord avec les observations,
par exemple avec le comportement de la fonction de corrélation
angulaire en fonction de la profondeur de l'échantillon
(voir Jones et al., 1988; Martínez et Jones, 1990).
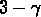 pour les région denses et
pour les région denses et 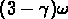 pour les régions
moins denses, où
pour les régions
moins denses, où 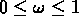 ), dans un intervalle d'échelles
limité, semble être en bon accord avec les observations.
), dans un intervalle d'échelles
limité, semble être en bon accord avec les observations.