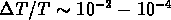Le procédé que je vais décrire est connu sous le nom de
tesselation de Voronoi.
Etant donnée une distribution de points dans l'espace,
on suppose que chaque point est le centre d'une sphère en expansion
uniforme, et que cette expansion commence en même temps et avec la même
vitesse pour tous les points. Les sphères s'intersecteront alors
suivant des plans qui séparent orthogonalement
en sa moitié la ligne qui relie les deux centres d'expansion (dits aussi
noyaux).
Ces plans s'intersectent en des lignes, et les lignes s'intersectent à
leur fois en des points.
Le résultat est ce qu'on appelle une ``mousse" de Voronoi
( Voronoi foam).
Icke & van de Weygaert (1987, 1989) ont essayé de donner une
interprétation physique de cette distribution, en l'associant à
la théorie des explosions (Ikeuchi, 1981; Ostriker et Cowie, 1981).
Si l'on identifie les points d'intersection avec les amas de galaxies,
on obtient une fonction de corrélation comparable à celle observée.
Icke a aussi montré que les légères asphericités initiales des vides
diminuent pendant leur expansion ( Bubble Theorem, Icke, 1984).
Une telle distribution pourrait bien expliquer la présence
de structures périodiques dans la distribution des galaxies.
Mais il n'est pas clair qu'elle constitue une approximation raisonnable
de la réalité du point de vue dynamique.
En plus, il y a une incertitude liée au fait que
la distribution initiale des noyaux (s'ils sont corrélés ou non)
influence évidemment le résultat.
Finalement, le CMB pose un problème sérieux; l'évolution
cinématique d'une distribution de Voronoi impliquerait des fluctuations de
l'ordre de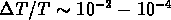 
, en désaccord total avec
les observations de COBE (Coles & Barrow, 1990; Icke & van de Weygaert, 1991).