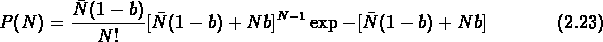
Saslaw & Hamilton (1984) ont calculé dans le cadre de la théorie thermodynamique, appliquée à un systeme homogène autogravitant en équilibre, la probabilité de trouver N objets dans un volume V:
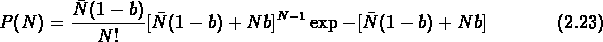
où N = nV et
est le rapport entre l'énergie gravitationnelle de
corrélation W et l'énergie cinetique
.
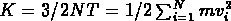Les premiers moments de la distributions sont très simples:
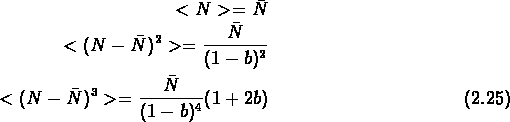
On a:
En particulier, la probabilité de vides est donnée par:
et l'on trouve une loi d'invariance d'échelle pour les vides (Fry, 1986a):
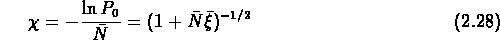
Puisque les observations nous disent que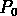 
varie avec l'échelle,
b aussi doit varier. Le problème posé par la distribution
thermodynamique est qu'à chaque échelle on trouve une valeur
differente pour b, tandis que la prédiction théorique requiert que
b soit constant; même chose si l'on veut reproduire un comportement
hiérarchique.
La formule (
) a été derivée pour un clustering
gravitationnel en conditions de quasi-equilibre dans un univers en
expansion, où b est fonction du temps et de l'échelle.
Elle marche bien pour les petites valeurs de N, mais elle ne reproduit pas
les comptages ni théoriques ni observés pour les grands N
(Bouchet et al., 1991).
