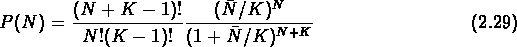
Cette statistique, dite aussi de Bose-Einstein modifiée, qui a été utilisée pour décrire la distribution de multiplicité des hadrons, a été introduite dans le contexte cosmologique par Carruthers et Minh (1983; voir aussi Carruthers, 1991) pour décrire les comptages dans des cellules des amas de galaxies dans le catalogue de Zwicky.
La probabilité de comptage de la distribution binomiale est:
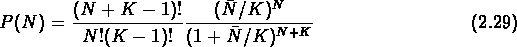
Elle a un comportement hiérarchique si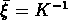 
.
La probabilité de vides , 
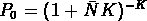donne ainsi
la relation d'échelle:
Figure: Probabilités de vides en fonction de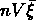 
.
Trait continu: ``minimal model" (Fry, 1986),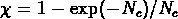 
;
trait interrompu: ``negative binomial" (Carruthers & Smith, 1983),
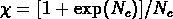; trait pointillé: distribution thermodynamique
(Saslow & Hamilton, 1984),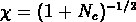 
La figure 
montre
les probabilités de vides des distributions considérées.