



Next: Une analyse des
Up: Groupes de galaxies
Previous: Galaxies d'IRAS et
Puisque l'on dispose de catalogues de groupes, il est naturel de se demander
quelle est leur distribution et quelle est la distribution qu'on
s'attendrait de la théorie.
Une constatation s'impose: les catalogues dont nous disposons sont
pour l'instant trop petits pour permettre d'appliquer d'autres
statistiques que la fonction de corrélation.
Kashlinsky (1987) a combiné la théorie du clustering gravitationnel
(Press et Schechter, 1974) à la théorie de la formation biaisée de
Kaiser (1984), pour faire
des prédictions sur les fonctions de corrélation
de systèmes de masses différentes.
Dans ce cadre, les structures se forment hiérarchiquement
sous l'action de la gravité. Dans une région sur-dense l'expansion de
l'Univers est ralentie, jusqu'au moment où elle s'arrête: c'est le moment
où la structure se ``sépare" de l'Univers en expansion et où
l'effondrement commence: en anglais, on parle de turnaround.
Dans un univers
hiérarchique, la masse caractéristique du turnaround est une
fonction croîssante du temps t.
Kashlinsky a estimé qu'aux échelles inférieures à 10 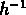 Mpc
(où les fluctuations ne sont pas linéaires) la fonction de corrélation
des amas devrait être égale à celle des galaxies;
en plus, les groupes comprenant plus de 8-10
membres (qui devraient représenter le système le plus commun
de la hiérarchie gravitationnelle actuelle, avec une masse
Mpc
(où les fluctuations ne sont pas linéaires) la fonction de corrélation
des amas devrait être égale à celle des galaxies;
en plus, les groupes comprenant plus de 8-10
membres (qui devraient représenter le système le plus commun
de la hiérarchie gravitationnelle actuelle, avec une masse
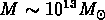 qui correspond à la masse de turnaround)
devraient avoir eux aussi une fonction de
corrélation identique à celle des galaxies.
Aux échelles dépassant celle de turnaround (
qui correspond à la masse de turnaround)
devraient avoir eux aussi une fonction de
corrélation identique à celle des galaxies.
Aux échelles dépassant celle de turnaround (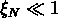 , où
, où
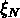 est la fonction d'autocorrélation de masse de la
distribution de masse primordiale), Kashlinsky arrive aux résultats suivants:
est la fonction d'autocorrélation de masse de la
distribution de masse primordiale), Kashlinsky arrive aux résultats suivants:

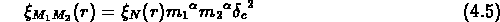

où 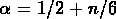 (voir le premier chapitre),
(voir le premier chapitre),
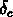 est le contraste de densité
critique
est le contraste de densité
critique 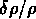 pour le turnaround,
et
pour le turnaround,
et 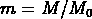 est le rapport entre la masse du système et la masse qui
correspond au turnaround.
La raison physique de la différence entre la relation
(
est le rapport entre la masse du système et la masse qui
correspond au turnaround.
La raison physique de la différence entre la relation
( ) pour les galaxies
et la relation (
) pour les galaxies
et la relation ( ) pour les systèmes de plusieurs galaxies,
est que les galaxies, qui sont passées évidemment par un
processus dissipatif, conservent leur identité
dans des hiérarchies plus grandes, tandis que les systèmes de
galaxies perdent leur identité lorsqu'ils se regroupent.
) pour les systèmes de plusieurs galaxies,
est que les galaxies, qui sont passées évidemment par un
processus dissipatif, conservent leur identité
dans des hiérarchies plus grandes, tandis que les systèmes de
galaxies perdent leur identité lorsqu'ils se regroupent.
La comparaison de ces prédictions avec les observations est
difficile, en particulier aux grandes échelles
impliquées.
Jing & Zhang (1988)
ont utilisé un vieux catalogue de groupes du catalogue CfA
(Geller & Huchra, 1983) et ils ont trouvé qu'aux échelles
supérieures à 10-20 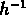 Mpc l'amplitude de la fonction
de corrélation angulaire et spatiale des groupes est
la moitié de celle des galaxies.
Mpc l'amplitude de la fonction
de corrélation angulaire et spatiale des groupes est
la moitié de celle des galaxies.
La fonction de corrélation des
groupes
du CfA et du SSRS a été calculée
respectivement par Ramella et al. (1990; RGH90) et Maia & da Costa
(1990; MDC90).
Maia et da Costa (1989) analysent l'échantillon de groupes
extraits du SSRS, et trouvent que la fonction de
corrélation 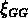 de leurs groupes a une amplitude 2.5
fois plus faible que celle des galaxies.
Il faut souligner que le résultats de Jing & Zhang et de Maia et da Costa
se refèrent à des échelles différentes.
En effet, Maia et da Costa observent justement que leur résultat
ne peut pas être comparé aux prévisions du modèle de
Kashlinsky, simplement parce qu'ils ne peuvent mesurer la
fonction de corrélation qu'aux échelles inférieures à
10
de leurs groupes a une amplitude 2.5
fois plus faible que celle des galaxies.
Il faut souligner que le résultats de Jing & Zhang et de Maia et da Costa
se refèrent à des échelles différentes.
En effet, Maia et da Costa observent justement que leur résultat
ne peut pas être comparé aux prévisions du modèle de
Kashlinsky, simplement parce qu'ils ne peuvent mesurer la
fonction de corrélation qu'aux échelles inférieures à
10 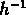 Mpc .
Mpc .
Jing et Zhang, au contraire, sur la base de leur mesure de
la fonction de corrélation des groupes 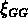 aux plus grandes échelles, ont
affirmé que le modèle de Kashlinsky expliquait leur résultat,
car selon eux il prévoit
une fonction de corrélation pour les petits groupes plus
faible que celle des galaxies.
aux plus grandes échelles, ont
affirmé que le modèle de Kashlinsky expliquait leur résultat,
car selon eux il prévoit
une fonction de corrélation pour les petits groupes plus
faible que celle des galaxies.
Mais je vais montrer que
le modèle de Kashlinsky, n'implique pas
une amplitude de la fonction de corrélation des
groupes
inférieure à celle des galaxies aux grandes échelles.
En fait, si nous voulons connaître la masse des systèmes
auxquels correspond une amplification donnée
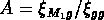 de la fonction de
corrélation croisée avec les galaxies, nous avons à partir des équations
(
de la fonction de
corrélation croisée avec les galaxies, nous avons à partir des équations
( ) et (
) et ( ):
):

tandis que pour l'amplification 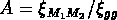 de la fonction de
corrélation de systèmes de masse m
relativement à la fonction de
corrélation des galaxies, nous avons à partir des équations
(
de la fonction de
corrélation de systèmes de masse m
relativement à la fonction de
corrélation des galaxies, nous avons à partir des équations
( ) et (
) et ( ):
):

Si l'on choisit n=-1 et  , alors
, alors 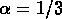 et
et
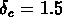 ,
et seuls les systèmes dont la masse est inférieure à
,
et seuls les systèmes dont la masse est inférieure à
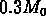 peuvent avoir une fonction de corrélation
d'amplitude inférieure à celle des galaxies
(toujours aux grandes échelles);
par exemple, pour avoir une amplitude qui soit la moitié de celle des
galaxies, il faut que
peuvent avoir une fonction de corrélation
d'amplitude inférieure à celle des galaxies
(toujours aux grandes échelles);
par exemple, pour avoir une amplitude qui soit la moitié de celle des
galaxies, il faut que 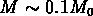 . Si, suivant Kashlinsky,
nous estimons
. Si, suivant Kashlinsky,
nous estimons
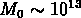 , c'est à dire la masse d'un groupe
avec 8-10 membres, il est clair qu'aucun système physique
ne peut satisfaire cette contrainte dans notre scénario!
Il est donc évident que mêmes les groupes pauvres doivent avoir
une fonction de corrélation comparable à celle des galaxies.
Si l'on avait pris
, c'est à dire la masse d'un groupe
avec 8-10 membres, il est clair qu'aucun système physique
ne peut satisfaire cette contrainte dans notre scénario!
Il est donc évident que mêmes les groupes pauvres doivent avoir
une fonction de corrélation comparable à celle des galaxies.
Si l'on avait pris 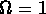 , on aurait eu un
, on aurait eu un
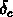 plus élevé et une contrainte encore plus stricte.
plus élevé et une contrainte encore plus stricte.
D'autre part, RGH90 dans une analyse de leur catalogue de 128
groupes sélectionnés à partir de la nouvelle tranche CfA de 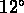 trouvent une fonction de corrélation entre groupes
comparable à celle des galaxies aux échelles
< 10
trouvent une fonction de corrélation entre groupes
comparable à celle des galaxies aux échelles
< 10 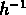 Mpc
(plus exactement, RGH89 ont défini un échantillon statistique
de 92 groupes, tandis que l'échantillon total est constitué de
128 groupes, la différence étant due au fait que l'échantillon
statistique de 92 groupes n'inclue pas les groupes qui se trouvent
proches des limites du catalogue; ci-après je suivrai
la numérotation de l'échantillon statistique, qui est faite
suivant les ascensions droites croîssantes).
Mpc
(plus exactement, RGH89 ont défini un échantillon statistique
de 92 groupes, tandis que l'échantillon total est constitué de
128 groupes, la différence étant due au fait que l'échantillon
statistique de 92 groupes n'inclue pas les groupes qui se trouvent
proches des limites du catalogue; ci-après je suivrai
la numérotation de l'échantillon statistique, qui est faite
suivant les ascensions droites croîssantes).




Next: Une analyse des
Up: Groupes de galaxies
Previous: Galaxies d'IRAS et
alberto cappi
Wed Feb 5 10:43:08 MET 1997
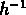 Mpc
(où les fluctuations ne sont pas linéaires) la fonction de corrélation
des amas devrait être égale à celle des galaxies;
en plus, les groupes comprenant plus de 8-10
membres (qui devraient représenter le système le plus commun
de la hiérarchie gravitationnelle actuelle, avec une masse
Mpc
(où les fluctuations ne sont pas linéaires) la fonction de corrélation
des amas devrait être égale à celle des galaxies;
en plus, les groupes comprenant plus de 8-10
membres (qui devraient représenter le système le plus commun
de la hiérarchie gravitationnelle actuelle, avec une masse
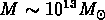 qui correspond à la masse de turnaround)
devraient avoir eux aussi une fonction de
corrélation identique à celle des galaxies.
Aux échelles dépassant celle de turnaround (
qui correspond à la masse de turnaround)
devraient avoir eux aussi une fonction de
corrélation identique à celle des galaxies.
Aux échelles dépassant celle de turnaround (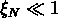 , où
, où
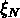 est la fonction d'autocorrélation de masse de la
distribution de masse primordiale), Kashlinsky arrive aux résultats suivants:
est la fonction d'autocorrélation de masse de la
distribution de masse primordiale), Kashlinsky arrive aux résultats suivants:

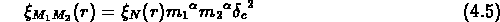

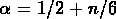 (voir le premier chapitre),
(voir le premier chapitre),
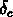 est le contraste de densité
critique
est le contraste de densité
critique 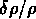 pour le turnaround,
et
pour le turnaround,
et 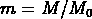 est le rapport entre la masse du système et la masse qui
correspond au turnaround.
La raison physique de la différence entre la relation
(
est le rapport entre la masse du système et la masse qui
correspond au turnaround.
La raison physique de la différence entre la relation
(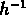 Mpc l'amplitude de la fonction
de corrélation angulaire et spatiale des groupes est
la moitié de celle des galaxies.
Mpc l'amplitude de la fonction
de corrélation angulaire et spatiale des groupes est
la moitié de celle des galaxies.
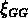 de leurs groupes a une amplitude 2.5
fois plus faible que celle des galaxies.
Il faut souligner que le résultats de Jing & Zhang et de Maia et da Costa
se refèrent à des échelles différentes.
En effet, Maia et da Costa observent justement que leur résultat
ne peut pas être comparé aux prévisions du modèle de
Kashlinsky, simplement parce qu'ils ne peuvent mesurer la
fonction de corrélation qu'aux échelles inférieures à
10
de leurs groupes a une amplitude 2.5
fois plus faible que celle des galaxies.
Il faut souligner que le résultats de Jing & Zhang et de Maia et da Costa
se refèrent à des échelles différentes.
En effet, Maia et da Costa observent justement que leur résultat
ne peut pas être comparé aux prévisions du modèle de
Kashlinsky, simplement parce qu'ils ne peuvent mesurer la
fonction de corrélation qu'aux échelles inférieures à
10 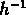 Mpc .
Mpc .
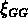 aux plus grandes échelles, ont
affirmé que le modèle de Kashlinsky expliquait leur résultat,
car selon eux il prévoit
une fonction de corrélation pour les petits groupes plus
faible que celle des galaxies.
aux plus grandes échelles, ont
affirmé que le modèle de Kashlinsky expliquait leur résultat,
car selon eux il prévoit
une fonction de corrélation pour les petits groupes plus
faible que celle des galaxies.
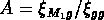 de la fonction de
corrélation croisée avec les galaxies, nous avons à partir des équations
(
de la fonction de
corrélation croisée avec les galaxies, nous avons à partir des équations
(
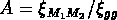 de la fonction de
corrélation de systèmes de masse m
relativement à la fonction de
corrélation des galaxies, nous avons à partir des équations
(
de la fonction de
corrélation de systèmes de masse m
relativement à la fonction de
corrélation des galaxies, nous avons à partir des équations
(
 , alors
, alors 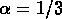 et
et
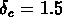 ,
et seuls les systèmes dont la masse est inférieure à
,
et seuls les systèmes dont la masse est inférieure à
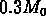 peuvent avoir une fonction de corrélation
d'amplitude inférieure à celle des galaxies
(toujours aux grandes échelles);
par exemple, pour avoir une amplitude qui soit la moitié de celle des
galaxies, il faut que
peuvent avoir une fonction de corrélation
d'amplitude inférieure à celle des galaxies
(toujours aux grandes échelles);
par exemple, pour avoir une amplitude qui soit la moitié de celle des
galaxies, il faut que 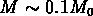 . Si, suivant Kashlinsky,
nous estimons
. Si, suivant Kashlinsky,
nous estimons
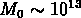 , c'est à dire la masse d'un groupe
avec 8-10 membres, il est clair qu'aucun système physique
ne peut satisfaire cette contrainte dans notre scénario!
Il est donc évident que mêmes les groupes pauvres doivent avoir
une fonction de corrélation comparable à celle des galaxies.
Si l'on avait pris
, c'est à dire la masse d'un groupe
avec 8-10 membres, il est clair qu'aucun système physique
ne peut satisfaire cette contrainte dans notre scénario!
Il est donc évident que mêmes les groupes pauvres doivent avoir
une fonction de corrélation comparable à celle des galaxies.
Si l'on avait pris 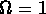 , on aurait eu un
, on aurait eu un
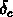 plus élevé et une contrainte encore plus stricte.
plus élevé et une contrainte encore plus stricte.
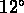 trouvent une fonction de corrélation entre groupes
comparable à celle des galaxies aux échelles
< 10
trouvent une fonction de corrélation entre groupes
comparable à celle des galaxies aux échelles
< 10 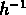 Mpc
(plus exactement, RGH89 ont défini un échantillon statistique
de 92 groupes, tandis que l'échantillon total est constitué de
128 groupes, la différence étant due au fait que l'échantillon
statistique de 92 groupes n'inclue pas les groupes qui se trouvent
proches des limites du catalogue; ci-après je suivrai
la numérotation de l'échantillon statistique, qui est faite
suivant les ascensions droites croîssantes).
Mpc
(plus exactement, RGH89 ont défini un échantillon statistique
de 92 groupes, tandis que l'échantillon total est constitué de
128 groupes, la différence étant due au fait que l'échantillon
statistique de 92 groupes n'inclue pas les groupes qui se trouvent
proches des limites du catalogue; ci-après je suivrai
la numérotation de l'échantillon statistique, qui est faite
suivant les ascensions droites croîssantes).