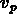 de la galaxie.
de la galaxie.
Avant de présenter le travail sur les amas, je vais résumer quelle est la situation pour les galaxies, et comment a été défini un ``plan fondamental" , ce qui permettra de mieux comprendre analogies et différences dans le cas des amas.
La connaissance du champ des vitesses est une information essentielle
si l'on veut accéder directement à la distribution de matière
dans l'Univers qui, comme on l'a déjà vu, peut différer de
la distribution de lumière. Mais il faut alors mesurer la distance vraie
d'une galaxie, pour séparer la composante de la vitesse radiale qui
est donnée par le flot de Hubble de la vitesse propre 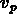 de la galaxie.
de la galaxie.

Une mesure de distance implique la mesure d'une quantité intrinsèque d'une galaxie, telle sa luminosité ou son rayon. Cela explique l'intérêt porté aux relations qui lient un paramètre mesurable à un paramètre intrinséque.
Par exemple, la relation de Tully-Fischer relie la magnitude absolue d'une galaxie dans une bande infrarouge à la largeur de la raie HI à 21 cm pour les galaxies spirales; pour les galaxies elliptiques, la relation de Faber-Jackson (1976) relie luminosité et dispersion de vitesse:

où la valeur de n est proche de 4.
On peut donc mesurer la distance d'une galaxie elliptique à partir de cette relation de manière indépendante du décalage vers le rouge. Le problème est que cette relation est assez bruitée, et ce fait a conduit à chercher si cette dispersion était corrélée à la variation d'un autre paramètre.
La nécessité d'un deuxième paramètre a été suggérée pour les galaxies spirales par Bujarrabal et al. (1981) et pour les galaxies elliptiques par Terlevich et al. (1981) et Tonry & Davis (1981).
Djorgovski & Davis (1987) ont trouvé pour les bulges et les galaxies elliptiques la relation suivante:
où 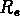 est le rayon de de Vaucouleurs,
est le rayon de de Vaucouleurs, 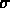 est la dispersion de
vitesse centrale, et
est la dispersion de
vitesse centrale, et 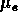 est la brillance de surface moyenne dans
le rayon
est la brillance de surface moyenne dans
le rayon 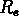 . Cette relation correspond à
. Cette relation correspond à

où L est la luminosité dans le rayon 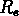 .
.
Parallèlement Dressler et al. (1987) trouvaient la relation:

où 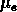 est la brillance de surface dans le rayon effectif
est la brillance de surface dans le rayon effectif
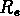 . Ils ont défini un nouveau paramètre,
. Ils ont défini un nouveau paramètre, 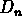 , le diamètre
de l'ouverture circulaire dans laquelle la brillance de surface
totale est
, le diamètre
de l'ouverture circulaire dans laquelle la brillance de surface
totale est  (comme valeur pratique ils ont choisi
(comme valeur pratique ils ont choisi
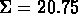 magnitudes bleues per arcsec
magnitudes bleues per arcsec ).
Ils ont alors établi une relation
).
Ils ont alors établi une relation 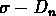 peu dispersée, qui
est en réalité une relation entre trois paramètres, car
peu dispersée, qui
est en réalité une relation entre trois paramètres, car 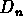 est une
combinaison de L et de
est une
combinaison de L et de 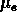 .
.
On peut se demander pour quelle raison les galaxies elliptiques suivent une telle relation à deux paramètres indépendants. Le théorème du viriel donne une justification très simple, interprétée par Djorgovski et al. (1988; voir aussi Djorgovski et Santiago, 1992) de la manière suivante.
Le théoreme du viriel implique:
où G est la constante de gravitation, M est la masse de la galaxie,
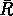 un rayon moyen défini de manière telle que l'expression à
gauche de l'équation (
un rayon moyen défini de manière telle que l'expression à
gauche de l'équation (![]() ) soit l'énergie potentielle,
et
) soit l'énergie potentielle,
et 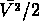 une énergie cinetique moyenne par unité de masse.
une énergie cinetique moyenne par unité de masse.
On peut définir pour une galaxie un rayon non-isophotale, par exemple le rayon de de Vaucouleurs:

où le facteur 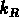 résume la structure de densité de la galaxie.
De manière analogue, on peut définir une vitesse V:
résume la structure de densité de la galaxie.
De manière analogue, on peut définir une vitesse V:

où le facteur 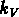 prend en considération la structure
cinématique de la galaxie (anisotropies, etc.);
et une brillance de surface moyenne
prend en considération la structure
cinématique de la galaxie (anisotropies, etc.);
et une brillance de surface moyenne 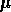 :
:

où 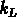 reflète la structure en luminosité de la galaxie,
qui dépend de la région spectrale choisie.
reflète la structure en luminosité de la galaxie,
qui dépend de la région spectrale choisie.
De l'équation (![]() ) nous avons alors:
) nous avons alors:

où le paramètre de structure K est:

ou alternativement:

ce qui définit un plan dans l'espace à trois dimensions 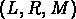 ,
dit ``plan fondamental" .
,
dit ``plan fondamental" .
Djorgovski et Santiago (1992) remarquent que K et 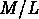 dépendent de l'histoire de la formation et de l'évolution des galaxies
elliptiques. La remarquable ``minceur" du
plan fondamental ,
implique un homogénéité significative des galaxies elliptiques,
avec des facteurs
dépendent de l'histoire de la formation et de l'évolution des galaxies
elliptiques. La remarquable ``minceur" du
plan fondamental ,
implique un homogénéité significative des galaxies elliptiques,
avec des facteurs 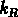 ,
, 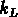 et
et 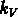 presque constants.
De cette hypothèse d'homogéneité, Faber et al. (1987) et
Djorgovski (1988) ont déduit la relation suivante:
presque constants.
De cette hypothèse d'homogéneité, Faber et al. (1987) et
Djorgovski (1988) ont déduit la relation suivante:

où 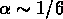 .
.
Il y a tout un ensemble des structures (formées d'étoiles)
pour lesquelles on a déjà trouvé ou suggéré des relations de type
Faber-Jackson ou même ``plan fondamental".
Meylan et Major (1986) et, successivement,
Paturel et Garnier (1992) ont observé que
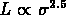 pour les amas globulaires,
et Held et al. trouvent
pour les amas globulaires,
et Held et al. trouvent 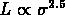 pour les
galaxies naines. Nieto et al. (1990) ont suggéré que
les galaxies elliptiques de petite masse,
les amas globulaires
et les galaxies spheroidales naines
se trouvent aussi sur un plan
fondamental proche de celui défini par les galaxies elliptiques
(mais de Carvalho & Djorgovski, 1992, trouvent que les galaxies
spheroidales naines forment une famille à un paramètre).
pour les
galaxies naines. Nieto et al. (1990) ont suggéré que
les galaxies elliptiques de petite masse,
les amas globulaires
et les galaxies spheroidales naines
se trouvent aussi sur un plan
fondamental proche de celui défini par les galaxies elliptiques
(mais de Carvalho & Djorgovski, 1992, trouvent que les galaxies
spheroidales naines forment une famille à un paramètre).
Le plan fondamental comme je l'ai présenté est une combinaison
de quantités observables, telle la brillance de surface,
le rayon, la dispersion de vitesse.
Or, Bender et al. (1992) ont voulu choisir des
paramètres qui sont directement liée à des quantités physiques;
ainsi ils sont défini trois autres variables, 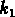 ,
,
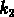 et
et 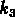 :
:
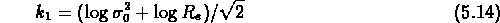
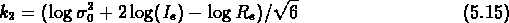
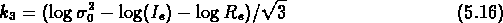
où 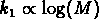 ,
, 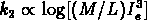 et
et
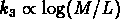 .
.
La projection 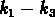 représente alors
le plan fondamental
vu pratiquement de profil, et la projection
représente alors
le plan fondamental
vu pratiquement de profil, et la projection 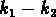 montre
le plan fondamental vu pratiquement de face.
Pourtant il faut remarquer que la relation
montre
le plan fondamental vu pratiquement de face.
Pourtant il faut remarquer que la relation 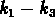 n'est pas le plan
fondamental: elle le serait seulement si
n'est pas le plan
fondamental: elle le serait seulement si 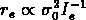 .
.