



Next: Explication d'une fausse
Up: Les fonctions de
Previous: La question de
Deux groupes ont cherché à réduire ces effets de projection
en sélectionnant les amas avec un algorithme de recherche automatique.
Dans l' Edinburgh-Durham Southern Galaxy Catalogue,
l'algorithme applique une correction pour séparer les amas
superposés, et les galaxies dans la région de superposition
sont attribuées à un amas ou à l'autre grâce à
un ajustement gaussien du profil de densité de chaque amas
(Nichol et al., 1992).
Le rayon de recherche r est fixé à 1 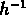 Mpc , pour
réduire les projections. Ils calculent ensuite
Mpc , pour
réduire les projections. Ils calculent ensuite 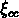 pour un sous-échantillon de 89 amas (dont 79 avec un décalage
vers le rouge mesuré) défini selon les critères suivants:
pour un sous-échantillon de 89 amas (dont 79 avec un décalage
vers le rouge mesuré) défini selon les critères suivants:
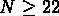 , où N est le nombre de galaxies dans le cercle de rayon r et
de magnitude m telle que
, où N est le nombre de galaxies dans le cercle de rayon r et
de magnitude m telle que 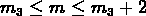 ,
, 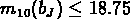 ,
et
,
et 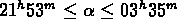 et
et
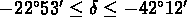 . Nichol et al. (1992) trouvent
. Nichol et al. (1992) trouvent
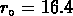 et
et 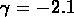 .
.
Dans le catalogue APM, l'algorithme identifie les régions qui ont
la plus grande densité de galaxies de magnitude 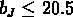 ; ces
régions sont identifiées grâce à une technique de percolation,
avec un rayon de recherche égal à 0.7 fois la séparation moyenne.
Chaque groupe recensant plus de 20 galaxies est ensuite choisi comme candidat.
Le rayon utilisé pour compter les amas est de
; ces
régions sont identifiées grâce à une technique de percolation,
avec un rayon de recherche égal à 0.7 fois la séparation moyenne.
Chaque groupe recensant plus de 20 galaxies est ensuite choisi comme candidat.
Le rayon utilisé pour compter les amas est de 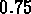
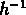 Mpc .
Les auteurs calculent
Mpc .
Les auteurs calculent
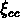 pour 190 amas et trouvent
pour 190 amas et trouvent 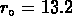
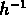 Mpc
et
Mpc
et 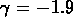 (Dalton et al., 1992).
(Dalton et al., 1992).
Les 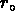 trouvés pour ces amas sélectionnés automatiquement
sont inférieurs à la longueur de corrélation
trouvés pour ces amas sélectionnés automatiquement
sont inférieurs à la longueur de corrélation 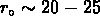
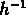 Mpc
déterminée à partir des différents échantillons d'amas d'Abell ou ACO.
Mpc
déterminée à partir des différents échantillons d'amas d'Abell ou ACO.
La situation se complique, car l'amplitude de la corrélation
semblerait plus forte pour les
amas plus riches. L'existence d'une relation bien définie, et cela
jusqu'aux échelles des superamas, comme le soutiennent par exemple
Bahcall et West (1992), n'est pas définitivement prouvée.
Les échantillons d'amas de richesse 1 ou plus sont très petits
(pour ne pas parler des superamas),
et d'autres analyses, comme par exemple celle de
Postman, Huchra & Geller (1992), ou la nôtre (Cappi & Maurogordato, 1992),
ne trouvent pas de différence notable entre la corrélation des amas de
richesse 0 et celle des autres amas.
Mais il est vrai que les groupes pauvres, comme j'ai eu
l'occasion de le montrer, ont une corrélation comparable à celle
des galaxies; les amas riches, même quand on considère
les effets de projection, ont une amplitude supérieure à celle des
galaxies. Ce qui est intéressant est que les ``amas" detectés dans
les deux catalogues automatiques sont en effet des groupes riches
ou des amas de richesse 0 selon la classification d'Abell .
Il y a donc là une indéniable variation de l'amplitude en
fonction de la richesse (ou aussi en fonction de la densité
moyenne des objets considerés, puisque les objets les plus riches sont
aussi les plus rares).
Si cela est vrai, alors le fait que l'amplitude
de la fonction de corrélation des
amas
dans les catalogues automatiques
soit plus petite que celle des amas d'Abell ne représente
pas en soi une contradiction.
J'ajouterai que les catalogues automatiques n'ont pas beaucoup d'objets,
donc l'incertitude des résultats statistique est relativement grande.
Il faut aussi ajouter que le fait qu'un catalogue d'amas soit ``automatique",
n'implique pas l' ``objectivité" ou l'absence d'effets de sélection
(après tout, il s'agit toujours d'une recherche sur des images
bidimensionnelles).
Et sous ce jour, les catalogues automatiques sont trop récents et trop
peu étudiés pour qu'on puisse être sûrs de leur fiabilité.
Ceci dit, il est évident que dans le futur la sélection des objets par
des algorithmes de plus en plus perfectionnés sera la seule voie praticable.




Next: Explication d'une fausse
Up: Les fonctions de
Previous: La question de
alberto cappi
Wed Feb 5 10:43:08 MET 1997
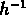 Mpc , pour
réduire les projections. Ils calculent ensuite
Mpc , pour
réduire les projections. Ils calculent ensuite 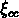 pour un sous-échantillon de 89 amas (dont 79 avec un décalage
vers le rouge mesuré) défini selon les critères suivants:
pour un sous-échantillon de 89 amas (dont 79 avec un décalage
vers le rouge mesuré) défini selon les critères suivants:
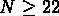 , où N est le nombre de galaxies dans le cercle de rayon r et
de magnitude m telle que
, où N est le nombre de galaxies dans le cercle de rayon r et
de magnitude m telle que 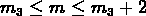 ,
, 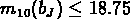 ,
et
,
et 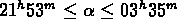 et
et
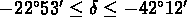 . Nichol et al. (1992) trouvent
. Nichol et al. (1992) trouvent
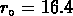 et
et 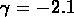 .
.
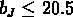 ; ces
régions sont identifiées grâce à une technique de percolation,
avec un rayon de recherche égal à 0.7 fois la séparation moyenne.
Chaque groupe recensant plus de 20 galaxies est ensuite choisi comme candidat.
Le rayon utilisé pour compter les amas est de
; ces
régions sont identifiées grâce à une technique de percolation,
avec un rayon de recherche égal à 0.7 fois la séparation moyenne.
Chaque groupe recensant plus de 20 galaxies est ensuite choisi comme candidat.
Le rayon utilisé pour compter les amas est de 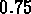
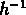 Mpc .
Les auteurs calculent
Mpc .
Les auteurs calculent
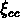 pour 190 amas et trouvent
pour 190 amas et trouvent 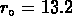
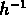 Mpc
et
Mpc
et 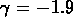 (Dalton et al., 1992).
(Dalton et al., 1992).
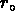 trouvés pour ces amas sélectionnés automatiquement
sont inférieurs à la longueur de corrélation
trouvés pour ces amas sélectionnés automatiquement
sont inférieurs à la longueur de corrélation 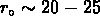
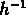 Mpc
déterminée à partir des différents échantillons d'amas d'Abell
Mpc
déterminée à partir des différents échantillons d'amas d'Abell