



Next: La fonction de
Up: Les fonctions de
Previous: La sélection automatique
Postman et al. (1991) ont étudié
un échantillon de 208 amas dans l'hémisphère nord
limité à 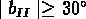 ,
, 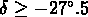 ,
,
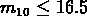 , et
, et 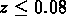 . Cet échantillon (NST) contient 208 amas.
Ils l'ont défini comme étant ``statistique", car le choix des limites
devrait
minimiser les effets de sélection .
Pour cet échantillon, Postman et al. trouvent
. Cet échantillon (NST) contient 208 amas.
Ils l'ont défini comme étant ``statistique", car le choix des limites
devrait
minimiser les effets de sélection .
Pour cet échantillon, Postman et al. trouvent
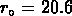
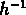 Mpc ; cependant, dans un autre article,
Efstathiou et al. (1992) analysent le même échantillon, et
trouvent
Mpc ; cependant, dans un autre article,
Efstathiou et al. (1992) analysent le même échantillon, et
trouvent 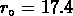 . Ils affirment d'avoir utilisé
pratiquement la même méthode de Postman et al. pour
mesurer
. Ils affirment d'avoir utilisé
pratiquement la même méthode de Postman et al. pour
mesurer 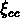 , et ne peuvent pas expliquer la raison
de cette différence.
, et ne peuvent pas expliquer la raison
de cette différence.
J'ai réanalysé le même échantillon, en collaboration avec S. Maurogordato.
Les distances comobiles ont été calculées à partir des décalages
vers le rouge:
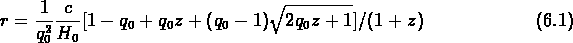
avec 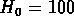 km/s/Mpc et
km/s/Mpc et 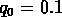 (comme Postman et al.).
(comme Postman et al.).
Les catalogues aléatoires de normalisation ont été
construits à partir de la même distribution observée en décalage
vers le rouge
(en pratique, on a pris les décalages vers le rouge des amas observés et
on les a attribué aux points aléatoires suivant une probabilité
gaussienne avec 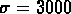 km/s, pour tenir compte d'une
certaine sélection, surtout entre
km/s, pour tenir compte d'une
certaine sélection, surtout entre  ).
On a aussi apporté des corrections en fonction de la latitude galactique
(la probabilité de détection d'un amas varie avec sa distance au plan
galactique) et de la déclinaison (un effet qui est probablement dû
à la variation de la probabilité de détection d'un amas avec sa
distance zénithale). Dans l'analyse de nos échantillons,
ces deux corrections ne sont pas importantes.
).
On a aussi apporté des corrections en fonction de la latitude galactique
(la probabilité de détection d'un amas varie avec sa distance au plan
galactique) et de la déclinaison (un effet qui est probablement dû
à la variation de la probabilité de détection d'un amas avec sa
distance zénithale). Dans l'analyse de nos échantillons,
ces deux corrections ne sont pas importantes.
La fig. montre une
comparaison entre corrélations calculées de manière différente.
montre une
comparaison entre corrélations calculées de manière différente.

Figure: 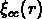 pour l'échantillon NST.
pour l'échantillon NST.
Nous avons trouvé que la différence en 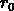 peut très simplement être
expliquée par la différence en pas utilisé pour l'estimation de
peut très simplement être
expliquée par la différence en pas utilisé pour l'estimation de
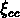 .
Avec un pas logarithmique de
.
Avec un pas logarithmique de 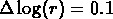 nous trouvons
nous trouvons
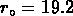
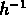 Mpc . Cette valeur est inférieure à celle de Postman et al.
parce que nous avons seulement consideré pour l'ajustement les points entre
3 et 45
Mpc . Cette valeur est inférieure à celle de Postman et al.
parce que nous avons seulement consideré pour l'ajustement les points entre
3 et 45 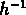 Mpc , où
Mpc , où 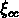 est toujours positive.
Cette valeur est supérieure à celle
d'Efstathiou et al. simplement parce que ces auteurs ont utilisé un pas
logarithmique de 0.2. Cela revient à ne pas estimer
est toujours positive.
Cette valeur est supérieure à celle
d'Efstathiou et al. simplement parce que ces auteurs ont utilisé un pas
logarithmique de 0.2. Cela revient à ne pas estimer
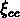 avec un résolution suffisante pour pouvoir détecter
du signal autour de 45
avec un résolution suffisante pour pouvoir détecter
du signal autour de 45 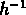 Mpc , et c'est pour cela que Efstathiou et al.
trouvent une corrélation toujours positive jusqu' à 30
Mpc , et c'est pour cela que Efstathiou et al.
trouvent une corrélation toujours positive jusqu' à 30 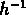 Mpc .
Mpc .




Next: La fonction de
Up: Les fonctions de
Previous: La sélection automatique
alberto cappi
Wed Feb 5 10:43:08 MET 1997
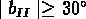 ,
, 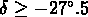 ,
,
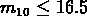 , et
, et 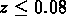 . Cet échantillon (NST) contient 208 amas.
Ils l'ont défini comme étant ``statistique", car le choix des limites
devrait
minimiser les effets de sélection .
Pour cet échantillon, Postman et al. trouvent
. Cet échantillon (NST) contient 208 amas.
Ils l'ont défini comme étant ``statistique", car le choix des limites
devrait
minimiser les effets de sélection .
Pour cet échantillon, Postman et al. trouvent
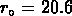
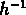 Mpc ; cependant, dans un autre article,
Efstathiou et al. (1992) analysent le même échantillon, et
trouvent
Mpc ; cependant, dans un autre article,
Efstathiou et al. (1992) analysent le même échantillon, et
trouvent 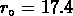 . Ils affirment d'avoir utilisé
pratiquement la même méthode de Postman et al. pour
mesurer
. Ils affirment d'avoir utilisé
pratiquement la même méthode de Postman et al. pour
mesurer 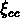 , et ne peuvent pas expliquer la raison
de cette différence.
, et ne peuvent pas expliquer la raison
de cette différence.
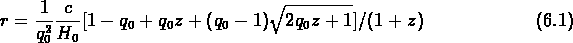
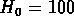 km/s/Mpc et
km/s/Mpc et 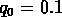 (comme Postman et al.).
(comme Postman et al.).
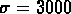 km/s, pour tenir compte d'une
certaine sélection, surtout entre
km/s, pour tenir compte d'une
certaine sélection, surtout entre  ).
On a aussi apporté des corrections en fonction de la latitude galactique
(la probabilité de détection d'un amas varie avec sa distance au plan
galactique) et de la déclinaison (un effet qui est probablement dû
à la variation de la probabilité de détection d'un amas avec sa
distance zénithale). Dans l'analyse de nos échantillons,
ces deux corrections ne sont pas importantes.
).
On a aussi apporté des corrections en fonction de la latitude galactique
(la probabilité de détection d'un amas varie avec sa distance au plan
galactique) et de la déclinaison (un effet qui est probablement dû
à la variation de la probabilité de détection d'un amas avec sa
distance zénithale). Dans l'analyse de nos échantillons,
ces deux corrections ne sont pas importantes.

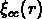 pour l'échantillon NST.
pour l'échantillon NST.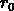 peut très simplement être
expliquée par la différence en pas utilisé pour l'estimation de
peut très simplement être
expliquée par la différence en pas utilisé pour l'estimation de
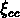 .
Avec un pas logarithmique de
.
Avec un pas logarithmique de 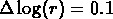 nous trouvons
nous trouvons
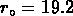
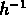 Mpc . Cette valeur est inférieure à celle de Postman et al.
parce que nous avons seulement consideré pour l'ajustement les points entre
3 et 45
Mpc . Cette valeur est inférieure à celle de Postman et al.
parce que nous avons seulement consideré pour l'ajustement les points entre
3 et 45 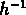 Mpc , où
Mpc , où 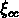 est toujours positive.
Cette valeur est supérieure à celle
d'Efstathiou et al. simplement parce que ces auteurs ont utilisé un pas
logarithmique de 0.2. Cela revient à ne pas estimer
est toujours positive.
Cette valeur est supérieure à celle
d'Efstathiou et al. simplement parce que ces auteurs ont utilisé un pas
logarithmique de 0.2. Cela revient à ne pas estimer
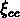 avec un résolution suffisante pour pouvoir détecter
du signal autour de 45
avec un résolution suffisante pour pouvoir détecter
du signal autour de 45 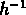 Mpc , et c'est pour cela que Efstathiou et al.
trouvent une corrélation toujours positive jusqu' à 30
Mpc , et c'est pour cela que Efstathiou et al.
trouvent une corrélation toujours positive jusqu' à 30 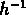 Mpc .
Mpc .