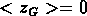 , et
, et
La composante cosmologique du décalage vers le rouge d'un amas n'est pas un paramètre observable directement, car nous pouvons seulement accéder aux décalages vers le rouge des galaxies individuelles. Il faut donc adopter une procédure qui puisse nous donner cette quantité, avec en outre la dispersion de vitesse de l'amas et les erreurs associées, et qui effectue toutes les corrections nécessaires. Dans ce qui suit, je décrirai la procédure de Danese et al. (1980), que j'ai utilisée pour étudier quelques amas du catalogue ACO.
Supposons connaître un nombre n de décalages vers le rouge de galaxies dans le champ d'un amas.
Nous ferons l'hypothèse que le redshift d'une galaxie est indépendant
de sa masse.
Alors 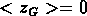 , et
, et
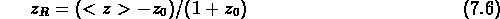
Cela est vrai si l'amas dans lequel la galaxie se trouve a subi une relaxation violente (Lynden-Bell, 1967), avec équipartition des vitesses, et qu'il se trouve encore dans la phase initiale de relaxation à deux corps, qui cause l'equipartition de l'énergie.
Pour calculer le décalage vers le rouge moyen observé de l'amas,
il faut calculer la moyenne des
n décalages vers le rouge observés 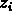 des galaxies, et il
est naturellement indispensable d'avoir une estimation fiable
des erreurs qui affectent cette mesure.
des galaxies, et il
est naturellement indispensable d'avoir une estimation fiable
des erreurs qui affectent cette mesure.
Or, nous sommes confrontés à deux types d'erreurs:
les erreurs dûes à l'incertitude sur chaque 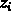 ,
(qui dérivent de la résolution finie de l'instrument, des
calibrations, etc.), et les sampling errors, dues au nombre fini
d'objets utilisés pour estimer la vraie distribution.
,
(qui dérivent de la résolution finie de l'instrument, des
calibrations, etc.), et les sampling errors, dues au nombre fini
d'objets utilisés pour estimer la vraie distribution.
La première incertitude due aux erreurs d'observation
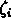 (i=1,...n est simplement donnée
par
(i=1,...n est simplement donnée
par 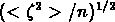 .
L'estimation des sampling errors n'est pas difficile
si l'on fait comme autre hypothèse que les décalages vers le rouge
suivent une distribution normale. Cela semble être souvent le cas
(Yahil et Vidal, 1977), et cette hypothèse a des
justifications theoriques. Il ne faut pas oublier pour autant les
cas de sous-structures existant dans des amas subclustering.
Si
.
L'estimation des sampling errors n'est pas difficile
si l'on fait comme autre hypothèse que les décalages vers le rouge
suivent une distribution normale. Cela semble être souvent le cas
(Yahil et Vidal, 1977), et cette hypothèse a des
justifications theoriques. Il ne faut pas oublier pour autant les
cas de sous-structures existant dans des amas subclustering.
Si 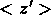 et
et 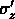 sont les estimations, calculées à
partir d'un échantillon avec n galaxies, respectivement du vrai
décalage vers le rouge moyen et du vrai écart-type,
alors dans ce cas la quantité
sont les estimations, calculées à
partir d'un échantillon avec n galaxies, respectivement du vrai
décalage vers le rouge moyen et du vrai écart-type,
alors dans ce cas la quantité
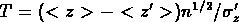 suit la distribution de
Student t avec
suit la distribution de
Student t avec 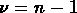 degrés de liberté.
degrés de liberté.
Il est convenient de choisir une incertitude au niveau de confiance
de 68%, car la t(0.68) de Student devient 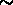 1
pour
1
pour 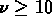 .
.
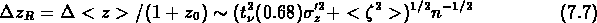
où 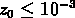 a été negligé.
a été negligé.
Nous pouvons calculer la vitesse radiale 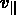 de chaque galaxie
relative à la vitesse moyenne observée de l'amas (que nous avons supposée
coïncider avec le centre de masse de l'amas):
de chaque galaxie
relative à la vitesse moyenne observée de l'amas (que nous avons supposée
coïncider avec le centre de masse de l'amas):
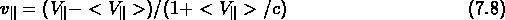
Pour estimer la dispersion de vitesse 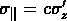 ,
nous devons soustraire la contribution donnée par les erreurs de mesure des
vitesses
,
nous devons soustraire la contribution donnée par les erreurs de mesure des
vitesses 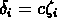 :
:
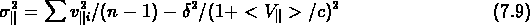
Avec les hypothèses que nous avons exposées, si  est la
vraie dispersion de vitesse de l'amas, alors
la quantité
est la
vraie dispersion de vitesse de l'amas, alors
la quantité 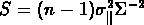 suit
une distribution du
suit
une distribution du 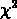 .
.
Les incertitudes 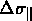 dans la dispersion de vitesse,
avec par exemple un niveau de confiance de 68%, peuvent ainsi être
estimées:
dans la dispersion de vitesse,
avec par exemple un niveau de confiance de 68%, peuvent ainsi être
estimées:
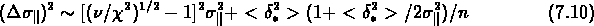
où 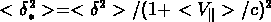 .
.
Finalement, si nous voulons avoir des quantités physiques telles ques les distances, ou les temps de regard en arrière ( lookback times), à partir des décalages vers le rouge cosmologiques, il nous reste à choisir un modèle cosmologique.
Beers et al. (1990) ont décrit d'autres statistiques ``robustes" qui ne dépendent pas de l'hypothèse de gaussianité des vitesses de l'amas; ils notent qu'en présence d'écarts aux conditions gaussiennes, la méthode de Danese et al. peut conduire à des intervalles de confiance trop grands pour l'estimation de la moyenne et des intervalles trop petits pour la dispersion. Or, il est vrai que l'existence éventuelle de sous-structures et le petit nombre d'objets pris en considération peut conduire à des erreurs, qui affectent significativement la détermination de la masse de l'amas, car elle dépend du carré de la dispersion de vitesse. Néanmoins, l'expérience montre que lorsque l'on étudie des amas réguliers, les résultats obtenus avec les diverses statistiques ne sont pas significativement différents.
Je fais ici une dernière considération à propos de la mesure
de la dispersion de vitesse d'un amas. Les observations nous donnent un
échantillon de galaxies à z différents. Si le décalage vers
le rouge d'une galaxie est très différent du redshift moyen des
autres galaxies, il est évident
que la galaxie ne fait pas partie de l'amas. Si, au contraire,
la différence est légère, il y a un certain degré d'ambiguïté
sur l'appartenance ou non de la galaxie à l'amas.
Un critère qui permet de discriminer les
membres d'un amas est la
méthode du 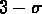 clipping (Yahil & Vidal, 1977).
Il faut calculer le z moyen des galaxies; on sélectionne le z qui
s'écarte le plus de cette valeur moyenne, et l'on
recalcule le z moyen sans tenir compte de cet objet. Si le décalage vers
le rouge de
l'objet est à plus de
clipping (Yahil & Vidal, 1977).
Il faut calculer le z moyen des galaxies; on sélectionne le z qui
s'écarte le plus de cette valeur moyenne, et l'on
recalcule le z moyen sans tenir compte de cet objet. Si le décalage vers
le rouge de
l'objet est à plus de 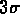 de la nouvelle moyenne, alors on
considère qu'il n'est pas membre de l'amas, et on recommence avec
la même procédure, jusqu'au moment où le décalage vers le
rouge qui s'écarte le plus de la moyenne est néanmoins à moins
de
de la nouvelle moyenne, alors on
considère qu'il n'est pas membre de l'amas, et on recommence avec
la même procédure, jusqu'au moment où le décalage vers le
rouge qui s'écarte le plus de la moyenne est néanmoins à moins
de 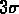 de la moyenne des autres décalages vers le rouge.
de la moyenne des autres décalages vers le rouge.