Dans cette thèse, j'ai plusieurs fois parlé de décalage vers le rouge, ou redshift, qui reste notre outil principal pour accéder aux vitesses et aux distances des galaxies aux échelles cosmologiques.
Une discussion sur l'interprétation correcte du décalage vers le rouge dans les amas des galaxies est donnée par Harrison (1974).
Le décalage vers le rouge d'une galaxie est défini par (voir
le premier chapitre, equation ![]() ):
):

Mais différentes composantes contribuent au redshift observé d'une galaxie dans un amas.
C'est le produit de ces composantes qui donne le décalage vers le rouge z mesuré par l'observateur:
Les contributions dans (![]() ) et (
) et (![]() ) représent
des effets Doppler relativistes, où
) représent
des effets Doppler relativistes, où 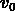 est notre vitesse propre
et
est notre vitesse propre
et 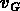 est la vitesse propre de la galaxie observée.
Nous devons soustraire la contribution
est la vitesse propre de la galaxie observée.
Nous devons soustraire la contribution
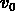 due à notre mouvement propre, qui devrait être
mesuré par rapport au référentiel du rayonnement cosmique de fond
(mais on corrige en général simplement du
mouvement du soleil autour du centre de notre galaxie).
En plus, on doit tenir compte du mouvement propre
de la galaxie observée par rapport à sa position comobile R.
due à notre mouvement propre, qui devrait être
mesuré par rapport au référentiel du rayonnement cosmique de fond
(mais on corrige en général simplement du
mouvement du soleil autour du centre de notre galaxie).
En plus, on doit tenir compte du mouvement propre
de la galaxie observée par rapport à sa position comobile R.
Dans le cas d'un amas, il serait plus approprié de prendre en compte
un quatrième terme, 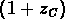 , qui correspond à la
vitesse propre
, qui correspond à la
vitesse propre 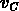 du centre de masse de l'amas relativement
à la position comobile R; ici
du centre de masse de l'amas relativement
à la position comobile R; ici 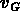 devrait être mesurée
par rapport au centre de masse de l'amas, avec l'avantage que
devrait être mesurée
par rapport au centre de masse de l'amas, avec l'avantage que
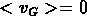 .
.
Etant donné que 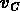 est en général inconnu, ou
difficile à déterminer, on suppose que l'observateur comobile en
R se déplace avec le centre de masse de l'amas et l'on suppose
vraie la condition
est en général inconnu, ou
difficile à déterminer, on suppose que l'observateur comobile en
R se déplace avec le centre de masse de l'amas et l'on suppose
vraie la condition 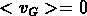 .
.
La contribution cosmologique dans l'équation (![]() ) est due à
l'expansion de l'Univers, et elle n'est pas proprement un effet Doppler.
) est due à
l'expansion de l'Univers, et elle n'est pas proprement un effet Doppler.