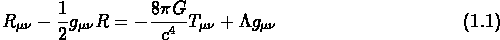
La Relativité Générale a fourni un cadre physique cohérent et élégant à la description de l'Univers: elle est la théorie sur laquelle se basent les modèles cosmologiques dans lesquels on interprète les observations. Je décrirai brièvement les caractéristiques de ces modèles, et je donnerai les définitions de quelques quantités fondamentales qui seront utilisées (ou auxquelles je ferai référence) dans la suite.
Les équations d'Einstein peuvent être écrites:
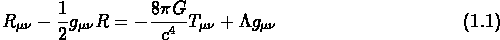
où 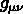 est la métrique de l'Univers,
est la métrique de l'Univers, 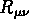 est le
tenseur de Ricci,
est le
tenseur de Ricci, 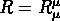 est la courbure,
est la courbure, 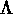 est la
constante cosmologique, G est la constante de
gravitation universelle et
est la
constante cosmologique, G est la constante de
gravitation universelle et 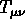 est le tenseur énergie-impulsion.
Si l'on considère un univers homogène et isotrope
( Principe Cosmologique) sa métrique sera celle de
Robertson -- Walker:
est le tenseur énergie-impulsion.
Si l'on considère un univers homogène et isotrope
( Principe Cosmologique) sa métrique sera celle de
Robertson -- Walker:
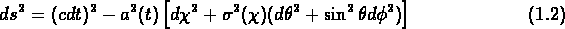
où 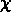 ,
, 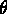 et
et 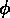 sont coordonnés comobiles,
t est le temps propre,
sont coordonnés comobiles,
t est le temps propre, 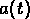 est le facteur d'échelle, c est
la vitesse de la lumière.
est le facteur d'échelle, c est
la vitesse de la lumière.
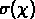 est une fonction dont la forme dépend du
paramètre de courbure K, qui peut avoir seulement les trois
valeurs -1, 0, +1:
est une fonction dont la forme dépend du
paramètre de courbure K, qui peut avoir seulement les trois
valeurs -1, 0, +1:
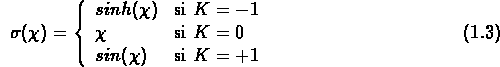
Si l'on suppose que la constante cosmologique 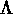 est nulle,
on trouve les équations de Friedman:
est nulle,
on trouve les équations de Friedman:
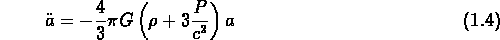

où 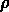 est la densité d'énergie et P la pression;
les deux équations sont liées par la loi d'expansion adiabatique de
l'Univers:
est la densité d'énergie et P la pression;
les deux équations sont liées par la loi d'expansion adiabatique de
l'Univers:

On peut définir la densité critique:

où H est la constante de Hubble,

et le paramètre  , normalisant la densité de l'Univers à la
densité critique:
, normalisant la densité de l'Univers à la
densité critique:

Il est évident que H est constante dans l'espace, mais dépend du temps,
comme  :
c'est pour ça qu'on utilise les notations
:
c'est pour ça qu'on utilise les notations 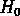 et
et 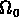 quand ces quantités sont mesurées au temps actuel.
Puisque
quand ces quantités sont mesurées au temps actuel.
Puisque 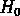 est connu avec une incertitude d'un facteur
est connu avec une incertitude d'un facteur 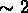 (
(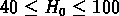 km sec
km sec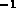 Mpc
Mpc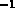 )
j'utiliserai dans la suite la notation pratique
)
j'utiliserai dans la suite la notation pratique 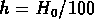 .
.
D'un point de vue observationnel, l'expansion de l'Univers provoque une augmentation de la longueur d'onde du rayonnement. On définit
où 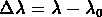 est la différence entre
la longueur d'onde observée
est la différence entre
la longueur d'onde observée 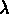 et
la longueur d'onde ``à repos", ou longueur d'onde propre,
et
la longueur d'onde ``à repos", ou longueur d'onde propre,
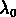 (telle qu'elle serait mesurée
par un observateur à la source).
Alors le décalage vers le rouge ( redshift) dû à l'expansion de
l'Univers est:
(telle qu'elle serait mesurée
par un observateur à la source).
Alors le décalage vers le rouge ( redshift) dû à l'expansion de
l'Univers est:

c'est à dire que 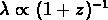 .
.
La géométrie de l'Univers dépend de K, qui détermine le
signe de 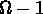 :
si K=1,
:
si K=1,  , et l'Univers est fermé, si K=-1,
, et l'Univers est fermé, si K=-1,
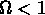 et l'Univers est ouvert; si K = 0, l'Univers est plat.
Les modèles de Friedman--Lemaître sont caractérisés par
la valeur de
et l'Univers est ouvert; si K = 0, l'Univers est plat.
Les modèles de Friedman--Lemaître sont caractérisés par
la valeur de  et par l'équation d'état
et par l'équation d'état

où 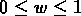 .
Il y a trois cas extrêmes qui sont aussi les plus intéressants:
si
.
Il y a trois cas extrêmes qui sont aussi les plus intéressants:
si 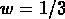 on a un univers de pur rayonnement, où
on a un univers de pur rayonnement, où
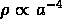 ; si w = 0 on a un univers de pure
matière, où
; si w = 0 on a un univers de pure
matière, où 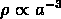 ; si w = -1 on a un
Univers dominé par l'énergie du vide, où
; si w = -1 on a un
Univers dominé par l'énergie du vide, où 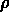 est
constante.
Il faut noter que les formules analytiques derivées dans le cadre
de ces modèles, et qui donnent des grandeurs physiques en
fonction du redshift, utilisent le paramètre d'accéleration
est
constante.
Il faut noter que les formules analytiques derivées dans le cadre
de ces modèles, et qui donnent des grandeurs physiques en
fonction du redshift, utilisent le paramètre d'accéleration
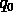 :
:

Donc dans le cas d'un univers dominé par la matière
(qui correspond à l'Univers actuel) 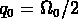 .
Un autre quantité importante est l'âge de l'Univers à un redshift
z. La formule la plus simple correspond à
.
Un autre quantité importante est l'âge de l'Univers à un redshift
z. La formule la plus simple correspond à 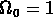 et
w = 0:
et
w = 0:

(voir table en appendice).
Si K = 0, 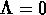 et P = 0,
et P = 0, 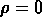 , (Univers vide)
on a une solution intéressante des équations d'Einstein, le modèle
de de Sitter (1917), qui donne une expansion exponentielle.
, (Univers vide)
on a une solution intéressante des équations d'Einstein, le modèle
de de Sitter (1917), qui donne une expansion exponentielle.
Dans l'interprétation moderne, la constante cosmologique est liée à l'énergie du vide. Le terme cosmologique correspond à

et

L'equation d'état pour l'énergie du vide est donnée alors par
La solution de de Sitter donne

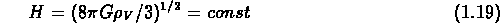

On verra que l'Univers est probablement passé par une phase d'expansion exponentielle.