



Next: Matière noire et
Up: Structures à grande
Previous: Les modèles de
Une fois défini un modèle cosmologique, nous somes confrontés
au problème de
comprendre la formation et l'évolution des structures dans l'Univers.
Dans une première phase après le Big Bang,
des fluctuations de densité (dont l'origine sera
discutée ensuite) ont crû linéairement sous
l'action de la gravitation; après la recombinaison, les photons ont
conservé le niveau des fluctuations (et le fond
diffus nous dit que à 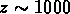 les fluctuations
à toutes les échelles étaient plus petites de
les fluctuations
à toutes les échelles étaient plus petites de 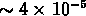 ), tandis que les fluctuations
de densité ont continué leur croissance; c'est dans cette phase, où
à certaines échelles les fluctuations deviennent non-linéaires,
que se forment les objets lumineux.
), tandis que les fluctuations
de densité ont continué leur croissance; c'est dans cette phase, où
à certaines échelles les fluctuations deviennent non-linéaires,
que se forment les objets lumineux.
Nous sommes confrontés à un certain nombre
de problèmes fondamentaux, liés aux fluctuations
primordiales, et plus précisément:
- leur origine;
- leur type;
- leur spectre;
- leur amplitude;
- les processus qui peuvent les avoir modifiées.
Les modèles standard ne peuvent rien dire à propos de l'origine
des fluctuations.
En ce qui concerne le type des fluctuations
on peut les classer dans deux categories principales:
fluctuations de courbure (adiabatiques)
ou isocourbure (isothermes).
Dans le premier cas, toutes
les composantes (baryons, rayonnement, matière noire) fluctuent
en même temps; ce qui se traduit dans une
fluctuation du même ordre de la température du rayonnement:

Dans le cas des fluctuations d'isocourbure, au contraire,
la fluctuation change seulement la densité des baryons ou
d'une autre composante, et ne change pas la densité
d'énergie totale (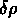 = 0).
Étant donné que la densité d'au moins une composante change,
et puisque
= 0).
Étant donné que la densité d'au moins une composante change,
et puisque 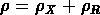 , cela signifie qu'on doit
avoir des fluctuations de
, cela signifie qu'on doit
avoir des fluctuations de 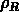 , c'est à dire de température;
mais on peut montrer que cette variation dans le cas où
, c'est à dire de température;
mais on peut montrer que cette variation dans le cas où
 est négligeable, d' où le nom de
fluctuations isothermes.
est négligeable, d' où le nom de
fluctuations isothermes.
L'évolution
des fluctuations peut être bien suivie dans le régime
linéaire, tandis que, quand les fluctuations deviennent faiblement
non-linéaires, on peut utiliser l'approximation de Zel'dovich,
qui décrit l'évolution du mode croissant des fluctuations.
C'est avec cette approximation que Zel'dovich a montré que dans le cadre
d'un univers à matière sombre chaude, il y a
formation de structures planes, les ``crêpes" ( pancakes).
Dans le régime non-linéaire, il faut recourir aux simulations
numériques, mais c'est en général avec
l'approximation de Zel'dovich qu'on crée les conditions initiales.
Dans le cas d'un univers infini et statique, Jeans a montré que seules les
fluctuations d'échelle supérieure à

où 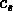 est la vitesse du son,
peuvent croître, avec une loi exponentielle en fonction du temps.
est la vitesse du son,
peuvent croître, avec une loi exponentielle en fonction du temps.
Cette échelle peut être derivée approximativement
en comparant le temps d'effondrement gravitationnel
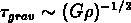 avec le temps caractéristique de la
propagation des ondes sonores
avec le temps caractéristique de la
propagation des ondes sonores 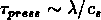 .
La condition pour que la gravitation puisse prévaloir sur la pression
est que
.
La condition pour que la gravitation puisse prévaloir sur la pression
est que  , c'est à dire
, c'est à dire
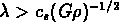 .
.
Dans un univers en expansion, il est clair que leur croissance
sera moins rapide.
Par exemple, si 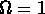 , la densité est donnée par
, la densité est donnée par

et les fluctuations suivent une loi de puissance:

Pour les perturbations de taille inférieure à celle de l'horizon,
on peut utiliser une approximation newtonienne.
On a deux modes possibles, l'un croîssant, l'autre decroîssant.
Pendant l' ère du rayonnement, les inhomogénéités
de densité des baryons ne peuvent pas
croître, mais celles de la matière non-baryonique
peuvent commencer à croître dès que l'Univers est dominé
par la matière.
Après le découplage entre matière et rayonnement, le contraste de
densité de la matière croît selon les relations suivantes:
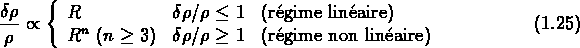
Dans la phase linéaire, 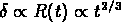 (environ)
aux échelles plus grandes que la longueur de Jeans
(environ)
aux échelles plus grandes que la longueur de Jeans 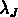 ,
tandis que les perturbations
aux échelles plus petites oscillent comme des ondes acoustiques.
,
tandis que les perturbations
aux échelles plus petites oscillent comme des ondes acoustiques.
En ce qui concerne l'amplitude et le spectre des fluctuations, les
modèles standard de Big Bang sont
encore une fois sans réponse et les observations du fond diffus, surtout
par COBE, sont encore plutôt incertaines pour donner des informations
fiables. L'amplitude est en général déduite des observations et imposée
au modèle. Le spectre des fluctuations primordiales est déduit
d'un certain nombre d'hypothèses.
Si l'on définit un champ de fluctuations de densité
non dimensionnel 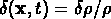 , on peut
écrire:
, on peut
écrire:

où les coefficients de Fourier 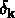 nous donnent
le spectre de puissance des fluctuations:
nous donnent
le spectre de puissance des fluctuations:

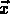 et
et 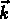 sont coordonnées comobiles; les coordonnées
physiques correspondantes sont
sont coordonnées comobiles; les coordonnées
physiques correspondantes sont 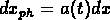 et
et 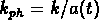 (
(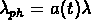 ).
).
Pour avoir des prédictions théoriques et pouvoir les comparer avec les
observations, il faut choisir un spectre de puissance donné. C'est
à ce niveau là que l'on introduit un certain nombre d'hypothèses.
Par exemple on peut supposer que les coefficients de Fourier 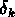 ont des phases aléatoires,
c'est à dire qu'on consière des fluctuations gaussiennes.
ont des phases aléatoires,
c'est à dire qu'on consière des fluctuations gaussiennes.
Si les fluctuations primordiales n'ont pas d'échelle privilegiée,
leur spectre de puissance peut être bien représenté par
une loi de puissance:

Si l'on fait l'hypothèse supplémentaire que l' amplitude des
fluctuations est la même quand leur longueur d'onde est égale à
l'horizon, alors n =1, et l'on obtient le spectre d'Harrison-Zel'dovich.
Il s'agit là bien évidemment d'hypothèses raisonnables dans les limites
de notre ignorance.
Mais les complications ne sont pas terminées: quand les fluctuations entrent
dans l'horizon, le spectre change à la suite de phénomènes
physiques qui dépendent du scénario choisi
(c'est ce que l'on verra dans la section suivante).
On peut alors écrire:
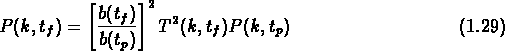
où 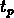 est un temps primordial aproprié et
est un temps primordial aproprié et 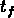 est le temps final
auquel les phénomènes qui modulent le spectre sont terminés,
est le temps final
auquel les phénomènes qui modulent le spectre sont terminés, 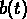 est
la loi de croissance linéaire des
fluctuations primordiales (qui dans un univers de Einstein-de Sitter
est proportionelle à
est
la loi de croissance linéaire des
fluctuations primordiales (qui dans un univers de Einstein-de Sitter
est proportionelle à 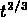 ), et
), et 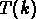 est la
fonction de transfert. Pour chaque scénario il faut connaître
cette fonction.
est la
fonction de transfert. Pour chaque scénario il faut connaître
cette fonction.




Next: Matière noire et
Up: Structures à grande
Previous: Les modèles de
alberto cappi
Wed Feb 5 10:43:08 MET 1997
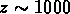 les fluctuations
à toutes les échelles étaient plus petites de
les fluctuations
à toutes les échelles étaient plus petites de 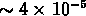 ), tandis que les fluctuations
de densité ont continué leur croissance; c'est dans cette phase, où
à certaines échelles les fluctuations deviennent non-linéaires,
que se forment les objets lumineux.
), tandis que les fluctuations
de densité ont continué leur croissance; c'est dans cette phase, où
à certaines échelles les fluctuations deviennent non-linéaires,
que se forment les objets lumineux.

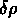 = 0).
Étant donné que la densité d'au moins une composante change,
et puisque
= 0).
Étant donné que la densité d'au moins une composante change,
et puisque 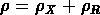 , cela signifie qu'on doit
avoir des fluctuations de
, cela signifie qu'on doit
avoir des fluctuations de 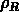 , c'est à dire de température;
mais on peut montrer que cette variation dans le cas où
, c'est à dire de température;
mais on peut montrer que cette variation dans le cas où
 est négligeable, d' où le nom de
fluctuations isothermes.
est négligeable, d' où le nom de
fluctuations isothermes.

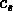 est la vitesse du son,
peuvent croître, avec une loi exponentielle en fonction du temps.
est la vitesse du son,
peuvent croître, avec une loi exponentielle en fonction du temps.
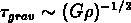 avec le temps caractéristique de la
propagation des ondes sonores
avec le temps caractéristique de la
propagation des ondes sonores 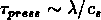 .
La condition pour que la gravitation puisse prévaloir sur la pression
est que
.
La condition pour que la gravitation puisse prévaloir sur la pression
est que  , c'est à dire
, c'est à dire
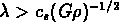 .
.
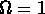 , la densité est donnée par
, la densité est donnée par


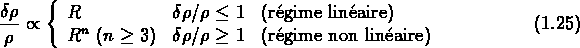
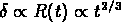 (environ)
aux échelles plus grandes que la longueur de Jeans
(environ)
aux échelles plus grandes que la longueur de Jeans 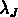 ,
tandis que les perturbations
aux échelles plus petites oscillent comme des ondes acoustiques.
,
tandis que les perturbations
aux échelles plus petites oscillent comme des ondes acoustiques.
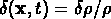 , on peut
écrire:
, on peut
écrire:

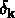 nous donnent
le spectre de puissance des fluctuations:
nous donnent
le spectre de puissance des fluctuations:

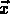 et
et 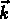 sont coordonnées comobiles; les coordonnées
physiques correspondantes sont
sont coordonnées comobiles; les coordonnées
physiques correspondantes sont 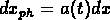 et
et 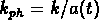 (
(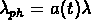 ).
).
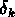 ont des phases aléatoires,
c'est à dire qu'on consière des fluctuations gaussiennes.
ont des phases aléatoires,
c'est à dire qu'on consière des fluctuations gaussiennes.

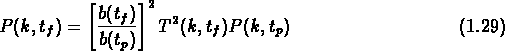
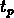 est un temps primordial aproprié et
est un temps primordial aproprié et 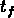 est le temps final
auquel les phénomènes qui modulent le spectre sont terminés,
est le temps final
auquel les phénomènes qui modulent le spectre sont terminés, 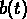 est
la loi de croissance linéaire des
fluctuations primordiales (qui dans un univers de Einstein-de Sitter
est proportionelle à
est
la loi de croissance linéaire des
fluctuations primordiales (qui dans un univers de Einstein-de Sitter
est proportionelle à 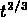 ), et
), et 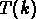 est la
fonction de transfert. Pour chaque scénario il faut connaître
cette fonction.
est la
fonction de transfert. Pour chaque scénario il faut connaître
cette fonction.