



Next: Distribution de matière
Up: Structures à grande
Previous: Des fluctuations à
Les inhomogénéités de densité peuvent
commencer à croître quand l'Univers devient dominé par la
matière (mais les baryons doivent attendre le découplage du rayonnement).
Nous avons brièvement
décrit comment l'on peut suivre l'évolution d'une fluctuation
de densité jusqu'à la formation d'un objet.
Mais l'élement essentiel qui discrimine les modèles possibles de
formation des structures est
le spectre des fluctuations, qui dépend du type de particules qui
sont présentes dans l'Univers.
Or, les observations montrent l'existence d'une composante significative
de matière non lumineuse, qui est difficilement explicable en termes
des baryons produits pendant la nucléosynthèse (voir la section suivante).
Ce fait a suggeré la présence de particules massives non-baryoniques.
En présence de matière non-baryonique,
le scénario change si l'on a à faire à des particules
qui étaient encore relativistes quand la masse dans l'horizon
est devenue comparable
à celle d'une galaxie (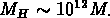 )
(tel le neutrino), ou qui étaient non relativistes (tel l' axion).
Donc nous avons un scénario avec matière noire chaude
( Hot Dark Matter, HDM ) ou froide ( Cold Dark Matter,
ou CDM ), et un cas intermédiaire de matière noire tiède
( Warm Dark Matter, WDM). Les spectres des fluctuations sont
différents: en figure (
)
(tel le neutrino), ou qui étaient non relativistes (tel l' axion).
Donc nous avons un scénario avec matière noire chaude
( Hot Dark Matter, HDM ) ou froide ( Cold Dark Matter,
ou CDM ), et un cas intermédiaire de matière noire tiède
( Warm Dark Matter, WDM). Les spectres des fluctuations sont
différents: en figure ( )
on montre sa forme typique en fonction de k.
)
on montre sa forme typique en fonction de k.
Pour un univers de HDM , le spectre est décrit par
(Bond & Szalay, 1983):
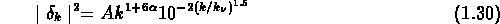
avec 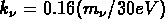 Mpc
Mpc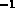 ,
et pour un univers de CDM (Peebles, 1983; Davis et al., 1985):
,
et pour un univers de CDM (Peebles, 1983; Davis et al., 1985):
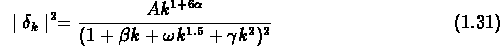
où 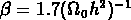 Mpc,
Mpc,
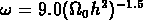 Mpc
Mpc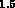 , et
, et
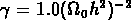 Mpc
Mpc .
.

Figure: Spectre de fluctuation dans les modèles de HDM et de
CDM (Kolb & Turner, 1990)
Dans le cadre d'un univers baryonique avec des fluctuations adiabatiques,
quand la température est supérieure à 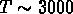 K,
matière et rayonnement interagissent fortement;
la pression des photons est telle que les fluctuations des baryons de
longueur d'onde inférieure à l'horizon ne
peuvent pas croître, et la masse de Jeans est beaucoup plus grande que
la masse dans l'horizon.
A
K,
matière et rayonnement interagissent fortement;
la pression des photons est telle que les fluctuations des baryons de
longueur d'onde inférieure à l'horizon ne
peuvent pas croître, et la masse de Jeans est beaucoup plus grande que
la masse dans l'horizon.
A 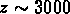 la température tombe suffisamment pour qu'il y ait
recombinaison entre protons et électrons, qui forment
les atomes d'hydrogène.
C'est à partir de ce moment que les fluctuations d'échelle
plus grande que la longueur de Jeans peuvent
commencer à croître.
la température tombe suffisamment pour qu'il y ait
recombinaison entre protons et électrons, qui forment
les atomes d'hydrogène.
C'est à partir de ce moment que les fluctuations d'échelle
plus grande que la longueur de Jeans peuvent
commencer à croître.
On trouve une masse de Jeans
de l'ordre de 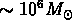 , qui correspond à la masse
d'un amas globulaire.
Mais il y a un effet dissipatif important qu'il faut considérer: c'est le
Silk damping. Le libre chemin moyen des photons augmente lorsque l'on
approche de la recombinaison et les photons diffusent en dehors des régions
plus denses; en conséquence, les fluctuations à petite longueur
d'onde sont effacées par la diffusion des photons.
L'échelle minimale à laquelle les fluctuations peuvent survivre est
, qui correspond à la masse
d'un amas globulaire.
Mais il y a un effet dissipatif important qu'il faut considérer: c'est le
Silk damping. Le libre chemin moyen des photons augmente lorsque l'on
approche de la recombinaison et les photons diffusent en dehors des régions
plus denses; en conséquence, les fluctuations à petite longueur
d'onde sont effacées par la diffusion des photons.
L'échelle minimale à laquelle les fluctuations peuvent survivre est

où 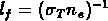 est le chemin libre moyen des photons dans
le plasma, et
est le chemin libre moyen des photons dans
le plasma, et 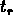 est l'epoque de la recombinaison.
Cela correspond à une masse minimale
est l'epoque de la recombinaison.
Cela correspond à une masse minimale

où 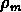 est la densité de la matière pendant la recombinaison.
On trouve
est la densité de la matière pendant la recombinaison.
On trouve 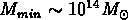 , c'est à dire qu'elle correspond
à la masse d'un amas de galaxies.
, c'est à dire qu'elle correspond
à la masse d'un amas de galaxies.
Pour des perturbations adiabatiques on a
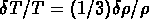 qui relie les fluctuations de température
(qui ne changent plus après la recombinaison) aux fluctuations de
densité d'énergie, qui continuent à croître
(proportionellement au facteur d'échelle si
qui relie les fluctuations de température
(qui ne changent plus après la recombinaison) aux fluctuations de
densité d'énergie, qui continuent à croître
(proportionellement au facteur d'échelle si 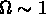 ).
Donc les limites sur les fluctuations de température sont
très contraignantes pour la formation de structures, qui demande
que
).
Donc les limites sur les fluctuations de température sont
très contraignantes pour la formation de structures, qui demande
que 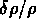 puisse devenir de l'ordre de 1.
puisse devenir de l'ordre de 1.
Dans le cas d'un univers dominé par la HDM , à cause du free streaming
des neutrinos, le spectre des fluctuations a une coupure à une longueur d'onde
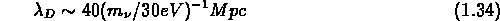
Par analogie au cas d'un univers purement baryonique, les premières
structures à se former ont une masse 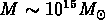 .
Ces structures ont une forme non-sphériques, dites
crêpes ( pancakes).
On parle donc de scénario top - down.
.
Ces structures ont une forme non-sphériques, dites
crêpes ( pancakes).
On parle donc de scénario top - down.
Pour la CDM , au contraire, le damping n'est pas important, et
l'on assiste à la formation d'objets à petite échelle,
c'est à dire aux échelles galactiques ou sous-galactiques.
On parle alors de scénario bottom-up.
Les régions de densité supérieure à la moyenne
ralentissent leur expansion par rapport à l'Univers, jusqu'au
moment où le collapse commence ( turnaround).
L'évolution des structures dans les différents scénarios a été
suivie par des simulations numériques par plusieurs auteurs, et comparée
avec les observations. Aucun de ces modèles ne semble pouvoir expliquer
toutes les observations, si l'on fait exception peut-être des
modèles hybrides.




Next: Distribution de matière
Up: Structures à grande
Previous: Des fluctuations à
alberto cappi
Wed Feb 5 10:43:08 MET 1997
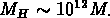 )
(tel le neutrino), ou qui étaient non relativistes (tel l' axion).
Donc nous avons un scénario avec matière noire chaude
( Hot Dark Matter, HDM ) ou froide ( Cold Dark Matter,
ou CDM ), et un cas intermédiaire de matière noire tiède
( Warm Dark Matter, WDM). Les spectres des fluctuations sont
différents: en figure (
)
(tel le neutrino), ou qui étaient non relativistes (tel l' axion).
Donc nous avons un scénario avec matière noire chaude
( Hot Dark Matter, HDM ) ou froide ( Cold Dark Matter,
ou CDM ), et un cas intermédiaire de matière noire tiède
( Warm Dark Matter, WDM). Les spectres des fluctuations sont
différents: en figure (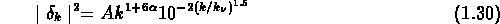
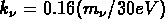 Mpc
Mpc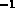 ,
et pour un univers de CDM
,
et pour un univers de CDM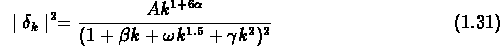
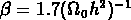 Mpc,
Mpc,
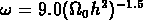 Mpc
Mpc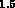 , et
, et
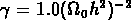 Mpc
Mpc .
.

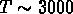 K,
matière et rayonnement interagissent fortement;
la pression des photons est telle que les fluctuations des baryons de
longueur d'onde inférieure à l'horizon ne
peuvent pas croître, et la masse de Jeans est beaucoup plus grande que
la masse dans l'horizon.
A
K,
matière et rayonnement interagissent fortement;
la pression des photons est telle que les fluctuations des baryons de
longueur d'onde inférieure à l'horizon ne
peuvent pas croître, et la masse de Jeans est beaucoup plus grande que
la masse dans l'horizon.
A 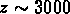 la température tombe suffisamment pour qu'il y ait
recombinaison entre protons et électrons, qui forment
les atomes d'hydrogène.
C'est à partir de ce moment que les fluctuations d'échelle
plus grande que la longueur de Jeans peuvent
commencer à croître.
la température tombe suffisamment pour qu'il y ait
recombinaison entre protons et électrons, qui forment
les atomes d'hydrogène.
C'est à partir de ce moment que les fluctuations d'échelle
plus grande que la longueur de Jeans peuvent
commencer à croître.
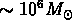 , qui correspond à la masse
d'un amas globulaire.
Mais il y a un effet dissipatif important qu'il faut considérer: c'est le
Silk damping. Le libre chemin moyen des photons augmente lorsque l'on
approche de la recombinaison et les photons diffusent en dehors des régions
plus denses; en conséquence, les fluctuations à petite longueur
d'onde sont effacées par la diffusion des photons.
L'échelle minimale à laquelle les fluctuations peuvent survivre est
, qui correspond à la masse
d'un amas globulaire.
Mais il y a un effet dissipatif important qu'il faut considérer: c'est le
Silk damping. Le libre chemin moyen des photons augmente lorsque l'on
approche de la recombinaison et les photons diffusent en dehors des régions
plus denses; en conséquence, les fluctuations à petite longueur
d'onde sont effacées par la diffusion des photons.
L'échelle minimale à laquelle les fluctuations peuvent survivre est

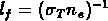 est le chemin libre moyen des photons dans
le plasma, et
est le chemin libre moyen des photons dans
le plasma, et 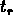 est l'epoque de la recombinaison.
Cela correspond à une masse minimale
est l'epoque de la recombinaison.
Cela correspond à une masse minimale

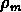 est la densité de la matière pendant la recombinaison.
On trouve
est la densité de la matière pendant la recombinaison.
On trouve 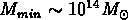 , c'est à dire qu'elle correspond
à la masse d'un amas de galaxies.
, c'est à dire qu'elle correspond
à la masse d'un amas de galaxies.
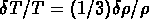 qui relie les fluctuations de température
(qui ne changent plus après la recombinaison) aux fluctuations de
densité d'énergie, qui continuent à croître
(proportionellement au facteur d'échelle si
qui relie les fluctuations de température
(qui ne changent plus après la recombinaison) aux fluctuations de
densité d'énergie, qui continuent à croître
(proportionellement au facteur d'échelle si 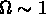 ).
Donc les limites sur les fluctuations de température sont
très contraignantes pour la formation de structures, qui demande
que
).
Donc les limites sur les fluctuations de température sont
très contraignantes pour la formation de structures, qui demande
que 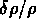 puisse devenir de l'ordre de 1.
puisse devenir de l'ordre de 1.
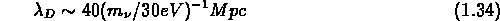
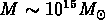 .
Ces structures ont une forme non-sphériques, dites
crêpes ( pancakes).
On parle donc de scénario top - down.
.
Ces structures ont une forme non-sphériques, dites
crêpes ( pancakes).
On parle donc de scénario top - down.