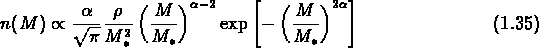
Le scénario standard prévoit que les structures que nous voyons dans l'Univers à l'heure actuelle se sont formeés à partir des fluctuations gaussiennes primordiales par aggrégation gravitationnelle.
Dans ce cadre, supposant qu'il n'y ait pas de coupure aux petites échelles, et que la formation des structures ait lieu suivant des processus hiérarchiques, Press et Schechter (1974) ont déduit une expression de la fonction de multiplicité:
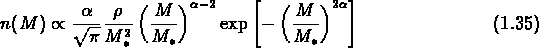
où
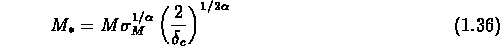
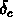est le contraste de densité au dessus duquel on a
la formation des structures, et 
.
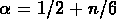A vrai dire la démonstration de Press et Schechter n'est pas
formellement parfaite; un facteur 2 est ajouté ad hoc
sinon seulement la moitié de la masse se retrouverait
sous la forme d'objets virialisés. Mais d'autres auteurs retrouvent
cette loi (Cole & Kaiser, 1989), qui décrit bien également les
résultats des simulations numériques.
De plus, Schechter (1976) a déduit de cette expression la fonction de luminosité des galaxies:
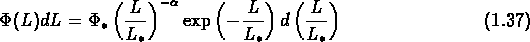
Cette ``loi de Schechter" constitue une très bonne description de la fonction de luminosité observée des galaxies, qui semble donc être universelle, même si les divers types morphologiques paraissent montrer des différences.
Grâce à la fonction de luminosité il est possible par exemple d'estimer la densité moyenne de matière visible qui se trouve dans les galaxies:
où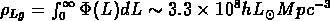 
est la luminosité moyenne par
unité de volume due aux galaxies; la masse peut être calculée à
partir des courbes de rotation des galaxies spirales ou en appliquant le
théorème du viriel aux galaxies elliptiques.
On trouve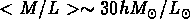 
et donc 
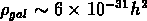g cm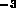
, ce qui implique 
.
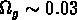Dans le cas des amas de galaxies, on trouve un rapport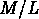 
de
l'ordre de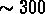 
qui, multiplié par la densité moyenne de lumière,
donne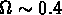 
. C'est ce genre de résultat qui
est à l'origine du problème de la matière noire (Zwicky, 1933).
Il est clair qu'en considérant seulement la matière
baryonique produite dans la phase de la nucleosynthèse
(
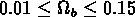) il est
difficile d'expliquer un rapport aussi élevé.
Mais il est aussi clair qu'on est loin de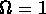 
,
la valeur derivée de l'inflation. Pour concilier
la valeur observée avec la valeur théorique, il faut supposer
que la matière lumineuse n'est pas distribuée comme la
matière noire. En fait
Kaiser (1984, 1986), pour expliquer la différence entre la
fonction de corrélation des
amas
et celle
de galaxies, a suggeré que les galaxies se forment seulement
là où la fluctuation de densité est supérieure à
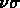fois la densité moyenne: c'est ce qu'on a appelé
la formation biaisée des galaxies.
Dans ce cas, Kaiser a démontré que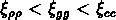 
.
La conséquence de la formation biaisée des galaxies est donc que
la matière lumineuse est plus corrélée de la matière
noire, et l'on a:
et
où N répresente les comptages de galaxies et le facteur de biais b
est généralement estimé entre 1 et 2.5 (cela dépend des
objets considérés). Les comptages de galaxies dans le catalogue
CfA donnent 
à une échelle de 8 
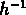Mpc ; on a alors
Cette relation est importante car elle permet de normaliser le spectre
des fluctuations primordiales utilisé dans les modèles:
l'amplitude A de ces spectres est choisie de manière telle
que la variance de la masse actuelle soit égal à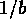 
à
l'échelle de 8 
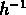Mpc .
Kashlinsky (1987, 1991) a essayé de généraliser ce scénario de formation biaisée des structures, calculant des prédictions pour les corrélations croisées entre systèmes divers; j'en discuterai un peu plus dans le chapitre dedié aux groupes de galaxies.
Toutefois, les problèmes ne sont pas totalement résolus: en effet, le modèle classique de la CDM prévoit un fonction de corrélation des amas à peu près 5 fois celle de la distribution de masse et seulement deux fois celle des galaxies (White et al. 1987).