



Next: Conclusions
Up: Structures à grande
Previous: Distribution de matière
Now symmetry and consistency are convertible terms:
--thus Poetry and Truth are one.
Edgar Allan Poe, Eureka
Nous avons décrit l'évolution de fluctuations de densité
primordiales dans le cadre des modèles standard de Big Bang
(Friedman-Lemaître). Jusqu'à présent, il n'y a
aucune évidence observationnelle en désaccord avec ces
modèles, ce qui est remarquable. Mais nous avons vu qu'ils ne peuvent nous
donner aucune indication quant à l'origine des fluctuations.
En plus, ils ne peuvent nous donner aucune réponse
à trois problèmes majeurs.
- Le problème de l'horizon: à
chaque instant t, on ne peut pas avoir de rapports de causalité
entre des régions qui sont séparés par
une distance supérieure au rayon de l'horizon,
défini par:

A l'époque de la recombinaison (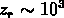 et
et 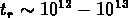 s), le rayon de l'horizon était
approximativement
s), le rayon de l'horizon était
approximativement 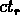 ; cela implique que quand on observe le rayonnement
fossile dans deux directions separées par une distance angulaire
supérieure à
; cela implique que quand on observe le rayonnement
fossile dans deux directions separées par une distance angulaire
supérieure à 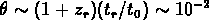 , les deux régions
n'ont pas eu la possibilité de communiquer: comment
expliquer alors l'extrême degré d'isotropie du rayonnement fossile?
, les deux régions
n'ont pas eu la possibilité de communiquer: comment
expliquer alors l'extrême degré d'isotropie du rayonnement fossile?
- Le problème de la ``platitude" ( flatness).:
la valeur de
 , comme celle de
, comme celle de 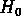 , varie dans le temps.
On peut écrire sa valeur au redshift z en fonction de sa valeur
, varie dans le temps.
On peut écrire sa valeur au redshift z en fonction de sa valeur
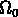 à notre époque:
à notre époque:
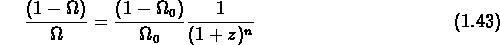
où n=3 pour un univers de matière (w=0) et n=4 pour un univers
de rayonnement (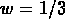 ).
Or, nous avons remarqué que les prédictions de la nucléosynthèse nous
donnent une valeur
).
Or, nous avons remarqué que les prédictions de la nucléosynthèse nous
donnent une valeur 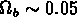 ; les observations des amas de galaxies
nous donnent
; les observations des amas de galaxies
nous donnent 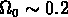 ; et en présence de biais, il est bien
possible d'avoir
; et en présence de biais, il est bien
possible d'avoir
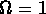 . Mais sa valeur exacte n'est pas importante. Ce qui importe
est que
. Mais sa valeur exacte n'est pas importante. Ce qui importe
est que 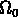 n'est pas très loin de l'unité, ce qui implique,
selon la formule (
n'est pas très loin de l'unité, ce qui implique,
selon la formule ( ),
qu'au temps de Planck (
),
qu'au temps de Planck (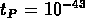 sec) il devait être encore
plus proche de l'unité:
sec) il devait être encore
plus proche de l'unité:

Il semble vraiement improbable que ce soit dû au hasard, et qu'il est
plus logique d'imaginer qu' soit toujours été égal à
1; mais alors il faut chercher une explication physique à cette
valeur.
soit toujours été égal à
1; mais alors il faut chercher une explication physique à cette
valeur.
- Le problème des monopôles magnetiques: selon les théories de
Grande Unification (GUT), on devrait observer un très grand nombre
de monopôles, qui représentent des défauts topologiques formés à
l'époque de la rupture de symétrie.
L'idée de l'inflation (Guth, 1981) représente une tentative
de solution à cet ensemble des problèmes, et je crois qu'il est
utile de décrire ses caractéristiques principales.
Je présenterai
la théorie de l'inflation dans le cadre d'un changement de phase
(bien qu'il ne soit pas nécessaire).
Les GUT nous disent que l'unification des
forces électromagnetique et électro-faible a lieu à une température 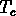 supérieure à
supérieure à 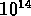 GeV, correspondant à une époque où
l'Univers avait un âge de
GeV, correspondant à une époque où
l'Univers avait un âge de 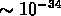 s.
s.
Quand la température tombe au dessous de 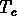 , le premier modèle
d'inflation prévoit par exemple
la rupture de symétrie SU(5), qui devient
, le premier modèle
d'inflation prévoit par exemple
la rupture de symétrie SU(5), qui devient
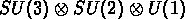 . Cette transition implique qu'un
quantité scalaire
. Cette transition implique qu'un
quantité scalaire 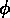 (le champ de Higgs) prend une valeur
non nulle.
(le champ de Higgs) prend une valeur
non nulle.
Le tenseur énergie-impulsion du champ a une densité d'energie

et une pression P

Le potentiel 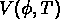 est fonction de la température:
quand la température
est fonction de la température:
quand la température 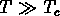 , il est caractérisé
par un seul minimum, qui se trouve à
, il est caractérisé
par un seul minimum, qui se trouve à 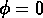 .
Mais quand la température tombe en dessous de
.
Mais quand la température tombe en dessous de 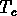 se forme un minimum secondaire, à
se forme un minimum secondaire, à 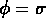 .
.
Les équations de Friedman deviennent:
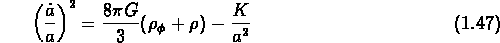
et
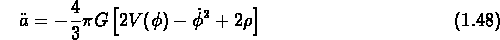
On trouve alors l'equation de l'évolution du champ 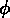 (equation de
Klein-Gordon):
(equation de
Klein-Gordon):
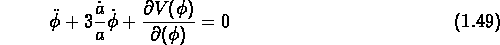
Si dans une région supposée isotrope et homogène en expansion,
décrite par la métrique de Robertson-Walker, la température
tombe en dessous de 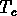 , l'évolution suivra
l'equation (
, l'évolution suivra
l'equation ( ). Puisque le terme de courbure est négligeable,
et que
). Puisque le terme de courbure est négligeable,
et que 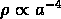 , on a
, on a

Si l'on suppose que 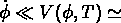 const,
la solution correspond au modèle de Einstein-de Sitter
précédemment décrit avec
const,
la solution correspond au modèle de Einstein-de Sitter
précédemment décrit avec

où
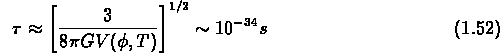
Le potentiel, qui est plat dans tous les modèles d'inflation,
évolue en trois phases: il y a un effondrement
de la barrière entre 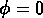 et
et 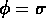 , ensuite un lent
``roulement", et finalement le champ scalaire a des oscillations cohérentes
en correspondance du minimum du potentiel.
, ensuite un lent
``roulement", et finalement le champ scalaire a des oscillations cohérentes
en correspondance du minimum du potentiel.
Ces oscillations libèrent l'énergie contenue dans le potentiel
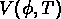 , et causent une augmentation de la température.
L'oscillation est désamorcée par la production de particules
nouvelles qui remplissent à nouveau l'Univers, vidé par
l'expansion exponentielle.
L'idée centrale est qu'il y aurait eu une phase d'expansion
exponentielle de l'Univers causée par une transition de phase.
Pendant cette époque, dite phase de de Sitter,
l'énergie du vide aurait été la composante
dominante de la densité d'énergie de l'Univers.
Cette expansion se serait produite après le temps de Planck (
, et causent une augmentation de la température.
L'oscillation est désamorcée par la production de particules
nouvelles qui remplissent à nouveau l'Univers, vidé par
l'expansion exponentielle.
L'idée centrale est qu'il y aurait eu une phase d'expansion
exponentielle de l'Univers causée par une transition de phase.
Pendant cette époque, dite phase de de Sitter,
l'énergie du vide aurait été la composante
dominante de la densité d'énergie de l'Univers.
Cette expansion se serait produite après le temps de Planck (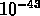 s).
s).
Cette hypothèse permet d'expliquer en même temps
l'isotropie présentée par des régions différentes de l'Univers, une
valeur pour  voisine de 1,
et le motif pour lequel on ne trouve pas de monopôles magnetiques,
qui devraient être
très nombreux selon les prédictions des théories GUT.
En plus, l'inflation peut produire un spectre des
fluctuations initiales gaussiennes qui correspond au spectre de
Harrison-Zel'dovich.
Pendant l'inflation, la longueur d'onde propre des fluctuations
augmente, et devient égale au rayon de Hubble
voisine de 1,
et le motif pour lequel on ne trouve pas de monopôles magnetiques,
qui devraient être
très nombreux selon les prédictions des théories GUT.
En plus, l'inflation peut produire un spectre des
fluctuations initiales gaussiennes qui correspond au spectre de
Harrison-Zel'dovich.
Pendant l'inflation, la longueur d'onde propre des fluctuations
augmente, et devient égale au rayon de Hubble 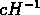 au temps
au temps
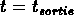 :
:

Après l'inflation, pendant l'ère du rayonnement, le fluctuations
rentrent dans l'horizon au temps 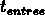 (fig.
(fig. ).
).

Figure: Échelle physique des fluctuations et du rayon d'Hubble en fonction
de 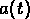 (Kolb & Turner, 1990)
(Kolb & Turner, 1990)
A cette époque, on peut suivre l'évolution des fluctuations dans
le cadre des modèles standard.
C'est grâce à l'inflation que les petites fluctuations quantiques
auraient pu devenir assez grandes pour faire naître les inhomogénéités
que nous observons aujourd'hui.
Plusieurs versions différentes de cette idée initiale ont été
proposées, et à vrai dire, chacune présente quelque problème.
Une question importante est par exemple comment il y a eu la transition entre
l'ère de l'inflation et l'ère du rayonnement.
Mais que l'inflation se révele finalement vraie ou fausse, cela ne
touche pas la validité des modèles de Big Bang, qui découlent de
la théorie de la Relativité générale et qui se réferent à une
époque de l'Univers ultérieure à l'inflation.




Next: Conclusions
Up: Structures à grande
Previous: Distribution de matière
alberto cappi
Wed Feb 5 10:43:08 MET 1997

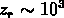 et
et 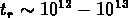 s), le rayon de l'horizon était
approximativement
s), le rayon de l'horizon était
approximativement 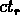 ; cela implique que quand on observe le rayonnement
fossile dans deux directions separées par une distance angulaire
supérieure à
; cela implique que quand on observe le rayonnement
fossile dans deux directions separées par une distance angulaire
supérieure à 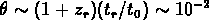 , les deux régions
n'ont pas eu la possibilité de communiquer: comment
expliquer alors l'extrême degré d'isotropie du rayonnement fossile?
, les deux régions
n'ont pas eu la possibilité de communiquer: comment
expliquer alors l'extrême degré d'isotropie du rayonnement fossile?
 , comme celle de
, comme celle de 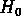 , varie dans le temps.
On peut écrire sa valeur au redshift z en fonction de sa valeur
, varie dans le temps.
On peut écrire sa valeur au redshift z en fonction de sa valeur
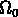 à notre époque:
à notre époque:
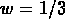 ).
Or, nous avons remarqué que les prédictions de la nucléosynthèse nous
donnent une valeur
).
Or, nous avons remarqué que les prédictions de la nucléosynthèse nous
donnent une valeur 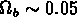 ; les observations des amas de galaxies
nous donnent
; les observations des amas de galaxies
nous donnent 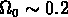 ; et en présence de biais, il est bien
possible d'avoir
; et en présence de biais, il est bien
possible d'avoir
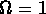 . Mais sa valeur exacte n'est pas importante. Ce qui importe
est que
. Mais sa valeur exacte n'est pas importante. Ce qui importe
est que 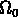 n'est pas très loin de l'unité, ce qui implique,
selon la formule (
n'est pas très loin de l'unité, ce qui implique,
selon la formule (![]() ),
qu'au temps de Planck (
),
qu'au temps de Planck (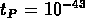 sec) il devait être encore
plus proche de l'unité:
sec) il devait être encore
plus proche de l'unité:

 soit toujours été égal à
1; mais alors il faut chercher une explication physique à cette
valeur.
soit toujours été égal à
1; mais alors il faut chercher une explication physique à cette
valeur.
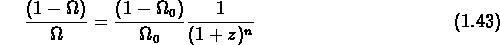
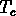 supérieure à
supérieure à 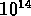 GeV, correspondant à une époque où
l'Univers avait un âge de
GeV, correspondant à une époque où
l'Univers avait un âge de 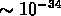 s.
s.
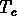 , le premier modèle
d'inflation prévoit par exemple
la rupture de symétrie SU(5), qui devient
, le premier modèle
d'inflation prévoit par exemple
la rupture de symétrie SU(5), qui devient
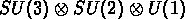 . Cette transition implique qu'un
quantité scalaire
. Cette transition implique qu'un
quantité scalaire 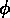 (le champ de Higgs) prend une valeur
non nulle.
(le champ de Higgs) prend une valeur
non nulle.


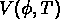 est fonction de la température:
quand la température
est fonction de la température:
quand la température 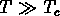 , il est caractérisé
par un seul minimum, qui se trouve à
, il est caractérisé
par un seul minimum, qui se trouve à 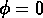 .
Mais quand la température tombe en dessous de
.
Mais quand la température tombe en dessous de 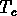 se forme un minimum secondaire, à
se forme un minimum secondaire, à 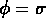 .
.
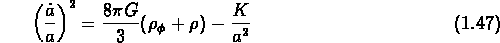
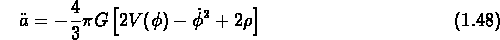
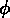 (equation de
Klein-Gordon):
(equation de
Klein-Gordon):
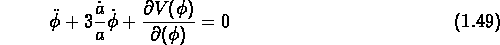
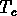 , l'évolution suivra
l'equation (
, l'évolution suivra
l'equation (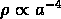 , on a
, on a

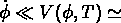 const,
la solution correspond au modèle de Einstein-de Sitter
précédemment décrit avec
const,
la solution correspond au modèle de Einstein-de Sitter
précédemment décrit avec

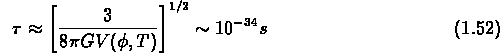
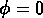 et
et 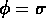 , ensuite un lent
``roulement", et finalement le champ scalaire a des oscillations cohérentes
en correspondance du minimum du potentiel.
, ensuite un lent
``roulement", et finalement le champ scalaire a des oscillations cohérentes
en correspondance du minimum du potentiel.
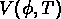 , et causent une augmentation de la température.
L'oscillation est désamorcée par la production de particules
nouvelles qui remplissent à nouveau l'Univers, vidé par
l'expansion exponentielle.
L'idée centrale est qu'il y aurait eu une phase d'expansion
exponentielle de l'Univers causée par une transition de phase.
Pendant cette époque, dite phase de de Sitter,
l'énergie du vide aurait été la composante
dominante de la densité d'énergie de l'Univers.
Cette expansion se serait produite après le temps de Planck (
, et causent une augmentation de la température.
L'oscillation est désamorcée par la production de particules
nouvelles qui remplissent à nouveau l'Univers, vidé par
l'expansion exponentielle.
L'idée centrale est qu'il y aurait eu une phase d'expansion
exponentielle de l'Univers causée par une transition de phase.
Pendant cette époque, dite phase de de Sitter,
l'énergie du vide aurait été la composante
dominante de la densité d'énergie de l'Univers.
Cette expansion se serait produite après le temps de Planck (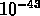 s).
s).
 voisine de 1,
et le motif pour lequel on ne trouve pas de monopôles magnetiques,
qui devraient être
très nombreux selon les prédictions des théories GUT.
En plus, l'inflation peut produire un spectre des
fluctuations initiales gaussiennes qui correspond au spectre de
Harrison-Zel'dovich.
Pendant l'inflation, la longueur d'onde propre des fluctuations
augmente, et devient égale au rayon de Hubble
voisine de 1,
et le motif pour lequel on ne trouve pas de monopôles magnetiques,
qui devraient être
très nombreux selon les prédictions des théories GUT.
En plus, l'inflation peut produire un spectre des
fluctuations initiales gaussiennes qui correspond au spectre de
Harrison-Zel'dovich.
Pendant l'inflation, la longueur d'onde propre des fluctuations
augmente, et devient égale au rayon de Hubble 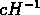 au temps
au temps
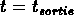 :
:

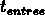 (fig.
(fig.
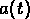 (Kolb & Turner, 1990)
(Kolb & Turner, 1990)