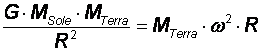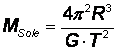|
|
|
|
|
|
|
|
|
L’aberrazione annua della luce
Claudio
Elidoro
|
L’analisi del fenomeno dell’aberrazione della luce
può essere una ghiotta occasione per fare qualche ‘piccolo conto’ astronomico con il semplice aiuto di una
calcolatrice. Un primo calcolo che possiamo fare prende direttamente le mosse dal
valore dell’aberrazione della luce trovato da Bradley.
Partendo dal valore di 20,50 secondi d’arco possiamo ottenere facilmente
quanto vale il rapporto tra la velocità con la quale la Terra si muove
intorno al Sole e la velocità della luce. Per fare questo è sufficiente
calcolare il valore della tangente di un angolo con ampiezza di 20,50
secondi. Una qualunque calcolatrice scientifica ci permette
di ottenere che: v / c = 0,000099387. Da questo risultato possiamo ricavare v semplicemente assumendo per c il valore di 299800 km/s. La nostra fidata calcolatrice ci suggerisce che v = 29,79 km/s. Spulciando nei libri di astronomia possiamo verificare
che il valore ottenuto è quello giusto. E questo ci spinge a continuare i
nostri calcoli. Ammettiamo per comodità di calcolo che l’orbita (C) percorsa dalla Terra sia circolare. Poiché
sappiamo che quest’orbita viene percorsa in 365
giorni (cioè 31.536.000 secondi) possiamo ricavare la sua lunghezza. Avremo
dunque: C = v x t = 29,79 x 31536000 = A questo punto siamo anche in grado di calcolare il
raggio di questa orbita, vale a dire la distanza Terra-Sole (detta anche Unità
Astronomica): R = C /
2p = Dato che anche questo valore si dimostra in ottimo
accordo con quanto riportano i testi astronomici, possiamo anche lasciare che
la smania da calcoli ci prenda la mano e puntiamo decisi in alto. Obiettivo: calcolare
la massa del Sole. Il modello che consideriamo è ancora quello della
Terra in orbita circolare intorno al Sole. In tale situazione l’attrazione
gravitazionale è controbilanciata dalla forza centrifuga. In formule:
Il termine a sinistra del segno uguale nella (1) è
l’espressione dell’attrazione gravitazionale descritta dalla Legge di
gravitazione universale. G è la costante di gravitazione universale ed R la distanza tra le due masse (Sole e Terra).
Nel termine di destra (interpretabile come F = m x a ) compare l’espressione dell’accelerazione nel
moto circolare uniforme. Riscriviamo la (1)
eliminando in entrambi i membri MTerra ed esprimendo la forza centrifuga in termini di
periodo (T) anziché
di velocità angolare (w) tenendo conto che
w = 2p / T. Otteniamo così:
Da cui:
Ricorriamo ancora alla calcolatrice, facendo però
molta attenzione alle unità di misura. Per agevolare il compito dei più pigri (e per dare
modo ai più volonterosi di verificare le proprie
scelte) riportiamo per esteso le grandezze da impiegare nel calcolo,
sottolineando che si è fatto ricorso ad unità di misura cgs: R @ 1,49 x Lasciamo il compito del calcolo al lettore e ci
permettiamo unicamente di suggerire il risultato finale apparso sul display
della nostra calcolatrice: MSole = 1,96 x Il fidato testo di astronomia già consultato in
precedenza confermerà ancora una volta la bontà della nostra approssimazione. A questo punto, però, è bene fermarsi e lasciar
riposare la fidata calcolatrice.
|