|
|
|
|
|
|
|
|
|
Il principio di indeterminazione
Annibale
D’Ercole
|
Consideriamo un raggio
luminoso emesso da una sorgente, ad esempio un laser. Com’è noto, la luce del
laser è composta da un’onda elettromagnetica monocromatica, ovvero da oscillazioni
del campo elettrico (e magnetico) di una precisa lunghezza d’onda l
che si propagano lungo la direzione del raggio luminoso. La Fig. 1 rappresenta una “istantanea” a
un determinato tempo del valore del campo elettrico lungo la direzione di propagazione,
con l’ampiezza A che indica il
massimo valore (positivo o negativo) assunto dal campo stesso. Questo
andamento può essere descritto semplicemente dalla funzione armonica seno: Y(x) = Asin(kx) (1) Il
numero d’onda k è definito come k = 2p/l.
Y(x)
è ovviamente una funzione periodica: in particolare, essa si annulla nei
punti x = np/k,
dove n=0,1,2,… assume solo valori
interi. Questi punti vengono detti “nodi”, e sono individuati in Fig. 1 [livello base] dall’intersezione
di Y(x)
con l’asse x.
È
interessante vedere che succede quando due onde interferiscono, ovvero si
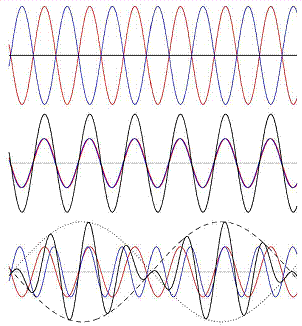
sovrappongono durante il loro percorso. Lo schema in alto nella Fig. 3 rappresenta due onde armoniche di
pari ampiezza e lunghezza d’onda (le due curve rosse e blu) sfasate in
maniera tale che i massimi di una si trovano in corrispondenza dei minimi
dell’altra. In questo caso la somma delle due onde dà luogo a un’onda
risultante ovunque nulla: in altre parole le due onde interferiscono
distruttivamente. Lo schema intermedio in Fig.
3 illustra l’interferenza di due onde di pari ampiezza e lunghezza d’onda nel
caso in cui i massimi e i minimi di una siano posizionati in corrispondenza
dei massimi e minimi dell’altra. In questo caso le due onde interferiscono
ovunque positivamente dando luogo a un’onda di stessa lunghezza d’onda, ma di
ampiezza doppia (indicata dalla linea nera spessa). Più interessante è il
caso mostrato dallo schema in basso di Fig.
3 in cui viene illustrata l’interferenza tra due onde di pari ampiezza, ma
con lunghezze d’onda (e dunque numeri d’onda) un poco diverse. L’onda
risultante è data da Y(x) = Asin(k1x) +
Asin(k2x) = 2Acos[0.5(k1-k2)x]sin[0.5(k1+k2)x], (2) dove l’ultimo
passaggio è stato ottenuto in base alle formule di prostaferesi. In Fig. 3 le curve rossa e blu
rappresentano le onde con numero d’onda k1
e k2,
mentre la curva nera spessa illustra l’andamento di Y(x). Il fattore
sinusoidale in Eq. (2)
rappresenta un’onda molto simile a quelle originali, con un numero d’onda
dato dalla media dei valori delle due onde. Il fattore cosinusoidale ha una
lunghezza d’onda lc = 2p/Dk, con Dk =
k1-k2;
esso dunque varia assai più lentamente dell’altro e può essere considerato
come un’ampiezza variabile. Come risultante abbiamo dunque un’onda che ha
circa la stessa lunghezza, ma la cui ampiezza varia con x. La linea punteggiata in Fig.
3 rappresenta la curva 2Acos[0.5(k1-k2)x], mentre la linea
tratteggiata è simmetrica di questa rispetto all’asse x. Y(x)
si svolge tra le due, toccando alternativamente l’una o l’altra.
Sottolineiamo come, contrariamente al caso dell’onda armonica, qui le
oscillazioni tendono a raggrupparsi in una serie di “pacchetti”, ognuno dei
quali ha una estensione Dx = lc/2; ne segue dunque la
relazione DxDk=p.
(3) Riprenderemo
tra poco questa importante relazione. Per il momento torniamo alla sorgente
luminosa dell’esempio da cui siamo partiti. Supponiamo questa volta che tale
sorgente rimanga accesa per un tempo brevissimo, in modo da emettere un
impulso luminoso simile al flash delle macchine fotografiche. Se a un dato
istante potessimo osservare le oscillazioni del campo elettrico dell’impulso
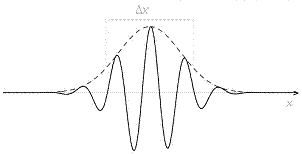
luminoso, vedremmo qualcosa di simile a quanto rappresentato in Fig. 4.
Fig. 4. Pacchetto
d’onda gaussiano. Le
oscillazioni sono assenti a grandi valori di x perché la radiazione non vi è ancora giunta, ma sono assenti
anche “alle spalle” dell’impulso luminoso perché nessuna radiazione è stata
più emessa successivamente. Dunque tale impulso è descritto da un unico
pacchetto d’onda simile a quello mostrato in Fig.
4, e che può essere descritto come la sovrapposizione di un gran numero (al
limite infinito) di onde armoniche di diversa ampiezza e lunghezza d’onda,
tali per cui esse interferiscono distruttivamente ovunque, tranne che in una
ristretta regione dove è localizzato l’impulso luminoso (teorema di Fourier).
Una misura dell’estensione Dx di questa regione è
data, ad esempio, dalla larghezza a mezza altezza della “campana” che sagoma
il profilo del pacchetto (si veda la Fig.
4). Si può dimostrare che anche per questo generico pacchetto vale una
relazione simile all’Eq. (3): DxDk=p.
(3) dove Dk rappresenta
l’intervallo di valori dei numeri d’onda assunti dalle onde armoniche che
compongono il pacchetto. Dunque, tanto più la posizione del pacchetto è
localizzata, ovvero il pacchetto è stretto, maggiore è il numero di armoniche
(coprendo, nel loro insieme, un intervallo Dk maggiore). Al
contrario, un pacchetto molto esteso è composto da un minor numero di
armoniche: al limite, esso coincide con una singola armonica nel caso di
un’estensione infinita. E
veniamo, finalmente, al collegamento tra la meccanica quantistica e quanto
abbiamo esposto finora. Nel 1905, nel corso dei suoi studi sull’effetto
fotoelettrico, Einstein introdusse il concetto di fotone (vedi in questa
rubrica nel n. 2, 2000, p. 63). Ci sono dei fenomeni – come l’effetto
fotoelettrico, appunto – che possono essere compresi solo abbandonando
l’interpretazione ondulatoria classica della radiazione e ammettendo che essa
possa essere descritta come uno “sciame” di fotoni, microscopiche particelle
di energia E = hn
(qui h rappresenta la costante di
Plank e n
la frequenza della radiazione). Già in fisica classica era noto che la radiazione
possiede una quantità di moto – o impulso – che può eventualmente essere
ceduto alle particelle con cui la radiazione si trovi a interagire (un
esempio spettacolare è dato dal gas delle code cometarie rosse che viene
soffiato via dalla radiazione solare che trasferisce ad esso parte del
proprio impulso). Dagli esperimenti risulta che l’impulso p associato ad un singolo fotone è
pari a p = hn/c = h/l. Le
esperienze di laboratorio di interferenza degli elettroni descritte nella sezione
precedente (il livello base di questa rubrica) hanno mostrato che
l’ambivalenza onda-particella, già scoperta per la radiazione, deve valere
anche per la materia. Per questo motivo, nel 1924 Louis-Victor Pierre de
Broglie (1892-1987) ipotizzò, in analogia al fotone, che anche l’elettrone
potesse essere descritto da una funzione oscillante, la funzione d’onda Y(x), la cui lunghezza
d’onda, per un elettrone di impulso p,
sia l = h/p. Cosa fosse a
oscillare in relazione ad un elettrone rimase oscuro fino al 1927, quando Max
Born (1882-1970) propose che Y(x)
(o meglio, il suo modulo quadrato) rappresenti la probabilità di trovare
l’elettrone nel punto x: in questa
interpretazione, nell’esperienza dell’interferenza elettronica l’onda di
probabilità di un singolo elettrone “attraversa” entrambe le fenditure e le
frange luminose si formano nei punti dove è massima la probabilità di trovare
un elettrone, ovvero dove la funzione d’onda interferisce costruttivamente. Tuttavia,
in un qualunque esperimento, un elettrone è confinato in un volume limitato
all’interno della strumentazione adoperata. Di conseguenza, la sua funzione
d’onda non può essere descritta da una singola armonica di lunghezza d’onda l,
che invece si estende in tutto lo spazio. Piuttosto, Y(x) deve essere rappresentata da un
pacchetto d’onda come quello illustrato in Fig.
4. Deve dunque valere anche in questo caso l’Eq.
(4) che, tenuto conto della relazione tra impulso e lunghezza d’onda, può
essere scritta come DxDp »
h, (4) con h = h/2p.
Questa formula rappresenta il celebre principio di indeterminazione enunciato
da Werner Heisemberg nel 1927 e stabilisce che non è possibile misurare con
grande precisione contemporaneamente l’impulso e la posizione di una
particella dal momento che, se l’incertezza Dx sulla posizione è
piccola, l’incertezza Dp sull’impulso deve essere grande, e viceversa. |