|
|
|
|
|
|
|
|
|
Il principio di indeterminazione
Annibale
D’Ercole
|
Com’è
noto, la luce è dovuta alle oscillazioni di un campo elettrico (e magnetico)
che si propaga nello spazio analogamente alle onde sulla superficie del mare.
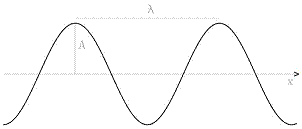
Essa è caratterizzata dalla lunghezza d’onda, ovvero dalla distanza che
separa due massimi (creste) o due minimi (ventri) successivi (Fig. 1).
Fig.
1. Onda armonica. La natura ondulatoria della luce
venne evidenziata nei primi anni dell’Ottocento da Thomas Young (1773-1829)
tramite un famoso esperimento che qui ricordiamo brevemente, in quanto
descritto in dettaglio in questa stessa rubrica nel fascicolo scorso (n. 4,
2008, p. 33). Supponiamo di dirigere un fascio
luminoso verso uno schermo. Se interponiamo un diaframma con due fenditure,
sullo schermo si ottiene una serie di immagini luminose inframezzate da
regioni che rimangono scure. Queste frange
di interferenza sono caratteristiche dei fenomeni ondulatori. In effetti,
la radiazione che supera le fenditure si propaga di nuovo in tutte le
direzioni. Di conseguenza, la luce proveniente da una fenditura si sovrappone
a quella proveniente dall’altra fenditura. In particolare, le chiazze luminose sullo schermo si verificano là
dove i massimi delle due onde si sovrappongono, dando luogo a una
interferenza positiva e dunque all’immagine luminosa. Nei punti sullo schermo
dove la cresta di un’onda si sovrappone al ventre dell’altra si ha
un’interferenza distruttiva: la somma delle due onde è nulla e nessuna
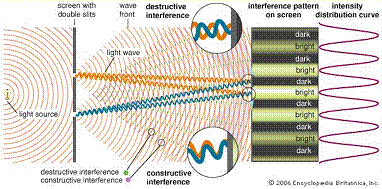
illuminazione si verifica in quei punti (Fig.
2).
Fig.
2. Schema dell’esperimento di Young. Oltre un secolo dopo Young,
l’esperimento venne ripetuto utilizzando un fascio di elettroni al posto di
quello luminoso e utilizzando un cristallo (l’analogo del diaframma) e un
rivelatore di particelle (l’analogo dello schermo). Ci si aspetterebbe che
gli elettroni che attraversano le due fenditure proseguano in direzione
rettilinea andando a colpire la regione di schermo proprio di fronte ad esse
e formando dunque l’analogo di due sole chiazze luminose. Al contrario, anche
in questo caso si ottiene una figura di diffrazione che rivela l’aspetto
ondulatorio degli elettroni. Ma, se nel caso della radiazione ad oscillare
sono i campi elettrici e magnetici, cos’è che oscilla nel caso di un
elettrone? L’ipotesi maggiormente (ma non unanimemente) accettata è che
dobbiamo abbandonare il principio classico di causalità in base al quale il
moto di una particella in ciascun istante è determinato unicamente dal suo moto
precedente, così da poter calcolare esattamente la posizione della particella
stessa. Al contrario, esperimenti e condizioni iniziali identici non
producono necessariamente misurazioni identiche e dunque è possibile fare
solo previsioni di tipo statistico. L’interferenza tra gli elettroni si verifica perché
l’elettrone ha una certa quota di
probabilità di passare attraverso una fenditura e un’altra quota di probabilità di
passare dall’altra fenditura. Pertanto
una particella è descritta da una funzione Y(x) che indica la probabilità della
particella di trovarsi in un determinato punto x. Si dimostra che Y(x) è di tipo ondulatorio, come le funzioni che descrivono altri
tipi di onda (elettromagnetiche, sonore, marine), e viene dunque chiamata funzione d’onda. L’esperimento di interferenza viene
quindi interpretato dalla meccanica quantistica nel modo seguente: la
funzione d’onda di una singola particella “attraversa” le due fessure e
successivamente interferisce analogamente a come farebbe un’onda elettromagnetica
classica. Nei punti sullo schermo dove si verificano interferenze costruttive
è maggiore la probabilità di trovare la particella. Werner
Karl Heisenberg (1901-1976) ha formalizzato l’intrinseca indeterminatezza
della posizione dell’elettrone nel suo famoso principio di
indeterminazione che si scrive nel seguente modo: DxDp
» h. Qui Dx rappresenta l’incertezza nella posizione della
particella e Dp
quella sul suo
impulso p = mv, dove m e v rappresentano, rispettivamente, la massa e la velocità delle particella.
h
= h/2p, con h pari alla costante di Plank. Intuitivamente possiamo
ragionare come segue: per osservare una bilia di vetro e misurarne la
posizione dobbiamo illuminarla; in questo caso l’energia del raggio luminoso
è trascurabile e non ha effetto sul moto e dunque sulla velocità della bilia.
Se però investiamo un elettrone con dei fotoni, questi ultimi, avendo
un’energia paragonabile a quella dell’elettrone, ne deflettono la traiettoria
alterando l’impulso dell’elettrone di una quantità Dp. Una maggiore illuminazione
permette una più precisa determinazione della posizione (ovvero una riduzione
di Dx), ma peggiora la misura
dell’impulso, con un incremento di Dp. Una seconda formulazione del
principio di indeterminazione coinvolge l’energia della particella. Sappiamo che la meccanica
quantistica associa fotoni di energia E
= hn a
onde elettromagnetiche di frequenza n.
Per misurare questa frequenza è necessario contare il numero di oscillazioni
compiute dall’onda in un intervallo di tempo Dt fissato. Questo intervallo non dovrebbe essere più
breve del periodo dell’onda, ovvero del tempo impiegato a compiere
un’oscillazione completa. Se infatti si misura solo parte dell’oscillazione,
la frequenza e dunque l’energia del fotone, può essere conosciuta solo con
una certa approssimazione DE: minore è l’intervallo temporale Dt, maggiore è l’incertezza DE. Più precisamente, il principio di
indeterminazione stabilisce che DEDt
» h e questa relazione vale non solo
per i fotoni ma anche per le particelle materiali. Quindi, indipendentemente
dalla precisione degli strumenti adoperati, non è possibile determinare con
esattezza l’energia di particelle in esperimenti in cui esse si creano e
annichilano in tempi brevissimi. Il principio di indeterminazione ha
implicazioni profonde. Si consideri, ad esempio, una regione di spazio vuota.
Per la fisica classica essa è una sorta di contenitore inerte privo di
qualunque interesse. La meccanica quantistica, tuttavia, stabilisce che lo
spazio non può essere mai completamente vuoto. Un’assenza di campi
elettromagnetici equivarrebbe, in termini quantistici, a un’assenza di
fotoni, ovvero a fotoni con energia esattamente nulla. Il principio di
indeterminazione nella forma DEDt
» h
impone, invece,
un’incertezza sull’energia dei fotoni che deve fluttuare di una quantità DE; questa violazione della legge
della conservazione dell’energia non può perdurare a lungo e i fotoni tornano
a unirsi, annichilendosi a vicenda dopo un tempo Dt. Fotoni con energia maggiore sopravvivono per tempi
minori. Quel che abbiamo detto per il campo elettromagnetico vale per
qualunque campo ψ(x,t) e quindi nel vuoto si creano coppie di
particelle e antiparticelle di ogni tipo (p.e. elettroni e antielettroni) che
poi si annichilano a vicenda. Queste particelle vengono chiamate virtuali.
A differenza di quelle reali, non possono essere osservate direttamente con
un rivelatore di particelle. Tuttavia, è possibile misurare i loro effetti
indiretti, come nel caso dell’effetto Casimir, che abbiamo trattato in questa
rubrica nel 2004 (n. 4, p. 40). Si noti che il principio di
indeterminazione porta ad un conflitto con la teoria della relatività
generale che stabilisce che lo spazio (o, meglio, lo spazio-tempo) si incurva
in prossimità di oggetti massicci. Ora, in base a quanto abbiamo detto, nel
vuoto possono comparire particelle molto energetiche, a patto che il loro
tempo di vita sia molto breve. Ma, in virtù dell’equivalenza tra massa ed
energia, a queste particelle è associata una massa m = DE/c2 (dove c
è la velocità della luce) in grado di curvare localmente lo spazio. Lo spazio
vuoto sembrerebbe dunque essere “schiumoso” piuttosto che liscio, come
assunto dalla relatività generale. Non bisogna credere che il
principio di indeterminazione, data la sua stranezza, sia confinato solo nei
libri di fisica o all’interno dei laboratori scientifici. Al contrario, pur
senza rendercene conto, lo incontriamo in oggetti di uso quotidiano che
sfruttano il cosiddetto effetto tunnel. Classicamente, una pallina in
fondo a una buca non ne può fuoriuscire, a meno di non fornirle un’energia
cinetica sufficiente. Dal punto di vista quantistico, tuttavia, se la
particella è confinata in una buca molto stretta (ovvero se l’incertezza Dx sulla sua posizione è molto
piccola), l’incertezza Dp del suo impulso, e dunque della sua
velocità, è molto grande. Quindi la particella ha una certa probabilità di
trovarsi con un’energia sufficiente a uscire dalla buca, anche se la sua
energia media non basterebbe a superare la barriera. Otteniamo lo stesso
risultato utilizzando anche la seconda formulazione del principio di
indeterminazione. Si può infatti affermare che, su un intervallo di tempo Dt sufficientemente breve, la
fluttuazione energetica DE della pallina è tale da permetterle
di fuoriuscire. L’effetto tunnel è utilizzato nei
dispositivi elettrici ordinari per far “saltare” gli elettroni aldilà di
barriere di potenziale elettrico altrimenti insuperabili. Ad esempio, ogni connessione fra cavi elettrici
effettuata meccanicamente (morsetti) comporta conduzione per effetto tunnel.
Infatti, ogni conduttore esposto all’aria si ricopre rapidamente di uno
strato di ossido, per cui fili intrecciati o connessi con viti,
morsetti etc. (esempio: le usuali lampadine avvitate nella loro sede),
presentano strati isolanti fra le giunzioni. La corrente elettrica può fluire
grazie all’effetto tunnel. Questo effetto è altresì alla base di molti
dispositivi elettronici quali diodi, memorie flash e microscopi. Ricordiamo
infine che l’effetto tunnel consente anche il verificarsi del fenomeno della
radioattività. |