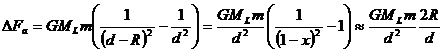|
|
|
|
|
|
|
|
|
La forza mareale
Annibale
D’Ercole
|
Per capire
come la Luna provochi le maree terrestri consideriamo la forza di gravità che
il nostro satellite esercita sulla Terra. Per semplicità fissiamo l’attenzione
su due punti particolari della superficie terrestre, entrambi posti sulla
linea congiungente i due corpi celesti (indicati con le lettere A e B nel
pannello a della Fig. 1). Se d è
la distanza tra i centri di Terra e Luna ed R è il raggio della Terra,
possiamo scrivere la forza esercitata dalla Luna su due particelle di massa m
poste nei punti A e B come:
dove G è
la costante gravitazionale e ML la massa
della Luna. In ogni punto della superficie la forza mareale
è determinata dalla differenza tra la forza di gravità della Luna esercitata
in quel punto e quella esercitata al centro della Terra. Dunque la forza di
marea nel punto A della Fig. 1 è
data da:
dove x = R/d
e l’ultimo passaggio è stato ottenuto in base al fatto che R << d. (Sviluppando
l’espressione in parentesi si ottiene (2x - x2) / (1 - 2x + x2);
dal momento che x è molto minore di 1, abbiamo x2 << x <<
1, e la formula precedente può approssimarsi come ~2x = 2R/d.) Come si può notare, la forza mareale è una frazione 2R/d = 0,034 della forza con cui
la Luna attrae a sé la Terra. Si
può facilmente dimostrare che DFb = -DFa.
La Fig. 1 in effetti mostra che,
mentre i vettori che rappresentano la gravità lunare sono tutti diretti verso
il centro del nostro satellite, la forza mareale
“stira” la Terra simmetricamente rispetto al suo centro lungo la direzione
Terra-Luna, producendo due rigonfiamenti mareali.
Questa stessa figura mostra anche che la forza mareale
diventa compressiva lateralmente – dove si creano le basse maree – favorendo
ulteriormente la formazione dei rigonfiamenti. Data la posizione simmetrica
di questi ultimi, si producono due alte maree in un periodo di 24 ore e 50
minuti. In effetti, nel tempo che la Terra impiega a fare un giro completo su
se stessa, la Luna compie un piccolo tratto lungo la sua orbita; dunque, la
Terra deve ruotare un poco più di 360° affinché un dato punto su di essa
torni a stare in direzione della Luna: questo spiega perché il periodo delle
due maree è maggiore di 24 ore. In
verità, i rigonfiamenti mareali non sono
direttamente allineati con la Luna come mostrato in Fig. 1. Questo avviene perché il periodo di rotazione terrestre
è inferiore al periodo orbitale del nostro satellite e la Luna tende a
rimanere “indietro”, come mostrato in Fig.
2. Questo disallineamento produce alcuni effetti oggi ben misurabili, come il
rallentamento della rotazione terrestre e l’allontanamento della Luna.
Vediamo in dettaglio ognuno di questi effetti.
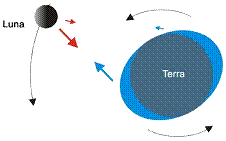
Fig. 2 – Uno
dei due rigonfiamenti mareali è più vicino dell’altro
alla Luna. La forza gravitazionale esercitata dalla Luna su di essi è dunque
diversa e si realizza una coppia torcente che tende a rallentare la rotazione
terrestre. Rallentamento della rotazione terrestre La Fig. 2 mostra come i due rigonfiamenti
mareali interagiscono gravitazionalmente
con la Luna: il rigonfiamento più vicino tende, come abbiamo detto, a sopravanzare
il nostro satellite, ma ne subisce l’azione frenante a causa del richiamo
gravitazionale (freccia azzurra lunga). Naturalmente la Luna agisce anche sul
rigonfiamento più distante (freccia azzurra corta) stimolando, in questo
caso, un’accelerazione; tuttavia, a causa della maggiore distanza,
quest’ultimo effetto è inferiore al primo e il risultato netto è un
rallentamento della rotazione dell’ellissoide mareale.
Dunque, parti diverse della Terra, ruotando più velocemente dei
rigonfiamenti, attraversano i rigonfiamenti stessi. Pertanto, strati
superficiali sempre diversi della Terra vengono continuamente “stirati” e
deformati. L’attrito che si genera in questo processo dissipa in calore parte
dell’energia cinetica di rotazione terrestre; il nostro pianeta riduce
progressivamente la sua velocità di rotazione e il giorno si allunga al tasso
attuale di 0,0016 secondi ogni secolo. Allontanamento della Luna Abbiamo
visto che la rotazione dei due lobi mareali
terrestri viene rallentata dal nostro satellite; per il principio di azione e
reazione è altresì vero che la Luna tende ad essere “trainata” da questo
rigonfiamento (freccia rossa lunga nella Fig.
2). Questo provoca un aumento progressivo della distanza Terra-Luna. Per capire
il perché di questo effetto procediamo per passi temporali successivi.
Inizialmente la Luna è su un’orbita stabile con velocità u a distanza r dalla Terra: questo significa
che, in un riferimento rotante con la Luna, l’azione gravitazionale
esercitata dalla Terra, Fg = GMm/r2, è bilanciata dalla forza centrifuga Fc = Mmu2/r, dove G è la costante gravitazionale ed
M ed m sono, rispettivamente, la massa della Terra e della Luna. A causa del
traino del rigonfiamento mareale più vicino, la
Luna tende ad accrescere la sua velocità; Fc
pertanto aumenta, prevalendo sulla gravità terrestre e spingendo la Luna ad
una distanza maggiore. Nell’allontanarsi dalla Terra il nostro satellite
accresce la propria energia potenziale U = -GMm/r e
deve pertanto diminuire la sua energia cinetica T = 0.5mu2
poiché, durante questa fase, l’energia totale E = U + T rimane costante
(analogamente a quello che succede quando lanciamo un sasso in aria). La Luna
dunque si assesta su una nuova orbita stabile ad r’ > r, e u’ < u.
L’intero processo a questo punto riprende provocando un ulteriore nuovo
allontanamento. Naturalmente,
la descrizione del fenomeno in passi discreti successivi rappresenta un
artificio operato a scopo illustrativo; in realtà l’allontanamento della Luna
avviene in maniera continua al tasso odierno di 3-4 centimetri all’anno. Vale
la pena sottolineare che, come è stato accennato nel livello base, questo
fenomeno può essere spiegato in termini di conservazione del momento angolare
totale, piuttosto che in termini di forze e di energia, come abbiamo fatto
qui. |