|
|
|
|
|
|
|
|
|
La forza mareale
Annibale
D’Ercole
|
Immaginiamo
un uomo che si lanci da un trampolino con il cosiddetto stile “a candela”,
ovvero rimanendo in posizione verticale per tutta la durata del tuffo, con la
testa in alto e i piedi in basso. L’effetto più ovvio della gravità terrestre
è naturalmente quello di far cadere il tuffatore in acqua. Vi è però un
secondo effetto, assai meno evidente, legato al fatto che la gravità
diminuisce all’aumentare della distanza dal centro della Terra: i piedi sono
“tirati” in basso più intensamente di quanto non lo sia la testa, che è più
distante dal suolo. Il nostro tuffatore subisce pertanto una sorta di
“stiramento” dovuto al differente valore della gravità tra testa e piedi:
questo effetto viene detto “effetto mareale”, e la
sua causa (la differenza di gravità) “forza mareale”.
Dal momento che l’altezza del tuffatore è trascurabile rispetto al raggio
terrestre, la differenza di gravità tra testa e piedi è parimenti
trascurabile rispetto al valore della gravità sulla superficie terrestre: il
tuffatore, dunque, non corre alcun serio rischio di essere stirato. Al contrario, in campo astronomico vi
sono casi in cui la forza mareale gioca un ruolo di
primo piano. Una stella che passasse sufficientemente vicina a un buco nero,
ad esempio, potrebbe essere stirata fino a “sfarinarsi” del tutto. Non
mancano poi esempi di effetti mareali nei dintorni
e all’interno della nostra Galassia. Attorno alla Via Lattea orbitano alcune
piccole galassie satellite; due di queste, la Piccola e la Grande Nube di
Magellano, visibili dall’emisfero sud, subiscono una costante emorragia di gas
dando luogo alla cosiddetta Corrente Magellanica,
una “striscia” di gas che si estende tra le Nubi e la Galassia lungo un arco
di 180° sulla volta celeste e che deriva da un’interazione mareale con la Via Lattea. Un’altra piccola galassia
satellite, Sag deg (Sagittarius Dwarf Elliptical Galaxy), sta precipitando all’interno della nostra
Galassia e, benché mantenga ancora un certo grado di coerenza, si trova in un
avanzato stato di “smembramento” proprio a causa dell’azione mareale della Via Lattea. Ma non è necessario alzare gli occhi al
cielo per assistere ad effetti mareali. Infatti le
familiari maree che si susseguono periodicamente e che coinvolgono grandi
masse d’acqua (oceani, mari e grandi laghi) sono proprio l’effetto della
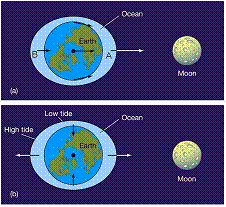
forza mareale esercitata dalla Luna sulla Terra (Fig. 1).
Fig. 1 – (a) Forza di gravità della Luna
esercitata sulla Terra. (b) Forza mareale della
Luna ottenuta sottraendo alla gravità esercitata in ogni punto la gravità
esercitata al centro (la scala è magnificata rispetto ad (a) per meglio
evidenziare la forza mareale). La figura è inesatta
in quanto in realtà l’asse dei due rigonfiamenti mareali
non è esattamente in direzione della Luna, perché il periodo orbitale di
quest’ultima è maggiore del periodo di rotazione terrestre. (Copyright 2005, Pearson Prentice Hall, Inc.) Similmente
al tuffatore che viene “stirato” dal campo mareale
terrestre, la Terra viene “stirata” dal campo mareale
della Luna. Gli oceani tendono allora a formare due lobi, uno in direzione
della Luna, ed uno in direzione opposta, come mostrato in Fig. 1. Dunque, un punto sulla Terra,
compiendo un giro ogni 24 ore, sperimenta in un giorno due alte maree (quando
attraversa i due rigonfiamenti) e due basse maree. (In verità il periodo è un
poco superiore alle 24 ore. Si veda il livello avanzato.) I livelli
d'innalzamento delle acque si fanno sentire particolarmente vicino alle coste
e possono raggiungere anche i 15 metri (come nel celebre caso dell'isolotto
di Mont Saint-Michel, sulla costa
settentrionale della Francia), mentre in mare aperto non toccano il metro di
altezza. Anche la crosta solida terrestre subisce un doppio rigonfiamento la
cui altezza, tuttavia, è di soli 10 centimetri. L’alternarsi delle maree crea attrito tra
gli oceani e il fondo oceanico ed anche tra strati diversi della crosta
terrestre. Questo attrito dissipa in calore parte dell’energia cinetica di
rotazione del nostro pianeta; la velocità angolare della Terra dunque
diminuisce, ed il giorno si allunga. Attualmente l’allungamento del giorno è
di appena 16 milionesimi di secondi all’anno. Tuttavia l’effetto cumulativo
nel corso del tempo è stato tutt’altro che trascurabile. Una prima
evidenza deriva dallo studio di alcuni coralli fossili di 400 milioni di anni
di età. I coralli presentano anelli annuali di crescita similmente a quello
che accade per gli alberi. Nei coralli, tuttavia, è possibile osservare una
serie fittissima di striature che rappresentano anelli di crescita
giornalieri. Mentre effettivamente i coralli odierni mostrano 365 anelli
giornalieri compresi tra due anelli annuali, nei coralli fossili se ne
contano 400. Questo indica che vi erano più giorni in un anno, e dunque che
la velocità di rotazione terrestre allora era maggiore, con la durata del
giorno pari a 22 ore e 45 minuti. Spingendosi più in là nel passato, si
ottengono durate ancora più brevi, come testimoniato dalle rocce sedimentarie
antiche. L’alternarsi delle maree ha rilasciato su tali rocce microscopiche
striature, tramite le quali è stato calcolato che 900 milioni di anni or sono
la durata della rotazione terrestre era di sole 18 ore e 10 minuti. Connesso al rallentamento della rotazione
terrestre c’è l’allontanamento della Luna. Con buona approssimazione,
possiamo considerare il sistema Terra-Luna come isolato (su cui, cioè, non
agiscono forze esterne), con la Luna che orbita attorno alla Terra. È noto che
in un sistema isolato si conserva il momento angolare (ne abbiamo discusso
nelle “Spigolature Astronomiche” del «Giornale di Astronomia» n. 2 del 2008).
Tale conservazione impone che, se un sistema rotante si espande, la sua
velocità di rotazione diminuisce. Una pattinatrice sul ghiaccio ruota su se
stessa sempre più velocemente man mano che porta le braccia vicino al corpo e
viceversa (e questo senza che nessuna forza intervenga su di essa). Lo stesso
principio si applica al sistema Terra-Luna. In passato, quando la Luna era
più vicina alla Terra, l’intero sistema ruotava più velocemente. Ma al
diminuire della rotazione terrestre la Luna, a seguito della conservazione
del momento angolare, è stata “costretta” a porsi a distanze sempre maggiori.
Tornando all’analogia con la pattinatrice, possiamo considerare la Terra come
il suo corpo e la Luna come le sue mani: allontanando le mani, il corpo
rallenta. L’odierna
velocità di allontanamento del nostro satellite è di circa 3,8 centimetri
l’anno. Questa misura è resa possibile dagli specchi lasciati sulla Luna
dagli astronauti delle missioni Apollo. Si invia un impulso laser verso
questi specchi e si misura il tempo di ritorno (con la precisione di un
milionesimo di milionesimo di secondo); la metà di tale tempo moltiplicata
per la velocità della luce (~ 300.000 km/s) dà la distanza della Luna con un
margine di errore di circa 1 mm. Ripetendo questa misura negli anni si è
ottenuta la velocità di allontanamento. Consideriamo infine un effetto dovuto
alla forza mareale esercitata dalla Terra sulla
Luna. È il ben noto fenomeno della rotazione sincrona: il nostro satellite
compie un giro su se stesso nello stesso tempo impiegato per compiere una
rivoluzione attorno alla Terra. Il risultato, come sappiamo, è che la Luna
mostra sempre la stessa “faccia” verso la Terra. In passato, in effetti, la
Luna ruotava più velocemente, ma nel tempo la sua rotazione è diminuita per
motivi analoghi a quelli che hanno determinato il rallentamento della
rotazione terrestre. Oggi, mostrando la Luna sempre lo stesso lato verso la
Terra, non vi è più alcuna tendenza ad una rotazione relativa tra le
protuberanze mareali della superficie lunare e il
corpo centrale del nostro satellite. Pertanto, in assenza di ogni ulteriore
dissipazione per attrito, il periodo di rotazione della Luna rimane
“agganciato” a quello di rivoluzione. |