La magnitudine stellare
Claudio Elidoro

 

Anche un’occhiata distratta al cielo stellato ci può permettere di verificare che non tutte le stelle brillano con la medesima intensità. Non dobbiamo stupirci, dunque, se il concetto di magnitudine stellare ci giunge fin dall’antichità.

Già nel secondo secolo a.C. il grande Ipparco di Nicea, compilando il suo catalogo astronomico, introdusse una classificazione delle stelle tenendo conto della loro brillantezza, classificazione che venne mantenuta anche da Tolomeo verso la fine del secondo secolo d.C. La scala scelta dai due astronomi prevedeva che le stelle più luminose venissero collocate nella prima classe, quelle un po’ meno luminose nella seconda e, giù giù, fino a quelle appena visibili a occhio nudo, collocate nella sesta classe. Erano tempi in cui ancora non esisteva neppure il dubbio che le stelle potessero essere a differenti distanze da noi, ma tutte venivano considerate alla medesima distanza, fissate su quell’enorme sfera che costituiva la volta celeste. Logico concludere, sotto questa ipotesi, che una maggiore quantità di luce significasse anche una maggiore dimensione. E così avvenne che lo stesso termine usato per identificare le classi di Ipparco (magnitudo) sottolineasse proprio questa constatazione.

Banale sottolineare come si trattasse di una scala soggettiva e tutt’altro che precisa, legata com’era all’acutezza visiva dell’osservatore, alla sua capacità valutativa e alle condizioni osservative. Fortunatamente erano tempi nei quali l’inquinamento luminoso ancora non esisteva, ma è evidente che prima o poi sarebbe stato indispensabile dare alla classificazione una connotazione più scientifica. Ci provò inizialmente William Herschel (1738 – 1822), annotando come una stella di prima magnitudine fosse circa 100 volte più brillante di una di sesta, ma la soluzione definitiva fu opera di Norman Robert Pogson (1829 – 1891). Utilizzando un primitivo fotometro ebbe la conferma di quanto Herschel aveva segnalato e questo lo indusse nel 1857 a proporre di fissare “esattamente” quel rapporto in 100:1. Una tale scelta avrebbe non solo consentito di mantenere la scala di luminosità in vigore, ma anche di inquadrare la classificazione in una definizione matematicamente esatta.

La risposta dell’occhio umano agli stimoli luminosi, però, non è di tipo lineare. Negli stessi anni in cui Pogson avanzava la sua proposta, Fechner e Weber dimostrarono che nella percezione visiva la sensazione era proporzionale al logaritmo dello stimolo. Questo, applicato al caso delle stelle, significava che la magnitudine era proporzionale al logaritmo dell’illuminamento, vale a dire:

 

                               (1)

 

Fissata dunque una stella di riferimento caratterizzata da illuminamento Io e magnitudine mo si poteva definire la magnitudine di un’altra stella caratterizzata da illuminamento I come:

 

               (2)

 

Applicando alla (2) la convenzione proposta da Pogson si determina il valore di k ottenendo:

 

                         (3)

 

L’espressione (3) è dunque nota come Formula di Pogson e descrive il legame tra la magnitudine di una stella e il flusso luminoso che giunge al nostro occhi.

Ci sono un paio di aspetti poco felici nella scelta di Pogson di fare in modo di restare fedele alla classificazione di Ipparco. Il primo è che, contrariamente a quanto il senso comune potrebbe suggerire, la luminosità maggiore corrisponde a numeri più bassi, con la spiacevole conseguenza che per il profano alcuni diagrammi in cui compaiono le magnitudini non sono di immediata lettura. Un secondo aspetto è che per oggetti particolarmente luminosi si è costretti a ricorrere ai numeri negativi. 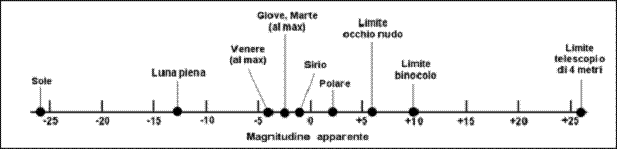Sirio, per esempio, ha una magnitudine di – 1.4 mentre per il Sole si deve raggiungere il valore di – 26.74.

Nella fig. 1 sono riportati i valori di magnitudine di alcuni corpi celesti. È un grafico indicativo ed estremamente semplificato, ma è certamente in grado di dare un’idea dell’estensione di questa scala.

 

 Fig. 1.

 

Si è già sottolineato che per gli antichi non si poneva il problema della distanza di una stella. Per noi non è più così: sappiamo infatti che le stelle non sono a uguale distanza da noi e questa semplice constatazione ci impone una riflessione. La magnitudine che noi rileviamo non dà alcuna informazione sulla effettiva quantità di luce irradiata da una stella, ma si limita ad indicare che al nostro occhio giunge più (o meno) energia luminosa che non da un’altra. Non siamo in grado, cioè, di distinguere se la stella più luminosa emette maggiore flusso luminoso o è semplicemente più vicina. Per questo motivo ci si riferisce alle magnitudini definite da Pogson con il termine di magnitudini apparenti, intendendo con questo aggettivo il fatto che le luminosità considerate sono quelle che appaiono agli occhi dell’osservatore.

E’ dunque necessario definire una nuova grandezza che dia una corretta misura del rilascio di energia luminosa di una stella, svincolandola dagli effetti della distanza. Questa grandezza è la magnitudine assoluta (M), definita come la magnitudine che la stella avrebbe se venisse osservata da una distanza fissata (arbitrariamente) in 10 parsec (32.6 anni luce).

L’espressione che lega tra loro la magnitudine apparente (m), quella assoluta (M) e la distanza (d) espressa in parsec è la seguente:

 

   (4)

 

Per ovvie ragioni di spazio il nostro discorso deve concludersi qui, ma è inevitabilmente destinato a riaffacciarsi su queste pagine per affrontare alcuni temi fino ad ora lasciati in disparte. Non è stato detto, ad esempio, a cosa possa praticamente servire la relazione (4). Non è stato fatto nessun accenno alla diversità di colore che caratterizza le stelle e al suo possibile significato fisico. Abbiamo inoltre parlato di magnitudini riferendoci esclusivamente alla rilevazione della luce visibile, ma non è detto che tutta l’emissione di una stella cada necessariamente in quella regione dello spettro elettromagnetico. Temi cruciali, come si può ben intuire, e che sarà dunque necessario approfondire.

 

Home
Spigolature

 

Livello
Avanzato