|
|
|
|
|
|
|
|
|
Il caos
Annibale D'Ercole
Osservatorio
Astronomico - Bologna
|
L’andamento
caotico di un sistema può essere utilmente illustrato dal problema,
opportunamente semplificato, dell’evoluzione di una popolazione all’interno di
un determinato ecosistema. Supponiamo che in qualche luogo provvisto di
consistenti risorse alimentari vi sia una colonia di
prede, ad esempio conigli. Questi conigli richiamano inevitabilmente dei
predatori, ad esempio volpi, il cui numero, se la caccia è buona, è destinato
ad aumentare. Dal momento che il numero dei figli è proporzionale a quello
dei genitori, il numero di volpi xn+1 all’istante tn+1
è proporzionale al numero xn all’istante
precedente tn: xn+1
= k xn, (1) dove k è una costante. D’altra parte una crescita
illimitata di volpi non è possibile perché i conigli non sarebbero
sufficienti a sfamarle tutte; dunque il numero di volpi tende a diminuire quando diventa troppo grande. È ragionevole
porre il tasso di riduzione xn+1/xn
proporzionale a xn. Assumendo per
semplicità la stessa costante di proporzionalità k, possiamo scrivere L’andamento generale della popolazione
nel tempo è dato dalla combinazione delle equazioni (1) e (2): xn+1=
kxn(1-xn). (3) L’equazione (3), detta equazione
logistica, è stata introdotta nel 1845
da P.F. Verhust ed è
stata utilizzata, ad esempio, per spiegare la dinamica di crescita di una
popolazione e in alcuni modelli di crescita di un capitale nel tempo.
Tornando alle nostre volpi, ci si aspetterebbe che il numero di predatori (e di
prede) fornito dall’equazione logistica si stabilizzi su un valore di
equilibrio, oppure che oscilli con regolarità
attorno a tale valore. La realtà, come vedremo, è più complessa.
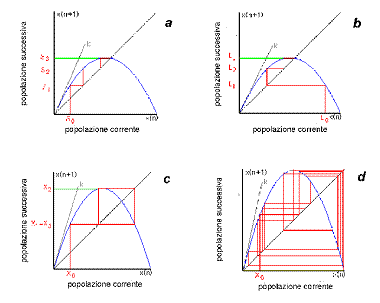
L’asse
x della fig. 3a rappresenta l’ammontare della popolazione della generazione
corrente, mentre l’asse y l’ammontare della popolazione alla generazione
successiva. La parabola blu indica la relazione tra queste due popolazioni
[l’equazione logistica (3)]. Come ci si aspetta, per bassi valori della
popolazione corrente — a sinistra del picco della parabola — la generazione
successiva cresce, mentre il contrario accade a destra del picco. La retta
diagonale a 45º ci aiuta a capire come evolve una popolazione a partire da un
valore iniziale S0. Ad esempio, partendo da un basso valore di S0,
la linea a gradini rossa mostra come la popolazione cambia, generazione dopo
generazione. Il valore della popolazione alla generazione successiva a quella
iniziale (S1) è dato dal punto in cui la linea verticale rossa che
parte da S0 incontra la parabola. Questo valore rappresenta ora il
punto di partenza (sull’asse x) per determinare l’entità della popolazione S2
alla successiva generazione. Per ottenere S2 si estende
orizzontalmente la linea rossa fino ad incontrare la diagonale [dal momento
che lungo questa linea y = x, questa intersezione semplicemente trasforma y
(la popolazione appena determinata) in x (la popolazione corrente da cui
vogliamo ricavare quella successiva)], e poi si prosegue verticalmente fino
ad incontrare di nuovo la parabola. Ripetendo questo procedimento numerose
volte (ovvero con un processo di iterazione), si può ricavare
l’andamento della popolazione al succedersi delle generazioni. Le
figg. 3a,b mostrano un caso in cui,
indipendentemente dal valore di partenza piccolo (S0) o grande (L0),
la popolazione finale si stabilizza su un valore comune (S3=L3).
Se però si aumenta il valore di k, le cose cambiano. Aumentare k significa
rendere la parabola più stretta e spostare il suo picco alla sinistra della
diagonale (geometricamente k rappresenta la tangente alla parabola
nell’origine, ovvero l’inclinazione della linea sottile mostrata nella
figura). Nel caso particolare mostrato in fig. 3c, la popolazione non
acquisisce mai un valore definitivo, ma oscilla stabilmente tra due valori
ben precisi. Un ulteriore aumento di k (fig. 3d) porta al caos: la
soluzione salta da un valore ad un altro (anche molto diverso) in modo
imprevedibile.
Dunque,
una semplice regola iterativa può portare alla stabilità, a oscillazioni,
oppure al caos, a seconda del valore del parametro
k, detto parametro d’ordine. Tutto questo viene
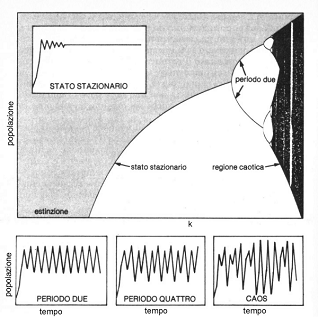
riassunto nel cosiddetto diagramma di biforcazione illustrato in fig.
4. L’asse x del diagramma rappresenta i valori di k. La curva mostra il
comportamento di una popolazione per ogni valore di k. Per bassi valori di quest’ultimo
la popolazione assume un singolo valore ben definito (che aumenta
all’aumentare di k). Al di là di k=3 la curva si biforca in due rami, e la
soluzione oscilla nel tempo tra questi due valori. Un ulteriore aumento di k
porta ad ulteriori biforcazioni: per k=3,5, ad esempio, la popolazione
oscilla regolarmente tra quattro valori definiti. Per valori ancora maggiori
di k il diagramma si confonde in un numero elevato di punti visitati dalla
soluzione con una sequenza essenzialmente imprevedibile. Questa è la regione
caotica. Si noti che ciò che avviene su larga scala (un ramo che si biforca
in due, e poi in quattro, ecc.) lo si ritrova anche
a scale minori (come si nota in fig. 5, che mostra ingrandimenti successivi
di una regione del diagramma principale in fig. 4). Per quanto piccola sia la regione considerata, al suo interno si ritrovano
sempre le stesse strutture presenti su scala maggiore. Oggetti geometrici di
questo genere — in cui una parte, per quanto piccola, è simile al tutto — vengono detti frattali, e ce ne occuperemo nel
prossimo numero.
|