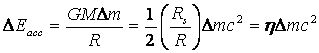|
|
|
|
|
|
|
|
|
Quasar e accrescimento su buchi neri
Annibale D'Ercole
Osservatorio
Astronomico - Bologna
|
L’accrescimento
gravitazionale su oggetti compatti risulta essere di gran lunga il processo fisico
più efficiente per la produzione di energia ed è invocato dagli astrofisici
per spiegare l’emissione di sorgenti ad alta energia sia su scala stellare
(come le binarie X), sia su scala galattica (come i quasar). Supponiamo
che un oggetto di massa M e raggio
R si trovi al centro di una nube
di gas. Anche se inizialmente la nube è ferma, ogni suo singolo elemento
comincerà a cadere radialmente sotto l’azione
gravitazionale del corpo centrale. L’energia cinetica acquisita durante la
caduta viene trasformata in calore quando il gas
urta contro la superficie del corpo centrale e si arresta. Il gas, così
scaldato, emette energia sotto forma di radiazione, raffreddandosi. Per la
conservazione dell’energia, la radiazione emessa è pari al lavoro compiuto
dalla gravità per spostare il gas da una grande distanza fino alla
superficie. Questo lavoro, com’è noto, è pari all’energia potenziale
calcolata al raggio R, e quindi
l’energia irradiata a seguito del processo di accrescimento è pari a
dove G è la costante gravitazionale, c è la velocità della luce e Δm la massa di gas caduta. La formula
è stata riscritta in termini del raggio di Schwarzschild
Rs=2GM/c2, una lunghezza
caratteristica che si associa agli oggetti gravitanti. L’ultima espressione
nell’equazione precedente è particolarmente interessante perché esprime
l’energia irradiata in termini di energia di riposo Δmc2 della massa caduta. Il
parametro
rappresenta
l’efficienza di conversione di questa energia in radiazione. Vale la pena ricordare che la fusione
nucleare tra protoni e neutroni che avviene al centro del Sole, e che porta
alla conversione di idrogeno in elio ed alla produzione di radiazione,
possiede un’efficienza pari allo 0,7% della energia a riposo dei protoni e
dei neutroni; in altre parole η=0,007.
Nei fenomeni di accrescimento l’efficienza dipende da quanto è compatto
l’oggetto centrale. Per una nana bianca, per cui M=M¤ (M¤=2´1033
g è la massa del sole) e R ≈
Se
l’accrescimento avviene in un intervallo di tempo Δt, allora il tasso di accrescimento, ovvero la quantità di gas
che cade nell’unità di tempo, è dato da
In base
alla definizione di efficienza data più sopra, sembrerebbe che valori ancora
maggiori di η possano
ottenersi nel caso in cui l’oggetto centrale sia un buco nero. Il buco nero,
infatti, è l’oggetto più compatto che si possa
immaginare, dal momento che le sue “dimensioni” (l’espressione, ancorché
efficace, è alquanto imprecisa) sono inferiori al raggio di Schwarzschild. Le cose, tuttavia, sono più complesse. Una
volta che un’ipotetica astronave supera il raggio di Schwarzschild,
essa non può più tornare indietro, indipendentemente dalla potenza dei suoi
motori; al di là del raggio di Schwarzschild tutto viene inghiottito dal buco nero e scompare alla vista,
giacché neanche la luce è in grado di uscire. In assenza di una superficie
“solida” contro cui sbattere e riscaldarsi, il gas
in caduta diretta verso un buco nero sembra dunque destinato a scomparire con
la sua energia cinetica senza avere modo di irraggiare. C’è
tuttavia un particolare che fino ad ora abbiamo trascurato. In pratica, il
gas della nube che avvolge inizialmente l’oggetto centrale è dotato di una
qualche rotazione. Anche se inizialmente la velocità di rotazione è molto bassa, man mano che la nube si contrae, la rotazione
aumenta a causa della conservazione del momento angolare (il prodotto r × υr rimane
costante, dove r è la distanza dal
centro di un elemento di gas e υr
la sua velocità di rotazione). Ne consegue che in vicinanza del centro il
gas, a causa della rotazione, non accresce sul buco nero sfericamente da ogni
direzione, ma forma un disco di accrescimento e si avvicina al centro spiraleggiando. Man mano che si addensa in un volume
sempre minore, il gas si comprime e diventa sempre più caldo emettendo
radiazione. Al momento di sparire al di là del raggio di Schwarzschild,
un elemento di fluido avrà trasformato la sua energia potenziale dapprima in
calore e poi in radiazione. Tuttavia,
per un calcolo accurato dell’efficienza η
dobbiamo considerare due dettagli. Il primo è che un oggetto che spiraleggia trasforma solo metà della sua energia
potenziale in energia cinetica di caduta (e conseguentemente in calore e
infine in radiazione), mentre l’altra metà è trasformata in energia cinetica
di rotazione che, in presenza di un buco nero, viene
persa assieme al gas al di là del raggio di Schwarzschild
(per un’orbita circolare la dimostrazione di questa ripartizione energetica è
alquanto semplice e, come si dice in questi casi, viene lasciata come utile
esercizio per il lettore). Nel caso di un disco di accrescimento si ha
dunque:
Il secondo
dettaglio è un effetto tipicamente relativistico. Nonostante che il “punto di
non ritorno” per un oggetto in caduta verso un buco nero sia dato
effettivamente da Rs,
l’ultima orbita stabile per un oggetto che spiraleggia
ha un raggio pari a 3Rs.
A questa distanza la gravità prevale in maniera drammatica e il materiale
raggiunge Rs
in caduta libera, impiegando appena 10-4 s, e dunque non avendo
modo di irraggiare granché prima di scomparire al di là del raggio di Schwarzschild. Sostituendo dunque 3Rs al posto di R nell’equazione (1) e tenendo conto
dell’equazione (2) si ottiene per un buco nero η = 0,08. Dunque, nonostante la sua compattezza, un buco
nero ha un’efficienza simile a quella di una stella di neutroni. Tuttavia,
i buchi neri hanno particolare importanza per due motivi. Innanzitutto,
l’efficienza appena calcolata vale per un buco nero statico; ma un buco nero
in rotazione produce orbite stabili a distanze inferiori a 3Rs e l’efficienza
può arrivare a η = 0,43.
Inoltre, contrariamente alle stelle di neutroni, possono esistere buchi neri
con masse pari a milioni di volte quella del Sole e dunque in grado di
accrescere grandi quantità di materia e irraggiare luminosità enormi. Si
ritiene che la sorgente energetica dei quasar consista proprio
nell’accrescimento su simili buchi neri. Il motivo è dato dalle luminosità di
questi oggetti, pari a centinaia di volte quella della nostra Galassia. Per
ottenere una luminosità tipica di 1047 erg/s, un “motore” basato
sulle reazioni nucleari, con un efficienza di η = 0,007, dovrebbe accrescere
più di |