|
|
|
|
|
|
|
|
|
La fionda gravitazionale
Annibale D'Ercole
Osservatorio
Astronomico - Bologna
|
Una pallina da ping-pong che urta ortogonalmente
con velocità υ’ contro un muro, rimbalza indietro con velocità uguale
e contraria. È facile capire che, se la stessa pallina urta invece contro una
palla da basket che si sta muovendo verso di lei con velocità V’,
rimbalzerà con una velocità superiore a υ’. Le velocità υ e V della
pallina e della palla da basket dopo l’urto possono essere calcolate nel modo
seguente. Assumiamo che le due palle si scontrino
frontalmente in maniera completamente elastica; questo significa che non solo
la quantità di moto, ma anche l’energia cinetica del sistema viene
conservata. Dunque, la somma delle quantità di moto delle due palle deve
rimanere la stessa prima e dopo l’urto e lo stesso vale per la somma delle
energie cinetiche. Possiamo dunque scrivere:
La massa della pallina e quella della
palla da basket sono indicate rispettivamente da m ed
M. Conveniamo di prendere positive le velocità nella direzione del moto della
palla da basket: questo spiega il segno meno presente nell’equazione (1).
Assumiamo per il momento che prima dell’urto il pallone e la pallina abbiano lo stesso valore (a parte il segno) e sia dunque V’=
– υ’ = υo. Questa ipotesi serve solo per
semplificare i calcoli, e verrà abbandonata tra breve. Risolvendo il sistema di
equazioni (1)-(2) si ottiene
dove x = m/M rappresenta il rapporto tra
la massa della pallina e quella della palla da basket. Dal momento che
quest’ultima è molto più pesante, x è molto piccolo e può essere trascurato
nelle equazioni (3) e (4). In definitiva, otteniamo V ≈ υo e υ ≈ 3
υo. Dunque, la palla da basket non si
accorge quasi dell’urto e continua a muoversi sostanzialmente con la stessa
velocità. Al contrario, la pallina triplica la propria velocità e la sua
energia cinetica diventa nove volte maggiore. Da
dove viene questa energia? Naturalmente, è fornita dalla palla da basket
nonostante essa mantenga essenzialmente la velocità iniziale. In effetti,
dall’equazione (3) si vede che l’energia ceduta dalla palla da basket
rappresenta solo una percentuale di 8x della propria energia iniziale –
davvero molto piccola – ma ben l’800% dell’energia iniziale della pallina. Possiamo ora generalizzare il
risultato precedente abbandonando l’ipotesi che le due palle abbiano inizialmente la stessa velocità (a parte il
segno). Il ragionamento è alquanto semplice e vale nel caso in cui x sia
molto piccolo e, dunque, la palla da basket si muova sempre con la stessa
velocità: V = V’.
Poniamoci nel sistema di riferimento
della palla da basket (immaginiamo di “sederci” su di essa);
in questo riferimento quest’ultima è ovviamente ferma, e “vede” la pallina da
ping-pong avvicinarsi con velocità V’ + υ’ prima dell’urto, ed allontanarsi con
la stessa velocità (ma col segno opposto) successivamente. Torniamo ora nel
riferimento iniziale, in cui la palla da basket si muove con velocità V’;
dopo l’urto vedremo muoversi la pallina ad una velocità υ = 2V’ + υ’, dal
momento che la velocità relativa υ – V tra i due oggetti deve
continuare ad essere V’ +
υ’ (come abbiamo dedotto ponendoci nel sistema di
riferimento precedente). È facile verificare che, nel caso in cui
inizialmente le due palle abbiano la stessa velocità, dopo l’urto
la pallina triplica la propria velocità: esattamente il risultato ottenuto in
precedenza. Possiamo ora applicare questi
ragionamenti ad un caso di interesse astronomico. Consideriamo dapprima
l’eventualità molto particolare di una sonda lanciata dalla Terra verso un
pianeta su un’orbita tale per cui essa si avvicina
frontalmente a velocità υ’, mentre il pianeta stesso le va
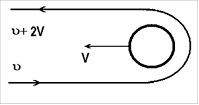
incontro a velocità V. La sonda opererà un’inversione ad “U”, come illustrato
nella figura 2. Si tratta di un caso simile a quello
della pallina da ping-pong che rimbalza contro la palla da basket, anche se
in questo caso il “rimbalzo” non è dovuto a cause
meccaniche ma alla gravità del pianeta; anche in questo caso, tuttavia,
valgono sia la conservazione della quantità di moto che dell’energia e
valgono, quindi, le considerazioni fatte più sopra. Ne consegue che la sonda,
dopo aver interagito con il pianeta, si allontanerà da esso
con una velocità υ = υ’ + 2V, ben più alta di quella
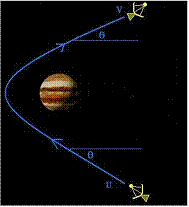
iniziale. La figura 3 illustra il caso, più
realistico, di un’orbita di una sonda la cui orbita viene
deflessa dall’incontro con un pianeta.
Naturalmente, i ragionamenti
precedenti sono validi anche in questo caso, ma bisogna fare attenzione a non
considerare tutta la velocità della sonda, ma solo la componente parallela
alla velocità del pianeta. La figura 3a illustra la situazione nel sistema di
riferimento del pianeta, in cui quest’ultimo è fermo e la sonda alla fine si
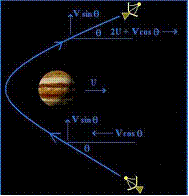
allontana con la stessa velocità con cui si è avvicinata. La figura 3b mostra il fenomeno nel sistema di riferimento del Sole,
in cui la sonda si allontana con una velocità maggiorata di una quantità che
dipende dalla velocità del pianeta e dall’angolo formato da quest’ultima con
la velocità di avvicinamento della sonda. Se i pianeti fossero puntiformi, la
sonda potrebbe guadagnare molta energia ad ogni incontro, passando
vicinissima ad essi, e potrebbe raggiungere una
velocità infinita dopo un numero di incontri finito. In realtà, questo non è
possibile perché i pianeti sono oggetti estesi e perché in un passaggio
troppo ravvicinato la sonda attraverserebbe la loro atmosfera e rallenterebbe
per attrito. |