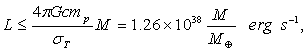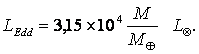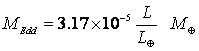|
|
|
|
|
|
|
|
|
Il “limite di Eddington”
Annibale D'Ercole
Osservatorio
Astronomico - Bologna
|
La pressione esercitata su un oggetto
è definita come la forza che agisce sull’unità di superficie (p.e. 1 cm2)
su cui è applicata. La forza, a sua volta, è misurata in base alla variazione
di quantità di moto nell’unità di tempo (p.e. 1 sec.) che produce
sull’oggetto stesso, come stabilito dalla seconda legge di Newton. In
conclusione, la pressione esercitata dal vento sulla vela di una barca è pari
alla quantità di moto comunicata alla vela dagli atomi del vento che
colpiscono 1 cm2 di vela in 1 secondo. Dal momento che, al pari
degli atomi in movimento, i fotoni che compongono la radiazione sono
anch’essi dotati di quantità di moto, un “vento” di radiazione che illumina
un oggetto esercita una pressione sull’oggetto stesso. Nella vita quotidiana
questa pressione è trascurabile, ma in astrofisica può capitare che diventi
molto importante. Vale dunque la pena calcolare la pressione di radiazione. È noto
dagli esperimenti che un singolo fotone trasporta una quantità di moto q =
E/c, dove c è la velocità del fotone (ovvero la velocità della
luce) e E = hν è
l’energia del fotone, pari al prodotto della costante di Plank,
h, per la frequenza del fotone ν (un’espressione alquanto
simile vale per la quantità di moto q = mυ di un oggetto
materiale di massa m e velocità υ una volta che sia
espressa in termini della sua energia cinetica E = ½mυ2:
q = 2E/υ). Supponiamo ora di
avere una sorgente centrale, ad esempio una stella, la cui radiazione si espanda sfericamente dal centro: la pressione che la
radiazione è in grado di esercitare su un’ipotetica superficie sferica di
raggio r concentrica alla stella è data dalla quantità di moto dei
fotoni che colpiscono la superficie ogni secondo. Il numero N di fotoni che in ogni istante
raggiungono la nostra ipotetica superficie sferica è uguale al numero di
fotoni prodotti a ogni istante dalla sorgente centrale. Questi fotoni, moltiplicati
ognuno per la propria energia E,
danno luogo alla luminosità L della
sorgente, definita come l’energia emessa in un secondo: L = NE. Ne consegue che N
= L/E e che la quantità di moto trasportata attraverso la superficie è
pari a Q = Nq
= NE/c = L/c; la pressione di radiazione è data dal flusso della quantità
di moto per unità di superficie, Prad
= Q/4πr2, ovvero
La formula
appena trovata non fornisce ancora l’effettiva forza che la radiazione è in
grado di esercitare su, poniamo, una nube di gas che si trovasse a distanza r da una sorgente di luminosità L. Infatti, se la nube fosse perfettamente trasparente ai
fotoni, questi ultimi non avrebbero modo di interagire con essa. L’opacità di
un gas dipende dalle sue condizioni fisiche; spesso è ragionevole assumere
che il gas sia ionizzato, ovvero che gli elettroni siano slegati dai protoni
(assumiamo per semplicità che il gas sia costituito da idrogeno che è in effetti l’elemento di gran lunga più abbondante) e che
il gas sia composto di fatto da un “mare” di elettroni che compenetra un
“mare” di protoni. In questo caso, l’opacità del gas è
dovuta essenzialmente agli elettroni in quanto reagiscono alla
radiazione molto più prontamente dei protoni che sono quasi 2000 volte più
pesanti. Sono dunque gli elettroni che vengono
soffiati via dal “vento” di radiazione; i protoni, però, rimangono
“agganciati” agli elettroni tramite la forza elettrostatica e vengono
trascinati via anch’essi. In conclusione, la forza effettiva Frad esercitata dalla radiazione su un
singolo elettrone è una frazione sT del valore calcolato più sopra, dove
sT è la
cosiddetta “sezione d’urto Thompson” che tiene
conto dell’opacità degli elettroni: Sulla nube
agisce anche la gravità, in particolare sui protoni che sono più pesanti. Per
un singolo protone vale:
dove mp è la massa del protone ed M la massa della sorgente centrale.
Dunque, un protone tende a cadere verso il centro a causa di Fgrav e ad allontanarsi a grandi raggi
a causa di Frad. Perché del
materiale possa cadere sull’oggetto centrale è necessario che la forza
esercitata dalla radiazione non superi quella gravitazionale (Frad £ Fgrav). Questa condizione può essere
riscritta come una condizione sulla luminosità, e si ottiene:
dove M¤=2´1033
g indica la massa del Sole. Questa disuguaglianza è nota come «limite di Eddington» e stabilisce che un oggetto centrale di data
massa non può avere una luminosità superiore alla «luminosità di Eddington» data (in unità di luminosità solari L¤=4´1033
erg s-1) da:
Alternativamente,
possiamo dire che, per realizzare una determinata luminosità, è richiesta una
massa centrale minima detta «massa di Eddington»
che, espressa in masse solari, è data da:
Il limite
di Eddington trova una naturale applicazione nel
campo dell’astrofisica delle alte energie e, in particolare, nello studio dei
quasar, galassie nel cui centro viene prodotta
tipicamente una luminosità L=1046
erg s-1, cento volte superiore a quella di tutta la nostra
Galassia. Si ritiene che questa radiazione venga
prodotta da gas che, cadendo verso un oggetto centrale, trasforma la sua
energia cinetica prima in calore e poi in radiazione. Per quanto discusso più
sopra, risulta che l’oggetto centrale responsabile dell’elevata luminosità
dei quasar deve avere una massa pari o superiore alla massa di Eddington M =
8´107
M¤. Dal
momento che la luminosità varia su scale temporali di pochi anni, se ne
deduce (si veda il numero precedente delle Spigolature) che le dimensioni
dell’oggetto centrale devono essere inferiori al parsec (1 pc = 3,08´1018
cm). Ne deriva per l’oggetto centrale una densità circa
cento volte superiore a quella che troviamo nel nucleo centrale di
stelle della nostra Galassia. A causa di una densità così elevata, si ritiene
che il “motore” responsabile della luminosità dei quasar sia un buco nero. Il
meccanismo di accrescimento gravitazionale è in grado di produrre radiazione
con un’efficienza dalle 10 alle 60 volte superiore a quella che caratterizza
le reazioni nucleari responsabili della radiazione emessa dalle stelle (si
veda il numero precedente delle Spigolature). A
proposito di stelle, il limite di Eddington ci
indica quale sia la massa massima che una stella può
avere. Le stelle sono sfere di gas in equilibrio idrostatico in cui la
gravità è controbilanciata dalla pressione del gas stesso. Durante la maggior
parte della vita di una stella (la cosiddetta fase di Sequenza Principale)
c’è una relazione tra la massa M
di quest’ultima e la sua luminosità L;
maggiore è la massa, più intense sono le reazioni nucleari e dunque, in
ultima analisi, maggiore è la radiazione prodotta. La proporzionalità tra
massa e luminosità per le stelle più massicce è data da L |