L’equazione del tempo
Claudio Elidoro

Non so se, di fronte a una meridiana, al lettore succeda la stessa cosa, ma a me viene quasi spontaneo guardare subito il mio orologio da polso. Non è che non sappia leggere ciò che mi dice l’orologio solare – benché, talvolta, ci si imbatta in schemi un po’ complicati – ma è quasi un riflesso incondizionato, dettato forse dalla voglia di vedere “quanto preciso” possa essere l’orario descritto dall’ombra sul muro. Ovviamente è molto difficile che le due indicazioni dell’orario siano pienamente concordi, ma la colpa non è certo da ascrivere alla cattiva progettazione e realizzazione della meridiana. Tutt’altro.

Sveliamo subito il colpevole: tutto dipende dal moto della Terra intorno al Sole, un moto che non è affatto così regolare come potremmo pensare. Optando per una visione più geocentrica, potremmo dar la colpa alla non regolarità del movimento del nostro astro diurno sulla volta celeste, ma la sostanza rimarrebbe comunque la stessa. Dopo aver additato il colpevole, però, è necessario soffermarsi ad analizzare, almeno per sommi capi, gli elementi in gioco nell’intera faccenda.

Finché lo scorrere del tempo nelle attività umane è stato scandito unicamente dal ritmico sorgere e tramontare del Sole e dai suoi giochi d’ombra, non si poneva alcun problema. Il mezzogiorno veniva con precisione decretato dalla culminazione del Sole: era cioè l’istante in cui il nostro astro raggiungeva la sua massima altezza in cielo. E poco importava se nella città vicina tale culminazione avvenisse prima o dopo – ancora non c’era motivo di doversi preoccupare della sincronizzazione dei tempi – e men che meno si sentiva l’impellente esigenza di controllare la regolarità del cammino del Sole in cielo. A partire del xvii secolo, però, l’ingegno umano cominciò a ideare meccanismi sempre più precisi per misurare e indicare lo scorrere del tempo e ben presto ci si accorse che il moto diurno del Sole non era affatto regolare (a dire il vero, già i Babilonesi se n’erano accorti e Tolomeo aveva dedicato all’argomento un intero capitolo del suo Almagesto).

La necessità di uniformare per ragioni pratiche – almeno all’interno di uno stesso stato – l’indicazione dell’orario fece sì che dalla metà del xix secolo venisse preferito al tempo solare (cioè quello indicato dalle meridiane) il tempo solare medio indicato dagli orologi[1]. In pratica ci si mise tutti quanti d’accordo e si stabilì che ciascun giorno fosse lungo esattamente 24 ore. Un errore dal punto di vista astronomico, ma certamente un’incredibile comodità nella misurazione dell’orario necessaria per tutte le attività umane. È proprio questa scelta che sta all’origine del disaccordo tra meridiane e orologi cui si accennava all’inizio: rispetto al regolare scorrere dei secondi segnato da un orologio, infatti, il tempo scandito dal Sole non è altrettanto regolare. Questo comporta che i due orologi non indichino lo stesso orario e l’orologio solare si trovi ad essere talvolta in anticipo oppure in ritardo rispetto a quello meccanico o elettronico, una differenza che può anche superare i 16 minuti. Tale differenza, variabile nel corso dell’anno, tra il “tempo solare vero” e il “tempo solare medio” è nota come Equazione del tempo e il suo valore è identico, allo stesso istante, per tutti i luoghi della Terra.

Si diceva che all’origine dell’Equazione del tempo vi è il moto irregolare della Terra intorno al Sole. Molte sono le componenti di tale irregolarità, ma sono in particolare due quelle che interessano la nostra analisi: l’eccentricità dell’orbita terrestre e la sua inclinazione (obliquità dell’eclittica).

Se la Terra orbitasse intorno al Sole percorrendo un cerchio perfetto, la sua velocità sarebbe costante in ogni punto dell’orbita. Ma non è così: l’orbita del nostro pianeta è ellittica e questo comporta che in prossimità del perielio (il punto più vicino al Sole) la velocità della Terra sia più elevata rispetto a quando, sei mesi più tardi, si trova all’afelio (è una situazione che trova la sua descrizione matematica nella seconda legge di Keplero). Visto da un osservatore sulla Terra, dunque, il moto del Sole sulla sfera celeste raggiunge la sua massima velocità intorno ai primi di gennaio (passaggio al perielio) per poi rallentare e toccare la velocità più bassa all’inizio di luglio (afelio). Se si muovesse con velocità costante, la culminazione avverrebbe sempre alla medesima ora, cioè a mezzogiorno in punto. La velocità irregolare, invece, fa sì che, per ritornare al momento della culminazione, la Terra impieghi più tempo (se il suo moto sull’orbita è più rapido) oppure meno tempo (se il moto è più lento), rispetto al giorno medio misurato dagli orologi. Questo comporta che il giorno solare reale risulti un po’ più lungo o un po’ più corto del precedente. Nei giorni a ridosso del passaggio al perielio o all’afelio la differenza tra un giorno e il successivo ammonta a circa 8 secondi. Ovviamente, i ritardi (o gli anticipi) di ciascun giorno si sommano l’uno con l’altro, tanto che intorno ad aprile il Sole è in ritardo di oltre 7 minuti, mentre a ottobre è in anticipo della stessa quantità.

La seconda irregolarità che consideriamo è quella imputabile all’inclinazione esistente tra il piano dell’orbita e l’asse di rotazione terrestre. Questa benefica inclinazione assicura il regolare susseguirsi delle stagioni, ma per chi osserva il moto del Sole in cielo comporta che, nel corso dell’anno, il nostro astro appaia più alto o più basso rispetto all’orizzonte. Il cammino del Sole, in altre parole, non è un moto regolare lungo l’equatore celeste ed ecco che la componente “verticale” del suo spostamento diventa fonte di irregolarità rispetto al movimento costante che sta alla base del tempo indicato dagli orologi. In particolare, i due tempi saranno perfettamente identici in occasione degli equinozi e dei solstizi, ma negli altri giorni il Sole accumulerà fino a quasi 10 minuti di ritardo (o di anticipo) rispetto ai nostri orologi.

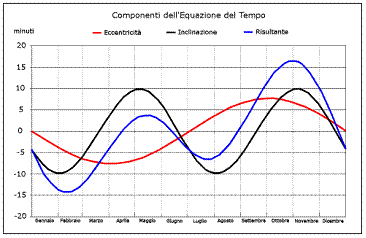
Ovviamente, nel corso dell’anno, queste due irregolarità si sommano tra loro e la situazione può essere riassunta nel grafico mostrato in Fig. 1. Il sommarsi o l’annullarsi delle due irregolarità fa sì che una meridiana si trovi “avanti” di circa 16 minuti e mezzo rispetto agli orologi nei primi giorni di novembre, mentre resterà “indietro” fino a 14 minuti nei giorni intorno a metà febbraio.

I più attenti hanno sicuramente notato che molto spesso le meridiane solari recano proprio un grafico molto simile a quello raffigurato (ovviamente viene riportata soltanto la risultante delle due irregolarità). È un tacito invito, se si vuole valutare l’accuratezza della meridiana nell’indicarci l’ora, a non dimenticarci della pesante componente racchiusa nell’Equazione del tempo.

 

 

Fig. 1. Equazione del tempo. Nel grafico sono riportate le componenti dell’Equazione del tempo dovute all’eccentricità dell’orbita della Terra (linea rossa) e all’inclinazione dell’asse terrestre rispetto al piano dell’orbita (linea nera). Il risultato della loro composizione (linea azzurra) rappresenta l’andamento dell’Equazione del tempo nel corso dell’anno.

 

Home
Spigolature

 

Livello
Avanzato

 


[1] Per chi fosse interessato ad approfondire questi argomenti, può vedere in questa rivista: A. D'Ercole, Storia del Tempo, 1998, n. 3, p. 2; F. Pollastri, Visita guidata alla misura del Tempo, 1998, n. 3, p. 18; T. Aebischer, La correzione del tempo: i secondi bisestili, 2004, n. 3, p. 4.