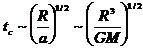|
|
|
|
|
|
|
|
|
Sulla massa delle galassie
Annibale
DErcole
|
Consideriamo una nube
autogravitante in equilibrio, in cui, cioè, la propria forza di gravità sia
bilanciata dalla pressione dovuta allenergia termica del gas. [Per
semplicità trascuriamo la presenza di un alone di material oscura.] Questa
energia termica è data dallenergia cinetica delle particelle che compongono
il gas: maggiore è lenergia cinetica, maggiore è la temperatura. Dalla
meccanica statistica sappiamo che lenergia media di una singola particella
può essere espressa come kT, dove k
è la costante di Boltzmann e T è
la temperatura della nube. Daltra parte, lenergia potenziale di questa
stessa particella, ad esempio un protone, si può scrivere come GMmp/R, dove G è la costante di gravitazione, mp la massa del protone, M la massa della nube (assunta
sferica) ed R il suo raggio. In
una nube in equilibrio si ha pertanto:
[Qui
siamo interessati solo a considerazioni di ordine di grandezza e a mettere in
luce gli aspetti fisici dei meccanismi esposti, piuttosto che le procedure
matematiche necessarie per descriverli (peraltro troppo complesse in questo
ambito). Per questo motivo le costanti numeriche dellordine dellunità vengono
trascurate.] Date
le masse caratteristiche delle nubi protogalattiche, lenergia di ogni
singola particella è assai superiore allenergia necessaria per ionizzare
lidrogeno collisionalmente:
Il
termine a destra della disuguaglianza rappresenta il potenziale di
ionizzazione dellidrogeno, ed è espresso in termini della massa me e della carica q dellelettrone, e della costante di
Plank h. In base a quanto appena
detto possiamo dunque considerare la nube (che per semplicità assumiamo
composta solamente da idrogeno) completamente ionizzata. Come
abbiamo detto nel livello base, una nube autogravitante tende a porsi in
equilibrio. Tuttavia è possibile che questo equilibrio venga spezzato a causa
delle perdite radiative. Perché questo possa avvenire, è necessario che tr £ tc,
ovvero che il tempo di raffreddamento sia inferiore al tempo di collasso,
cioè al tempo impiegato dalla nube ad addensarsi al centro; in questo caso,
infatti, il calore prodotto dalla compressione viene irraggiato rapidamente,
invece di essere incamerato dal gas, e la compressione può procedere
ulteriormente. Per
capire, dunque, sotto quali condizioni sia possibile la formazione di una
galassia, è necessario calcolare esplicitamente i tempi tc e tr.
Calcolo di tr -
La quantità di energia L emessa
nellunità di tempo da un elettrone sottoposto ad un accelerazione a è
data dalla formula di Larmor
dove q è la carica dellelettrone e c è la velocità della luce. Dal
momento che, come abbiamo visto, il gas è ionizzato, gli elettroni si muovono
liberamente tra i protoni. Consideriamo allora un elettrone dotato velocità u che giunge in
prossimità di un protone. Arrivato a una distanza b da questultimo, lelettrone risente della forza attrattiva di
Coulomb che si esercita tra le due particelle, la cui intensità è dellordine
di mea ~ (q2/b2), e
subisce dunque unaccelerazione a ~
(q2/meb2).
La formula di Larmor diventa quindi L ~
(q6/me2c3)(1/b4). Per ottenere Lt , lenergia totale
irraggiata per unità di volume, è necessario tenere conto della densità di
elettroni ne e di
protoni np, e dei
contributi che provengono dalle diverse distanze b. Il calcolo esatto è troppo complesso per poter essere
riportato in queste note; un calcolo approssimato, benché più abbordabile, ci
porterebbe lontano dallargomento di queste spigolature. Ci limitiamo
pertanto a riportare lespressione per Lt
senza ulteriori commenti:
Lirraggiamento
appena descritto, dovuto a un gas caldo ionizzato, è detto radiazione di bremsstrahlung. Il
tempo di raffreddamento è definito come il tempo necessario per irraggiare
tutta lenergia termica. Avendo assunto un gas di puro idrogeno, possiamo
scrivere ni = ne = n; lenergia termica per unità di volume è allora pari a nkT e
il tempo di raffreddamento è dato da
Calcolo di tc -
Consideriamo una nube fredda, ovvero la cui energia termica sia
trascurabile rispetto a quella gravitazionale. In questo caso la nube tenderà
a contrarsi sotto il suo stesso peso senza che la pressione del gas possa
esercitare alcun contrasto. Si dice allora che la nube collassa, e gli
strati più esterni precipitano verso il centro in caduta libera. Comè noto,
nella vita quotidiana un oggetto lasciato cadere liberamente è soggetto ad
unaccelerazione costante g e
percorre, in un tempo t, una
distanza r = 0.5gt2. Ribaltando questa
formula, possiamo dire che il tempo impiegato da un oggetto per cadere in
terra da unaltezza r è pari a t = (2r/g)1/2. Tornando alla nostra nube, un elemento di
gas posto alla sua superficie è sottoposto ad una accelerazione a = GM/R2; questa accelerazione non è costante perché R diminuisce man mano che il collasso
procede. Tuttavia, noi siamo interessati solo a valutazioni di ordini di
grandezza e dunque applichiamo ugualmente la formula per il tempo di caduta
ricavata più sopra. Otteniamo pertanto per il tempo di collasso la seguente
espressione:
Dalla
condizione tr < tc
ricaviamo
Se
ora consideriamo una nube con raggio pari a Rcr e teniamo conto delle equazioni (1) e (2),
otteniamo finalmente la seguente condizione:
Questo
risultato indica che una nube con massa ~ 1011 M
e raggio ~ 70 kpc può raffreddare rapidamente e formare strutture legate
gravitazionalmente. Durante questa fase la nube si contrae fino a un raggio
dellordine di 10-20 kpc, tipico delle galassie più grandi. Quello appena
descritto rappresenta dunque un possibile scenario per la formazione delle
galassie, dal momento che molte galassie hanno una massa dellordine di Mcr. Si noti che Mcr e Rcr derivano unicamente dalle costanti fondamentali
della fisica. |