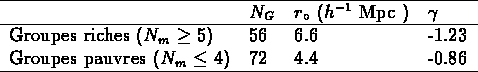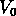Différences entre groupes CfA et SSRS

La question maintenant est de savoir si les NGs et les SGs peuvent être considerés comme deux échantillons dérivés de la même distribution, ou si la distribution réelle ou les paramètres de l'algorithme utilisé pour les identifier sont à l'origine de cette différence.

• RGH90 suggèrent par exemple qu'une partie de la différence pourrait être due à l'utilisation de valeurs différentes du paramètre pour sélectionner les groupes (350 km/s pour les NGs contre 600 km/s pour les SGs). Un paramètre 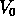trop grand serait la cause d'une plus grande proportion de galaxies apparement dans un groupe qui en réalité n'en sont pas membres ( interlopers). Je ne crois pas que ce soit l'explication correcte, car cet effet n'est pas très grand par rapport au contraste de densité.

• Il y a aussi une différence dans le contraste choisi pour la recherche (plus grand pour les NGs, 80 contre 20 pour les SGs). Le catalogue de groupes Sud a une fraction plus élevée de groupes pauvres résultant probablement du contraste inférieur utilisé pour la sélection. Une fraction significative de ces groupes est fausse (RGH89 ont remarqué qu'au moins un tiers des groupes avec 3 ou 4 membres identifiés par l'algorithme dans le catalogue CfA ne sont pas réels; et 37% des NGs et 57% des SGs ont seulement 3 membres). Ce fait peut avoir deux conséquences. L'une est que les faux groupes seront moins correlés; l'autre est que les groupes pauvres auront une corrélation plus faible que les groupes riches si la relation richesse des systèmes -- amplitude de leur corrélation est vérifiée. Cela pourrait expliquer pourquoi les groupes sont plus correlés dans l'hémisphère nord que dans le sud.

  Pour vérifier cette explication, j'ai donc calculé 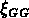pour deux sous-échantillons de NG2, l'un avec les 72 groupes qui ont un nombre de membres 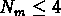, l'autre avec les 56 groupes qui ont 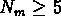. Les résultats, qui sont très bruités, montrent que les groupes riches ont une longueur de corrélation plus grande (6.6 contre 4.4) que les groupes pauvres. La fraction supérieure de groupes pauvres semble aplatir la pente de 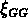et en réduire l'amplitude. Entre 6 et 7 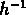Mpc la fonction de corrélation 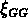de tous les sous-échantillons NG montre un maximum secondaire, tandis que entre 7 et 8 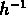Mpc la 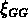de tous les sous-échantillons SG montre un minimum secondaire, ce qui rend plus plate la 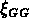nord et plus raide la 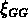sud.

• Une autre explication possible est la nature même des deux catalogues (voir la discussion dans le troisième chapitre de cette thèse): l'un est limité en magnitude et dominé par le riche amas de Coma, l'autre est limité en diamètre et a une tendance à sélectionner de manière privilegiée les galaxies spirales. On a vu dans le chapitre précèdent que cette différence de critère de sélection provoque des répercussions aux niveau des statistiques d'ordre supérieur en ce qui concerne les galaxies. On a vu par exemple que des différences réelles existent au niveau des percolations et des vides. On peut alors penser à un comportement analogue pour les groupes de galaxies . Dans le catalogue CfA on devrait trouver avec une probabilité supérieure des groupes plus riches et plus corrélés: c'est ce que l'on observe.

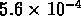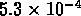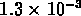• Les échantillons NG1 et NG2 ont des densités respectivement de et , tandis que les échantillons SG1 et SG2 ont des densités respectivement de et 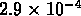, approximativement deux fois plus grandes. Des différences significatives dans l'estimation de la fonction de corrélation peuvent être generées suivant si l'on utilise, comme densité de normalisation, le nombre d'objets divisé par le volume total de l'échantillon, comme dans le cas des groupes, ou si l'on calcule l'intégrale de la fonction de luminosité (Blanchard et Alimi, 1988). En effet il est impossible de déterminer une vraie densité moyenne des groupes dans les petits échantillons actuellement disponibles. Pourtant cet effet devrait diminuer l'amplitude de la 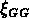des groupes CfA, et ne peut donc pas expliquer la différence observée.

  
Table: Paramètres de la fonction de corrélation des groupes CfA ``riches" et ``pauvres"