Oke & Korycansky (1982), studying a sample of high redshift QSOs,
defined two depression factors, ![]() and
and ![]() ,
characterizing the amount of absorption between Ly
,
characterizing the amount of absorption between Ly![]() and Ly
and Ly![]() and between Ly
and between Ly![]() and the Lyman limit respectively:
and the Lyman limit respectively: ![]() ,
where
,
where ![]() and
and ![]() are the observed and intrinsic fluxes per unit wavelength in the QSO restframe.
are the observed and intrinsic fluxes per unit wavelength in the QSO restframe. ![]() is defined in the same way as
is defined in the same way as![]() .
We adopted the estimates given by Madau (1995) for the attenuation of the
continuum due to line blanketing as a function of redshift. He found the
flux decrements averaged over all the lines of sight to be
.
We adopted the estimates given by Madau (1995) for the attenuation of the
continuum due to line blanketing as a function of redshift. He found the
flux decrements averaged over all the lines of sight to be
![$\displaystyle 1 - \frac{1}{\Delta \lambda_A}\int_{1050(1+z_{\rm em})}^{1170(1+......ac{\lambda_{\rm obs}}{\lambda_\alpha}\right)^{3.46}\right]\,d\lambda_{\rm obs}$](img139.gif) |
(2) | ||
![$\displaystyle 1 - \frac{1}{\Delta \lambda_B}\int_{920(1+z_{\rm em})}^{1015(1+z......{\lambda_{\rm obs}}{\lambda_j}\right)^{3.46} \right] \,d\lambda_{\rm obs} \: ,$](img142.gif) |
(3) |
where ![]() Å
and
Å
and ![]() Å.
The coefficient
Å.
The coefficient ![]() relative to the Ly
relative to the Ly![]() forest contribution is equal to
forest contribution is equal to ![]() .
The main contribution to
.
The main contribution to ![]() ,
representing the flux decrement caused by all Lyman series lines, belongs
to Ly
,
representing the flux decrement caused by all Lyman series lines, belongs
to Ly![]() ,
Ly
,
Ly![]() (
(![]() Å)
and Ly
Å)
and Ly![]() (
(![]() Å),
whose coefficients are
Å),
whose coefficients are ![]() ,
, ![]() and
and ![]() .
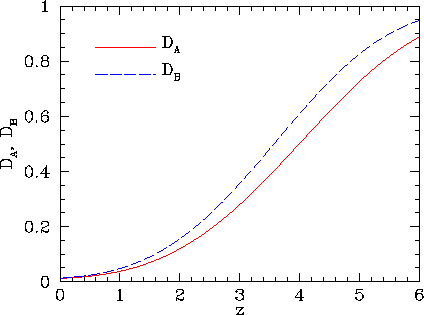
Figure 5 shows the depression factors
.
Figure 5 shows the depression factors ![]() and
and ![]() as computed from equations 2 and 3.
The fact that
as computed from equations 2 and 3.
The fact that![]() implies that Ly
implies that Ly![]() and higher order lines contribute significantly to line blanketing. We
have applied Madau's prescriptions to compute the opacity of IGM through
the mean factors
and higher order lines contribute significantly to line blanketing. We
have applied Madau's prescriptions to compute the opacity of IGM through
the mean factors ![]() and
and ![]() ,
whereas we approximated the Lyman continuum absorption setting
,
whereas we approximated the Lyman continuum absorption setting ![]() for both observed and synthetic SEDs below
for both observed and synthetic SEDs below ![]() ,
where
,
where ![]() Å
is the Lyman limit.
Å
is the Lyman limit.
 |