Initial Mass Function
The IMF 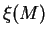 specifies the distribution in mass of a newly formed stellar population
and it is frequently assumed to be a simple power law:
specifies the distribution in mass of a newly formed stellar population
and it is frequently assumed to be a simple power law: 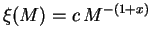 .
In general,
.
In general, 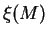 is assumed to extend from a lower to an upper cutoff, chosen to be
is assumed to extend from a lower to an upper cutoff, chosen to be 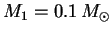 and
and 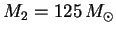 in GISSEL. In Table 1 we show the parameters
of the three most used IMFs: the Salpeter (1955), Scalo (1986) and Miller
& Scalo (1979) laws, in the form used by Bruzual & Charlot in their
evolutionary synthesis model.
in GISSEL. In Table 1 we show the parameters
of the three most used IMFs: the Salpeter (1955), Scalo (1986) and Miller
& Scalo (1979) laws, in the form used by Bruzual & Charlot in their
evolutionary synthesis model.
Table:Parameters of Salpeter (1955), Scalo
(1986) and Miller & Scalo (1979) laws for the IMF: 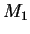 and
and 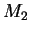 are the lower and higher mass cutoffs, and
are the lower and higher mass cutoffs, and 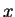 is the parameter of the power law.
is the parameter of the power law.
| IMF |
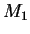 |
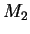 |
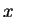 |
| Salpeter |
0.10 |
125. |
1.35 |
| Scalo |
0.10 |
0.18 |
-2.60 |
| |
0.18 |
0.42 |
0.01 |
| |
0.42 |
0.62 |
1.75 |
| |
0.62 |
1.18 |
1.08 |
| |
1.18 |
3.50 |
2.50 |
| |
3.50 |
125. |
1.63 |
| Miller & Scalo |
0.10 |
1.00 |
0.25 |
| |
1.00 |
2.00 |
1.00 |
| |
2.00 |
10.0 |
1.30 |
| |
10.0 |
125. |
2.30 |
|
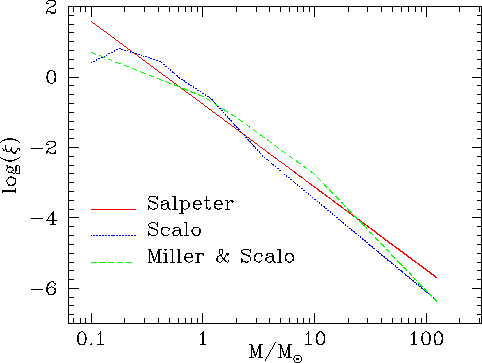 |
Figure:The three IMFs used
in the spectral evolutionary models of Bruzual & Charlot (1993).
The different slopes of the three considered laws produce different spectral
energy distributions: the Scalo and Miller & Scalo laws are flat at
small masses and less rich of massive stars with respect to the Salpeter
law, as illustrated in Figure 2. The large
number of massive stars in the Salpeter law produces an excess of UV flux,
whereas the Scalo law generates too many solar mass stars, making the spectrum
too red to match the observed colours.
We adopted the Miller & Scalo law as a good compromise. We also
tested the influence of a change in IMF, finding a negligible effect in
photometric redshift computation (Bolzonella et al. 2000).
micol bolzonella
2000-12-10
