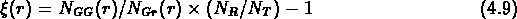
J'ai recalculé la fonction de corrélation en utilisant différents sous-échantillons, avec l'estimateur standard décrit dans le deuxième chapitre:
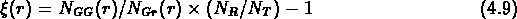
où 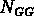 est cette fois le nombre de paires de groupes qui ont
une séparation r.
J'ai utilisé 50 catalogues aléatoires avec un nombre
d'objets égal au nombre d'objets observés,
et j'ai estimé les erreurs
poissoniennes et dites de ``bootstrap" pour
est cette fois le nombre de paires de groupes qui ont
une séparation r.
J'ai utilisé 50 catalogues aléatoires avec un nombre
d'objets égal au nombre d'objets observés,
et j'ai estimé les erreurs
poissoniennes et dites de ``bootstrap" pour 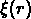 .
J'ai utilisé trois méthodes pour tenir compte de la
sélection des objets en fonction du décalage vers le rouge:
le fit de la distribution en densité,
la fonction de sélection dérivée
de la fonction de luminosité (pour le catalogue CfA),
et l'attribution des décalages vers le rouge
observés aux objets aléatoires avec un lissage pour
éliminer les traces des structures aux petites échelles.
.
J'ai utilisé trois méthodes pour tenir compte de la
sélection des objets en fonction du décalage vers le rouge:
le fit de la distribution en densité,
la fonction de sélection dérivée
de la fonction de luminosité (pour le catalogue CfA),
et l'attribution des décalages vers le rouge
observés aux objets aléatoires avec un lissage pour
éliminer les traces des structures aux petites échelles.
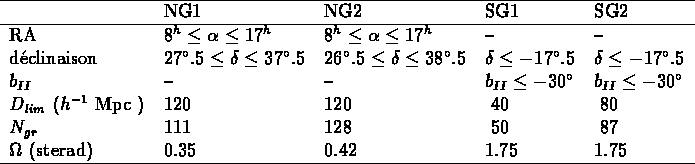
Table: Paramètres des sous-échantillons des groupes
CfA et SSRS
Pour tester s'il existait des effets systématiques de volume et s'assurer de
la stabilité des résultats, j'ai calculé la fonction de corrélation
des groupes dans deux échantillons CfA, NG1 et NG2,
et deux échantillons SSRS, SG1 et SG2, que je vais définir
(leurs limites sont résumées dans la table ![]() ):
):
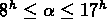 ,
, 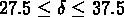 ,
, 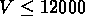 km/s;
km/s;
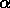 ,
,
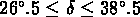 ,
, 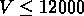 km/s;
km/s;
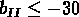 ,
, 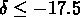 ,
,
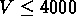 km/s;
km/s;
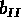 et
et 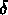 ,
,
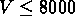 km/s.
km/s.
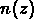 .
.
Ces résultats confirment que la longueur de corrélation 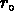 des
groupes de l'hémisphère sud est la moitié de celle des groupes nord,
et que ces derniers ont une fonction de corrélation
des
groupes de l'hémisphère sud est la moitié de celle des groupes nord,
et que ces derniers ont une fonction de corrélation 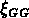 de
pente moins raide.
de
pente moins raide.
Pour les échantillons de l'hémisphère nord, nous pouvons
estimer la fonction de sélection par d'autres moyens.
La densité des groupes est une fonction du
redshift, avec des sommets qui correspondent aux grandes structures,
et suit à peu près le comportement de la densité des
galaxies CfA, comme cela a été établi par RGH90;
on peut donc prendre la même fonction de sélection que
pour les galaxies,
estimée à partir de la fonction de luminosité avec les paramètres
donnés par de Lapparent et al. (1988), c'est à dire une
fonction de Schechter avec 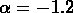 et
et
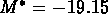 . Dans ce cas, on trouve pour l'échantillon NG1
. Dans ce cas, on trouve pour l'échantillon NG1
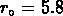 et
et 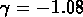 .
Si l'on utilise pour l'échantillon aléatoire les
décalages vers le rouge des objets observés,
et un lissage gaussien avec
.
Si l'on utilise pour l'échantillon aléatoire les
décalages vers le rouge des objets observés,
et un lissage gaussien avec 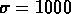 km/s,
on trouve
km/s,
on trouve 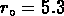
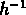 Mpc et
Mpc et 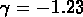 ;
si l'on choisit
;
si l'on choisit 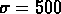 km/s, les résultats ne changent pas en
manière significative (
km/s, les résultats ne changent pas en
manière significative (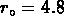 ,
, 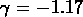 ).
).
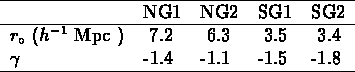
Table: Paramètres de la fonction de corrélation des groupes
Ces résultats sont en accord avec ceux trouvés par
RGH90 (ils donnent 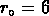 et une pente
et une pente 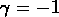 ,
avec la même fonction de sélection des galaxies), et
ils estiment leurs incertitudes à peu près à 2.5
,
avec la même fonction de sélection des galaxies), et
ils estiment leurs incertitudes à peu près à 2.5 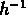 Mpc pour
Mpc pour 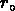 et
à 50% pour la pente, valeurs comparables aux nôtres.
et
à 50% pour la pente, valeurs comparables aux nôtres.
Pour avoir une idée des incertitudes, il faut
souligner les différences d'amplitude et de pente
entre NG1 et NG2, qui diffèrent simplement de 17 groupes.
Donc la fonction de corrélation 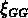 des groupes NG
semble avoir une pente moins raide
que celle des galaxies (
des groupes NG
semble avoir une pente moins raide
que celle des galaxies (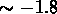 ), mais l'erreur est assez grande
pour ne pas permettre d'exclure cette valeur.
), mais l'erreur est assez grande
pour ne pas permettre d'exclure cette valeur.
Pour SG1, en utilisant une fonction de sélection estimée
à partir de la relation observée densité-décalage vers le
rouge, et en l'appliquant
au catalogue aléatoire, comme pour les groupes NGs, avec le fit entre
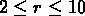
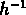 Mpc on a
Mpc on a 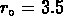 et
et 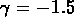 .
.
Pour SG2 le fit entre 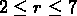
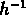 Mpc
donne
Mpc
donne 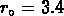 ,
, 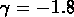 .
Comme pour l'échantillon total nord, j'ai aussi utilisé les
décalages vers le rouge
observés pour les catalogues aléatoires, avec
.
Comme pour l'échantillon total nord, j'ai aussi utilisé les
décalages vers le rouge
observés pour les catalogues aléatoires, avec 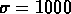 km/s:
le fit entre
km/s:
le fit entre 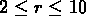
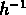 Mpc donne
Mpc donne 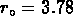
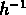 Mpc et
Mpc et
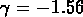 .
.
Nos résultats sont en accord avec ceux de Maia et da Costa (1990; MDC) qui trouvent une amplitude 2.5 fois inférieure à celle des galaxies.
La figure ![]() montre la
montre la 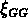 de NG2 et SG2.
de NG2 et SG2.
Les différentes méthodes donnent des résultats comparables:
il faut conclure que les groupes CfA et SSRS
ont des fonctions de corrélation significativement
différentes:
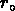 vaut entre 5 et 6
vaut entre 5 et 6 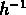 Mpc pour les NGs, entre 3 et 4
Mpc pour les NGs, entre 3 et 4 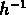 Mpc pour les SGs.
Mpc pour les SGs.

Figure: Fonction de corrélation des groupes identifiés dans les
catalogues CfA et SSRS