



Next: Groupes classiques et
Up: Groupes de galaxies
Previous: Conclusions
Le contraste ne modifie pas seulement les caractéristiques de la distribution
des groupes: il donne également des résultats différents au niveau
de certaines quantités physiques que l'on détermine, comme la dimension,
la dispersion de vitesse, la masse ou
le crossing time. Comme l'ont remarqué MDL, la distribution des
valeurs de chaque variable peut différer d'un catalogue à l'autre,
mais la valeur médiane de chaque quantité est comparable
à contraste égal.
L'algorithme d'Huchra & Geller est basé sur
le principe de maintenir le contraste constant à tous les décalages
vers le rouge, et cherche à compenser le fait que le catalogue perd
de plus en plus de galaxies avec la profondeur.
Evidemment, il ne compense pas le fait que nous observons une partie
différente de la fonction de luminosité des galaxies à chaque
valeur de la profondeur.
La probabilité qu'un groupe pauvre ait au moins 3 galaxies de
luminosité supérieure à une luminosité 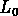 donnée
est inférieure à celle que présente un groupe riche; ainsi
beaucoup de groupes pauvres ne peuvent pas être detectés par
l'algorithme à très grandes distances
même en augmentant le rayon de recherche et/ou la vitesse.
A priori, on s'attend à ce que
les groupes qui sont de préférence détectés aux
grandes distances sont ceux qui possèdent des galaxies lumineuses,
et qui sont riches et étendus; ces groupes seront au contraire
sous-représentés aux petites distances à cause du petit volume
échantilloné et du scaling de R.
donnée
est inférieure à celle que présente un groupe riche; ainsi
beaucoup de groupes pauvres ne peuvent pas être detectés par
l'algorithme à très grandes distances
même en augmentant le rayon de recherche et/ou la vitesse.
A priori, on s'attend à ce que
les groupes qui sont de préférence détectés aux
grandes distances sont ceux qui possèdent des galaxies lumineuses,
et qui sont riches et étendus; ces groupes seront au contraire
sous-représentés aux petites distances à cause du petit volume
échantilloné et du scaling de R.
De plus, la richesse apparente peut différer sensiblement de la richesse
réelle: si la fonction de sélection vaut par exemple 0.1
(c'est à dire qu'on détecte 10% des galaxies à cette distance)
il est évident que la plus grande fraction de groupes avec 3 membres
apparents sera donnée par les groupes avec 30 membres réels,
mais avec une dispersion sensible, le tout mélangé par les
contributions des groupes de diverses richesses
(il est facile de calculer qu'un groupe avec 10 membres sera détecté
comme un groupe de 3 membres dans 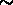 6% des cas). La présence d'un
effet richesse -- amplitude de
6% des cas). La présence d'un
effet richesse -- amplitude de 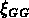 rend difficile
l'interprétation de l'analyse statistique.
rend difficile
l'interprétation de l'analyse statistique.
Le paramètre le plus significatif qui a un biais sensible avec
la distance est le rayon projeté des groupes, montré en fig.  .
.

Figure: Séparation projetée moyenne 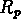 des groupes en fonction du
redshift
des groupes en fonction du
redshift
Il est clair, quand on observe la fig.  ,
que la valeur moyenne de
,
que la valeur moyenne de 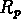 à un redshift donné est
similaire (légèrement inférieure) à la valeur de
à un redshift donné est
similaire (légèrement inférieure) à la valeur de
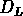 au même redshift, et les deux quantités suivent
approximativement le même comportement.
Nous sommes en train de sélectionner les groupes
dont le rayon
au même redshift, et les deux quantités suivent
approximativement le même comportement.
Nous sommes en train de sélectionner les groupes
dont le rayon 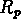 est proche de
est proche de 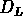 ;
donc l'histogramme des fréquences de
;
donc l'histogramme des fréquences de 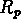 peut être conditionné
par cet effet, et ne représente pas la vraie distribution des
peut être conditionné
par cet effet, et ne représente pas la vraie distribution des 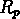 .
.
Pour éviter donc ce genre de problèmes, et pour obtenir une
distribution de paramètres significative, il faut
échantilloner la même partie de la fonction de luminosité
à toutes les distances, avec le même contraste.
Cela implique qu'il faut utiliser des catalogues de galaxies
limités en volumes.
Le catalogues actuels ne sont pas assez grands pour permettre
une statistique significative, mais je vais montrer comment
un catalogue limité en volume simplifie l'analyse.
J'ai appliqué l'algorithme de Huchra & Geller
à différents échantillons limités en volume
extraits de la tranche de 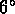 du catalogue CfA2
(qui représent à peu près la moitié du catalogue où
RHG89 ont cherché leurs groupes);
le facteur d'échelle R est donc constant dans chaque
sous-échantillon.
du catalogue CfA2
(qui représent à peu près la moitié du catalogue où
RHG89 ont cherché leurs groupes);
le facteur d'échelle R est donc constant dans chaque
sous-échantillon.

Table: Paramètres des 5 échantillons limités en volume
On a défini 5 échantillons limités en volume, avec des vitesses radiales
limites respectives 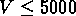 km/s,
km/s, 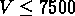 km/s,
km/s,
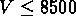 km/s,
km/s, 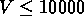 km/s,
km/s, 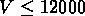 km/s
(voir table
km/s
(voir table  ).
Pour le catalogue GR1, limité à M=-18, on a choisi
).
Pour le catalogue GR1, limité à M=-18, on a choisi
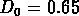
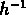 Mpc , qui correspond à un
contraste
Mpc , qui correspond à un
contraste 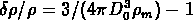 (où
(où
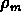 est la densité moyenne du sous-échantillon)
à peu près 80, et
est la densité moyenne du sous-échantillon)
à peu près 80, et 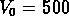 km/s. Pour comparaison,
on rappelle que RGH89 utilisent
km/s. Pour comparaison,
on rappelle que RGH89 utilisent 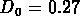
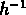 Mpc (qui correspond
lui aussi dans leur cas à un contraste de 80) et
Mpc (qui correspond
lui aussi dans leur cas à un contraste de 80) et 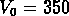 km/s
à la vitesse de réference
km/s
à la vitesse de réference 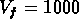 km/s.
km/s.
Dans le cas des autres échantillons, nous avons tenu compte de la
différence en densité, correspondant à l'intégration de parties
différentes de la fonction de luminosité.
La densité varie à peu près d'un ordre de grandeur
de M=-18 à 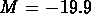 , ainsi le facteur d'échelle
, ainsi le facteur d'échelle
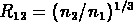 varie un peu plus que d'un facteur 2.
Ceci permet d'avoir même à une distance de 12000 km/s des paramètres
physiquement raisonnables, et de pouvoir comparer des groupes à
diverses distances.
varie un peu plus que d'un facteur 2.
Ceci permet d'avoir même à une distance de 12000 km/s des paramètres
physiquement raisonnables, et de pouvoir comparer des groupes à
diverses distances.
Nous avons trouvé pour les 5 sous-échantillons
respectivement 7, 12, 12, 10 et 6
groupes.
Dans le premier échantillon nous trouvons les
groupes les plus petits, formés par des galaxies relativement
moins lumineuses. Leur dispersion de vitesse typique est de
140 km/s, leur crossing time est en général inférieur à
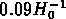 (qui correspond au crossing time pour un groupe virialisé;
voir Nolthenius & White, 1987), et leur masse du viriel
est
(qui correspond au crossing time pour un groupe virialisé;
voir Nolthenius & White, 1987), et leur masse du viriel
est 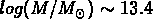 ; dans le dernier sous-échantillon
nous avons les systèmes les plus grands, avec une
dispersion de vitesse élevée,
; dans le dernier sous-échantillon
nous avons les systèmes les plus grands, avec une
dispersion de vitesse élevée,
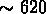 km/s, des crossing times au dessous du limite
de virialisation (à une exception, un groupe qui possède aussi
une dispersion de vitesse particulièrement basse),
et des masses entre
km/s, des crossing times au dessous du limite
de virialisation (à une exception, un groupe qui possède aussi
une dispersion de vitesse particulièrement basse),
et des masses entre 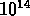 et
et 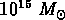 ; il est évident qu'ici
on a à faire à une classe ``d'amas"
où nous retrouvons Coma, detecté dans tous les autres sous-échantillons
excepté naturellement le premier.
En plus, dans GR2 et GR3, Coma apparaît divisé en deux
groupes proches.
Au contraire, les groupes nord 56 et 57 ont été detecté
comme un seul groupe, à une position qui correspond à un groupe
compact d'Hickson.
; il est évident qu'ici
on a à faire à une classe ``d'amas"
où nous retrouvons Coma, detecté dans tous les autres sous-échantillons
excepté naturellement le premier.
En plus, dans GR2 et GR3, Coma apparaît divisé en deux
groupes proches.
Au contraire, les groupes nord 56 et 57 ont été detecté
comme un seul groupe, à une position qui correspond à un groupe
compact d'Hickson.
Finalement, nous avons constitué un catalogue final de 30 groupes de vitesses
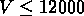 km/s, sélectionnant les groupes de vitesses
km/s, sélectionnant les groupes de vitesses
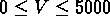 km/s dans GR1,
km/s dans GR1, 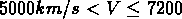 km/s dans GR2,
km/s dans GR2,
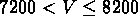 km/s
dans GR3,
km/s
dans GR3, 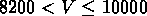 km/s dans GR4 et
km/s dans GR4 et
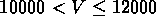 km/s dans GR5 (voir table
km/s dans GR5 (voir table  ).
Les limites en vitesse sont plus ou moins arbitraires
et un choix différent ne change pas significativement
le catalogue de groupes.
).
Les limites en vitesse sont plus ou moins arbitraires
et un choix différent ne change pas significativement
le catalogue de groupes.
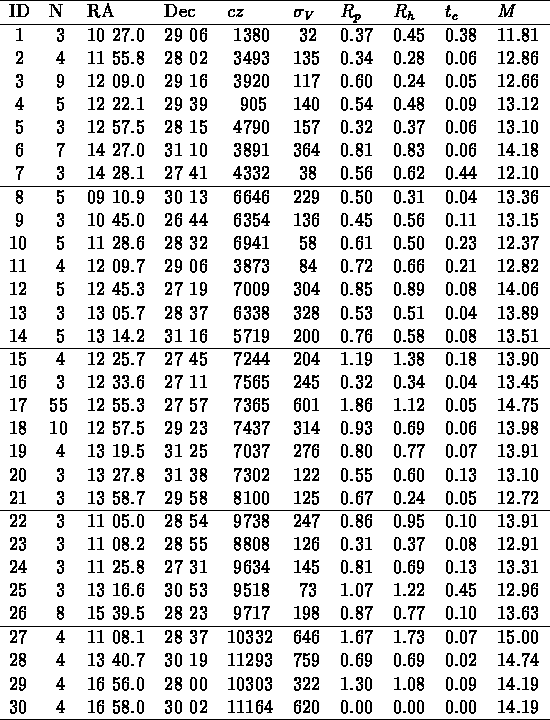
Table: Liste des groupes trouvé dans 5 échantillons
limités en volume; contraste = 80
Nous avons identifié 19 NGs qui correspondent à nos groupes, et
tous ont au moins 5 membres. RGH89 trouvent
32 groupes avec 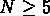 et
et 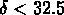 . Nous n'avons pas retrouvé
les groupes riches qui ont une trop grande dispersion de vitesse et
ceux composés de galaxies proches et intrinséquement faibles,
mais nous avons aussi identifié 11 nouveaux groupes.
. Nous n'avons pas retrouvé
les groupes riches qui ont une trop grande dispersion de vitesse et
ceux composés de galaxies proches et intrinséquement faibles,
mais nous avons aussi identifié 11 nouveaux groupes.

Figure: 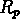 des groupes selectionnés dans 5 échantillons limités
en volume
des groupes selectionnés dans 5 échantillons limités
en volume
La fig. nous donne
nous donne 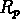 pour ce catalogue et
pour ce catalogue et 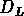 pour
chacun des 5 sous-échantillons. Ici à nouveau, nous avons le même
comportement qu'auparavant: les échantillons les plus profonds recensent
les groupes les plus grands.
Mais maintenant les types de groupes sont plus clairement identifiables
et ne sont pas mélangés comme dans le cas d'un catalogue limité
en magnitude apparente.
pour
chacun des 5 sous-échantillons. Ici à nouveau, nous avons le même
comportement qu'auparavant: les échantillons les plus profonds recensent
les groupes les plus grands.
Mais maintenant les types de groupes sont plus clairement identifiables
et ne sont pas mélangés comme dans le cas d'un catalogue limité
en magnitude apparente.
La fig. montre que l'on peut
définir trois classes principales de groupes sur la base de leur
montre que l'on peut
définir trois classes principales de groupes sur la base de leur 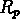 :
:
- une première classe de petits groupes,
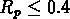 , où nous trouvons
5 groupes visibles seulement dessous de cz = 9000 km/s dans notre
catalogue;
, où nous trouvons
5 groupes visibles seulement dessous de cz = 9000 km/s dans notre
catalogue;
- une deuxième classe de groupes de dimension moyenne,
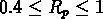 ,
où se trouve la majorité des groupes,
visibles dans tout l'intervalle des distances à partir de
v = 3000 km/s jusqu'à 12000 km/s;
,
où se trouve la majorité des groupes,
visibles dans tout l'intervalle des distances à partir de
v = 3000 km/s jusqu'à 12000 km/s;
- finalement, une troisième classe de groupes de grande dimension
(amas),
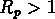 , où nous retrouvons 5 autres groupes
au delà de cz = 7000 km/s.
, où nous retrouvons 5 autres groupes
au delà de cz = 7000 km/s.
Les conclusions sont donc les suivantes.
-
L'algorithme utilisé pour sélectionner les groupes dans les catalogues
de galaxies limités en magnitude (ou diamètre)
sélectionne et mélange des types différents de groupes
en fonction de la distance.
- La signification physique de
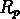 est douteuse, étant donnée sa dépendance en fonction
du décalage vers le rouge et en particulier sa corrélation avec
le rayon de recherche.
est douteuse, étant donnée sa dépendance en fonction
du décalage vers le rouge et en particulier sa corrélation avec
le rayon de recherche.
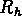 aussi a un comportement similaire, mais moins prononcé,
comme l'ont montré RGH90.
aussi a un comportement similaire, mais moins prononcé,
comme l'ont montré RGH90.
- Finalement, je souligne l'importance de pouvoir disposer
de catalogues de groupes définis à partir d'un catalogue
de galaxies limité en volume, en magnitude
absolue, parce que cela nous permet d'utiliser des paramètres fixes,
et de minimiser les biais induits par la distance.
Il faut aussi ajouter que, si l'on s'intéresse à la comparaison
relative des groupes observés dans des régions différentes du ciel
ou résultant de simulation numériques, le problème est moins grave,
mais il est important d'avoir des catalogues construits suivant
des critères de sélection comparables.




Next: Groupes classiques et
Up: Groupes de galaxies
Previous: Conclusions
alberto cappi
Wed Feb 5 10:43:08 MET 1997
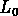 donnée
est inférieure à celle que présente un groupe riche; ainsi
beaucoup de groupes pauvres ne peuvent pas être detectés par
l'algorithme à très grandes distances
même en augmentant le rayon de recherche et/ou la vitesse.
A priori, on s'attend à ce que
les groupes qui sont de préférence détectés aux
grandes distances sont ceux qui possèdent des galaxies lumineuses,
et qui sont riches et étendus; ces groupes seront au contraire
sous-représentés aux petites distances à cause du petit volume
échantilloné et du scaling de R.
donnée
est inférieure à celle que présente un groupe riche; ainsi
beaucoup de groupes pauvres ne peuvent pas être detectés par
l'algorithme à très grandes distances
même en augmentant le rayon de recherche et/ou la vitesse.
A priori, on s'attend à ce que
les groupes qui sont de préférence détectés aux
grandes distances sont ceux qui possèdent des galaxies lumineuses,
et qui sont riches et étendus; ces groupes seront au contraire
sous-représentés aux petites distances à cause du petit volume
échantilloné et du scaling de R.
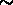 6% des cas). La présence d'un
effet richesse -- amplitude de
6% des cas). La présence d'un
effet richesse -- amplitude de 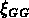 rend difficile
l'interprétation de l'analyse statistique.
rend difficile
l'interprétation de l'analyse statistique.

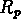 des groupes en fonction du
redshift
des groupes en fonction du
redshift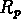 à un redshift donné est
similaire (légèrement inférieure) à la valeur de
à un redshift donné est
similaire (légèrement inférieure) à la valeur de
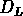 au même redshift, et les deux quantités suivent
approximativement le même comportement.
Nous sommes en train de sélectionner les groupes
dont le rayon
au même redshift, et les deux quantités suivent
approximativement le même comportement.
Nous sommes en train de sélectionner les groupes
dont le rayon 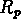 est proche de
est proche de 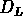 ;
donc l'histogramme des fréquences de
;
donc l'histogramme des fréquences de 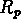 peut être conditionné
par cet effet, et ne représente pas la vraie distribution des
peut être conditionné
par cet effet, et ne représente pas la vraie distribution des 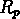 .
.
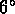 du catalogue CfA2
(qui représent à peu près la moitié du catalogue où
RHG89 ont cherché leurs groupes);
le facteur d'échelle R est donc constant dans chaque
sous-échantillon.
du catalogue CfA2
(qui représent à peu près la moitié du catalogue où
RHG89 ont cherché leurs groupes);
le facteur d'échelle R est donc constant dans chaque
sous-échantillon.

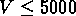 km/s,
km/s, 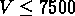 km/s,
km/s,
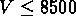 km/s,
km/s, 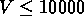 km/s,
km/s, 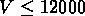 km/s
(voir table
km/s
(voir table 
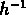 Mpc , qui correspond à un
contraste
Mpc , qui correspond à un
contraste 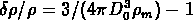 (où
(où
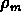 est la densité moyenne du sous-échantillon)
à peu près 80, et
est la densité moyenne du sous-échantillon)
à peu près 80, et 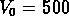 km/s. Pour comparaison,
on rappelle que RGH89 utilisent
km/s. Pour comparaison,
on rappelle que RGH89 utilisent 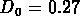
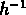 Mpc (qui correspond
lui aussi dans leur cas à un contraste de 80) et
Mpc (qui correspond
lui aussi dans leur cas à un contraste de 80) et 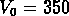 km/s
à la vitesse de réference
km/s
à la vitesse de réference 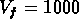 km/s.
km/s.
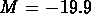 , ainsi le facteur d'échelle
, ainsi le facteur d'échelle
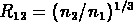 varie un peu plus que d'un facteur 2.
Ceci permet d'avoir même à une distance de 12000 km/s des paramètres
physiquement raisonnables, et de pouvoir comparer des groupes à
diverses distances.
varie un peu plus que d'un facteur 2.
Ceci permet d'avoir même à une distance de 12000 km/s des paramètres
physiquement raisonnables, et de pouvoir comparer des groupes à
diverses distances.
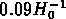 (qui correspond au crossing time pour un groupe virialisé;
voir Nolthenius & White, 1987), et leur masse du viriel
est
(qui correspond au crossing time pour un groupe virialisé;
voir Nolthenius & White, 1987), et leur masse du viriel
est 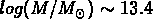 ; dans le dernier sous-échantillon
nous avons les systèmes les plus grands, avec une
dispersion de vitesse élevée,
; dans le dernier sous-échantillon
nous avons les systèmes les plus grands, avec une
dispersion de vitesse élevée,
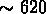 km/s, des crossing times au dessous du limite
de virialisation (à une exception, un groupe qui possède aussi
une dispersion de vitesse particulièrement basse),
et des masses entre
km/s, des crossing times au dessous du limite
de virialisation (à une exception, un groupe qui possède aussi
une dispersion de vitesse particulièrement basse),
et des masses entre 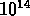 et
et 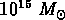 ; il est évident qu'ici
on a à faire à une classe ``d'amas"
où nous retrouvons Coma, detecté dans tous les autres sous-échantillons
excepté naturellement le premier.
En plus, dans GR2 et GR3, Coma apparaît divisé en deux
groupes proches.
Au contraire, les groupes nord 56 et 57 ont été detecté
comme un seul groupe, à une position qui correspond à un groupe
compact d'Hickson.
; il est évident qu'ici
on a à faire à une classe ``d'amas"
où nous retrouvons Coma, detecté dans tous les autres sous-échantillons
excepté naturellement le premier.
En plus, dans GR2 et GR3, Coma apparaît divisé en deux
groupes proches.
Au contraire, les groupes nord 56 et 57 ont été detecté
comme un seul groupe, à une position qui correspond à un groupe
compact d'Hickson.
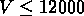 km/s, sélectionnant les groupes de vitesses
km/s, sélectionnant les groupes de vitesses
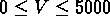 km/s dans GR1,
km/s dans GR1, 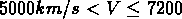 km/s dans GR2,
km/s dans GR2,
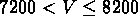 km/s
dans GR3,
km/s
dans GR3, 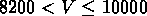 km/s dans GR4 et
km/s dans GR4 et
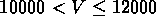 km/s dans GR5 (voir table
km/s dans GR5 (voir table 
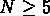 et
et 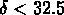 . Nous n'avons pas retrouvé
les groupes riches qui ont une trop grande dispersion de vitesse et
ceux composés de galaxies proches et intrinséquement faibles,
mais nous avons aussi identifié 11 nouveaux groupes.
. Nous n'avons pas retrouvé
les groupes riches qui ont une trop grande dispersion de vitesse et
ceux composés de galaxies proches et intrinséquement faibles,
mais nous avons aussi identifié 11 nouveaux groupes.

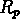 des groupes selectionnés dans 5 échantillons limités
en volume
des groupes selectionnés dans 5 échantillons limités
en volume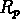 pour ce catalogue et
pour ce catalogue et 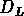 pour
chacun des 5 sous-échantillons. Ici à nouveau, nous avons le même
comportement qu'auparavant: les échantillons les plus profonds recensent
les groupes les plus grands.
Mais maintenant les types de groupes sont plus clairement identifiables
et ne sont pas mélangés comme dans le cas d'un catalogue limité
en magnitude apparente.
pour
chacun des 5 sous-échantillons. Ici à nouveau, nous avons le même
comportement qu'auparavant: les échantillons les plus profonds recensent
les groupes les plus grands.
Mais maintenant les types de groupes sont plus clairement identifiables
et ne sont pas mélangés comme dans le cas d'un catalogue limité
en magnitude apparente.
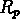 :
:
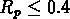 , où nous trouvons
5 groupes visibles seulement dessous de cz = 9000 km/s dans notre
catalogue;
, où nous trouvons
5 groupes visibles seulement dessous de cz = 9000 km/s dans notre
catalogue;
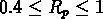 ,
où se trouve la majorité des groupes,
visibles dans tout l'intervalle des distances à partir de
v = 3000 km/s jusqu'à 12000 km/s;
,
où se trouve la majorité des groupes,
visibles dans tout l'intervalle des distances à partir de
v = 3000 km/s jusqu'à 12000 km/s;
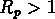 , où nous retrouvons 5 autres groupes
au delà de cz = 7000 km/s.
, où nous retrouvons 5 autres groupes
au delà de cz = 7000 km/s.
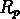 est douteuse, étant donnée sa dépendance en fonction
du décalage vers le rouge et en particulier sa corrélation avec
le rayon de recherche.
est douteuse, étant donnée sa dépendance en fonction
du décalage vers le rouge et en particulier sa corrélation avec
le rayon de recherche.
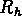 aussi a un comportement similaire, mais moins prononcé,
comme l'ont montré RGH90.
aussi a un comportement similaire, mais moins prononcé,
comme l'ont montré RGH90.