
Figure: Effet Binggeli (Binggeli, 1982).
 est l'angle formé par
le grand axe projeté d'un amas d'Abell et la ligne qui connecte son
centre au centre de l'amas le plus proche. D est la distance qui sépare
les deux amas.
est l'angle formé par
le grand axe projeté d'un amas d'Abell et la ligne qui connecte son
centre au centre de l'amas le plus proche. D est la distance qui sépare
les deux amas.
West, Dekel et Oemler (1987; 1989) ont réalisé des simulations numériques de formation d'amas dans différents scénarios théoriques. Le but de leur travail était d'étudier les propriétés des amas résultant de simulations, pour identifier les caractéristiques qui gardent un ``souvenir" des conditions initiales. Ils ont déduit de leur étude que les profils de densité et de dispersion de vitesse ne diffèrent pas significativement suivant le modèle; le degré de subclustering est difficile à définir (à quel point peut-on parler de sous-amas ou définir des amas séparés?), mais ils n'ont pas détecté un degré significatif de sous-structure; au contraire, le degré d'alignement des amas, et la relation masse -- rayon semblent être des caractéristiques qui discriminent fortement les scénarios de formation. Leur pas successif a été de confronter ces caractéristiques sur des données observationnelles.
Par exemple, il semble que les grands axes des amas présentent une tendance à s'orienter dans la direction de l'amas le plus proche (effet ``Binggeli").

Figure: Effet Binggeli (Binggeli, 1982).  est l'angle formé par
le grand axe projeté d'un amas d'Abell et la ligne qui connecte son
centre au centre de l'amas le plus proche. D est la distance qui sépare
les deux amas.
est l'angle formé par
le grand axe projeté d'un amas d'Abell et la ligne qui connecte son
centre au centre de l'amas le plus proche. D est la distance qui sépare
les deux amas.
L'effet est clair sur
la fig.![]() , publiée par Binggeli (1982), qui
montre l'angle
, publiée par Binggeli (1982), qui
montre l'angle  formé par le grand axe projeté d'un amas
d'Abell et la ligne qui connecte son centre au centre de l'amas
le plus proche, et D est la distance qui sépare les deux amas.
Ils trouvent que cet effet est difficilement explicable dans le cadre d'un
Univers de CDM .
formé par le grand axe projeté d'un amas
d'Abell et la ligne qui connecte son centre au centre de l'amas
le plus proche, et D est la distance qui sépare les deux amas.
Ils trouvent que cet effet est difficilement explicable dans le cadre d'un
Univers de CDM .
West et al. (1987) trouvent aussi que les profils de masse des amas résultant des simulations sont en bon accord avec les profils observés d'un échantillon d'amas qui sera défini ensuite: ce fait semble suggérer que dans les amas la lumière suit la masse. Ces profils suivent bien une loi de de Vaucouleurs:
où 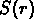 est le profil de densité et
est le profil de densité et 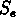 est la densité de surface
au rayon
est la densité de surface
au rayon 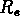 .
Si l'on intègre le profil (
.
Si l'on intègre le profil (![]() ) sur tous les rayons, on obtient
la masse totale:
) sur tous les rayons, on obtient
la masse totale:
Ils montrent que 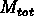 est une quantité bien définie, qui
n'est pas très sensible à l'extrapolation du profil aux grands
rayons, où il est mal connu, pourvu que ce profil converge rapidement,
comme le profil de de Vaucouleurs (même s'il ne devient jamais nul).
est une quantité bien définie, qui
n'est pas très sensible à l'extrapolation du profil aux grands
rayons, où il est mal connu, pourvu que ce profil converge rapidement,
comme le profil de de Vaucouleurs (même s'il ne devient jamais nul).
Etant donné que, dans un univers d'Einstein-de Sitter, et dans le cadre
de l'approximation linéaire, la densité interne
moyenne suit la relation 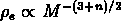 , et si l'on prend
, et si l'on prend
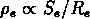 , on peut déduire de l'équation (
, on peut déduire de l'équation (![]() )
la relation suivante entre masse et rayon:
)
la relation suivante entre masse et rayon:
où

Non seulement les simulations confirment la relation
(![]() ), mais aussi
les observations, qui donnent
), mais aussi
les observations, qui donnent 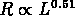 ,
(ce qui est plus favorable
à un univers hiérarchique avec n = 0).
,
(ce qui est plus favorable
à un univers hiérarchique avec n = 0).
Mais quelles sont les caractéristiques de leur échantillon d'amas? Ayant pour but l'analyse d'un échantillon homogène, West et al. ont reanalysé la photométrie de ces amas, et ils ont calculé les profils utilisant la loi de de Vaucouleurs. Ils en ont déduit la luminosité totale, en utilisant la fonction de luminosité de Schechter (1976) avec les paramètres de Kirshner et al. (1983), et en extrapolant à un rayon infini.
Ils arrivent à
la conclusion que les erreurs aléatoires sur la luminosité de
l'amas peuvent être chiffrées à 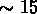 %; ils constatent aussi que
les erreurs systématiques peuvent être plus grandes, mais
qu'elles ne peuvent
pas avoir d'effet sur la pente de la relation R - L à laquelle
ils s'intéressent.
%; ils constatent aussi que
les erreurs systématiques peuvent être plus grandes, mais
qu'elles ne peuvent
pas avoir d'effet sur la pente de la relation R - L à laquelle
ils s'intéressent.
Ils notent que le rayon d'Abell 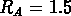
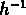 Mpc est pratiquement le double
du rayon qui contient la moitié de la lumière, ce qui signifie que
la luminosité dans un rayon d'Abell est une bonne approximation,
à un facteur 2 près, de la luminosité totale de l'amas; la limite
dans la procédure d'Abell est donc surtout une limite en luminosité totale,
et non en brillance de surface, qui aurait pu engendrer une relation
entre L et R du type observé.
Mpc est pratiquement le double
du rayon qui contient la moitié de la lumière, ce qui signifie que
la luminosité dans un rayon d'Abell est une bonne approximation,
à un facteur 2 près, de la luminosité totale de l'amas; la limite
dans la procédure d'Abell est donc surtout une limite en luminosité totale,
et non en brillance de surface, qui aurait pu engendrer une relation
entre L et R du type observé.
Ils donnent pour chaque amas le rapport
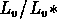 (luminosités totales dans la bande visuelle,
extrapolées à un rayon infini; voir aussi Oemler, 1974), avec
(luminosités totales dans la bande visuelle,
extrapolées à un rayon infini; voir aussi Oemler, 1974), avec
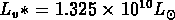 .
.
Grâce donc à ce travail de West, Dekel et Oemler, nous avons pu utiliser leur mesures des rayons et des luminosités de 29 amas (West et al., 1989, qui remarquent: with a few exceptions, these represent all clusters with with reliable determinations of both the cluster profile and luminosity function).
Le troisième paramètre qui nous intéresse est la dispersion de vitesse que nous avons puisée dans des données ultérieures. Parmi ces 29 amas, 16 ont des dispersions de vitesse mesurées qui sont disponibles dans la compilation de Struble & Rood (1991). Ces dispersions de vitesse ont été mesurées avec un nombre de galaxies supérieur à 50 pour 12 amas, et entre 13 et 20 pour les 4 autres. Il s'agit donc de mesures assez fiables. En outre, on peut les considérer comme des dispersions centrales, car on observe en général les régions centrales, les plus concentrées, d'un amas, pour maximiser la probabilité que les galaxies observées soient des membres réels de l'amas.
Comme West et al. nous avons choisi 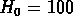 km/s Mpc
km/s Mpc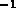 et
et 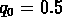 .
.