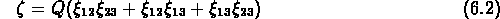
On a vu que les amas ont une fonction de corrélation de pente comparable à celle des galaxies. De plus, Tóth, Hollósi & Szalay (1989) et Jing et Zhang (1989) ont montré que leur fonction de corrélation à trois points peut être décomposée en somme de produits de fonctions de corrélation à deux points comme pour les galaxies:
avec une constante 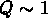 , comparable elle aussi à la valeur
déterminée pour les galaxies.
Szapudi, Szalay & Boschán (1992) ont récemment
confirmé la validité de la hiérarchie pour les galaxies jusqu'à N=8,
utilisant le catalogue du Lick, et confirment l'amplification
de la corrélation à deux points des amas relativement aux galaxies
et la validité de la relation (
, comparable elle aussi à la valeur
déterminée pour les galaxies.
Szapudi, Szalay & Boschán (1992) ont récemment
confirmé la validité de la hiérarchie pour les galaxies jusqu'à N=8,
utilisant le catalogue du Lick, et confirment l'amplification
de la corrélation à deux points des amas relativement aux galaxies
et la validité de la relation (![]() ) pour les amas.
) pour les amas.
Pour les galaxies une loi d'invariance d'échelle
a été observée pour les probabilités de vides, comme prévu par
les modèles hiérarchiques: la probabilité de vides normalisée,
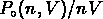 , dépend seulement de
, dépend seulement de 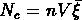 ,
où
,
où 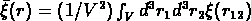 .
Il est naturel de se demander
si les amas montrent aussi cette propriété, et si la loi d'échelle
est la même que celle des galaxies.
.
Il est naturel de se demander
si les amas montrent aussi cette propriété, et si la loi d'échelle
est la même que celle des galaxies.
En collaboration avec S. Maurogordato et M. Lachièze-Rey,
j'ai analysé différents échantillons d'amas extraits du
catalogue de Tully (1987b). Les probabilités de vides ont été calculées
avec des sphères de rayon R (avec typiquement entre 10000 et 100000
sphères pour chaque rayon consideré)
placées aléatoirement dans le catalogue,
et comptant les sphères qui ne contiennent pas d'amas.
Quant à 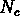 , nous l'avons calculé directement à partir de
l'integrale
, nous l'avons calculé directement à partir de
l'integrale 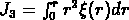 .
Si
.
Si 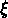 suit une loi de puissance, on peut montrer que:
suit une loi de puissance, on peut montrer que:
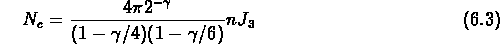
ce qui donne la relation approchée 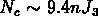 pour
pour
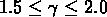 .
.
Le comportement des probabilités de vides des amas
est très similaire à celui
des galaxies. Le catalogue limité à 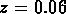 s'écarte des autres.
Cela n'est pas très surprenant, car ce catalogue enserre exactement
le vide du Bouvier.
Au contraire, l'échantillon le plus grand, limité à
s'écarte des autres.
Cela n'est pas très surprenant, car ce catalogue enserre exactement
le vide du Bouvier.
Au contraire, l'échantillon le plus grand, limité à
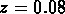 , suit bien la courbe qui représente les galaxies.
Quand on a publié notre article (Cappi, Maurogordato & Lachièze-Rey, 1991,
qui se trouve en appendice), on estimait le catalogue complet à
80% jusqu'à
, suit bien la courbe qui représente les galaxies.
Quand on a publié notre article (Cappi, Maurogordato & Lachièze-Rey, 1991,
qui se trouve en appendice), on estimait le catalogue complet à
80% jusqu'à 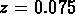 . Les données successives de Postman et al.
(1992) nous ont permis de compléter l'échantillon et
de confirmer le résultat.
. Les données successives de Postman et al.
(1992) nous ont permis de compléter l'échantillon et
de confirmer le résultat.
La figure ![]() montre la probabilité de vides
de différents échantillons d'amas de galaxies, avec la courbe
qui définit la loi trouvée pour les galaxies CfA.
montre la probabilité de vides
de différents échantillons d'amas de galaxies, avec la courbe
qui définit la loi trouvée pour les galaxies CfA.

Figure: 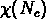 en fonction de
en fonction de 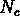 pour un échantillon d'amas
à
pour un échantillon d'amas
à  et
et 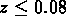 .
.
En perspective, les comptages pourraient nous offrir des
informations complémentaires. Le problème réside toujours
dans la faible densité des catalogues d'amas et la taille limitée des
échantillons à notre disposition.
Pour les comptages, nous avons utilisé les données de la
Deep Abell Redshift Survey (Huchra et al., 1990; HHPG).
Le catalogue HHPG couvre une région du ciel de 561 degrés carrés,
avec 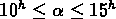 et
et 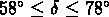 ,
pour un total de 145 amas d'Abell avec
,
pour un total de 145 amas d'Abell avec 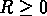 et
et  .
Leur décalage vers le rouge moyen est de 0.16.
La figure
.
Leur décalage vers le rouge moyen est de 0.16.
La figure ![]() montre les
montre les 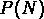 en fonction de N
pour des rayons compris entre 5 et 65
en fonction de N
pour des rayons compris entre 5 et 65 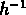 Mpc ; pour chaque rayon on a utilisé
un million de sphères tirées au hasard.
Il est intéressant de remarquer que pour un catalogue poissonien
la pente des
Mpc ; pour chaque rayon on a utilisé
un million de sphères tirées au hasard.
Il est intéressant de remarquer que pour un catalogue poissonien
la pente des 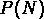 devrait varier continuement en fonction du
rayon. Au contraire, dans notre cas aux rayons intermédiaires
les
devrait varier continuement en fonction du
rayon. Au contraire, dans notre cas aux rayons intermédiaires
les 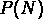 montrent une pente fixe. Selon les modèles à invariance
d'échelle, cette pente doit être égal à
montrent une pente fixe. Selon les modèles à invariance
d'échelle, cette pente doit être égal à 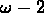 .
Sur la figure la ligne droite a une pente de -1.4, qui correspond
à
.
Sur la figure la ligne droite a une pente de -1.4, qui correspond
à 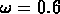 trouvé précedemment dans l'analyse des vides.
Il y a un accord satisfaisant avec les données.
trouvé précedemment dans l'analyse des vides.
Il y a un accord satisfaisant avec les données.
On a dejà défini, dans le deuxième chapitre, les échelles
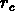 et
et 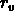 . Nous savons que le modèles d'invariance d'échelle
prevoient, pour des valeurs très grandes de
. Nous savons que le modèles d'invariance d'échelle
prevoient, pour des valeurs très grandes de 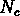 ,
,
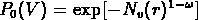 , où
, où 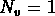 quand
quand
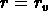 . Si l'on prend l'HHPG coupé à
. Si l'on prend l'HHPG coupé à 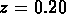 , on voit
que
, on voit
que 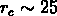
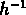 Mpc et
Mpc et 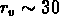
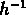 Mpc .
La prévision des modèles est qu'aux petites échelles (
Mpc .
La prévision des modèles est qu'aux petites échelles (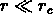 ),
les
),
les 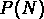 montrent une chute exponentielle. Aux échelles
intermédiaires (
montrent une chute exponentielle. Aux échelles
intermédiaires (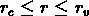 ), on devrait observer la loi
), on devrait observer la loi
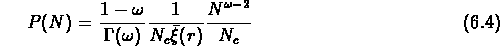
avec une coupure supérieure pour 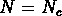 .
Aux grandes échelles (
.
Aux grandes échelles (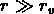 ), on devrait avoir une
loi de puissance avec une coupure inférieure pour
), on devrait avoir une
loi de puissance avec une coupure inférieure pour 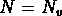 .
Les figures
.
Les figures ![]() et
et ![]() montent que
le comportement des amas semble comparable à celui des galaxies et
reproduise effectivement ces trois comportements.
montent que
le comportement des amas semble comparable à celui des galaxies et
reproduise effectivement ces trois comportements.
Les modèles à invariance d'échelle prévoient aussi l'existence de
deux régimes extrèmes pour les comptages: les cas très denses, quand
 , et très sous-denses, quand
, et très sous-denses, quand  ,
dans lesquels existent des relations d'invariance d'échelle
caractérisées par les fonctions h et g:
,
dans lesquels existent des relations d'invariance d'échelle
caractérisées par les fonctions h et g:
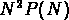 est proportionnel à
est proportionnel à 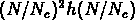 quand
quand
 , N > 1 et
, N > 1 et 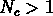 .
.
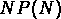 est proportionnel à
est proportionnel à 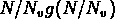 quand
quand 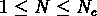 .
La figure
.
La figure ![]() montre la fonction h: il est évident
que les courbes correspondant aux valeurs différentes de N se regroupent,
que le fit qui correspond à
montre la fonction h: il est évident
que les courbes correspondant aux valeurs différentes de N se regroupent,
que le fit qui correspond à
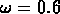 est une bonne approximation pour les
est une bonne approximation pour les 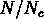 petits et,
surtout, la loi suivie est semblable à celle des galaxies du SSRS
(Maurogordato, Schaeffer & da Costa, 1992).
petits et,
surtout, la loi suivie est semblable à celle des galaxies du SSRS
(Maurogordato, Schaeffer & da Costa, 1992).

Figure: P(N) en fonction de N pour l' échantillon d'amas
HHPG limité à 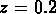

Figure: 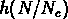 en fonction de
en fonction de 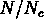 pour l' échantillon d'amas
HHPG limité à
pour l' échantillon d'amas
HHPG limité à 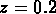
Un autre argument en faveur de ces modèles
est donné par la mesure directe des fonctions de corrélation moyennes
à deux et trois points, 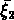 et
et 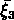 , ou de la
variance
, ou de la
variance 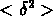 et de la skewness
et de la skewness 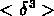 des
comptages, où
des
comptages, où 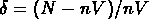 (Cappi & Maurogordato, 1993).
Or, dans le cadre par exemple d'un Univers à invariance d'échelle ,
on a une relation hierarchique entre les fonctions de correlation à
N points, et en particulier:
(Cappi & Maurogordato, 1993).
Or, dans le cadre par exemple d'un Univers à invariance d'échelle ,
on a une relation hierarchique entre les fonctions de correlation à
N points, et en particulier:

On devrait donc avoir la relation 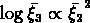 ;
c'est en effet ce que nous
trouvons pour les amas de divers échantillons comme pour les
galaxies CfA et SSRS (voir figure
;
c'est en effet ce que nous
trouvons pour les amas de divers échantillons comme pour les
galaxies CfA et SSRS (voir figure ![]() ), avec
), avec
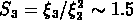 .
.

Figure: 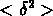 --
-- 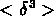 pour différents catalogues de
galaxies et d'amas: CfA40 (asterisques), SSRS40 (cercles), N40
(croix), S40 (carrés)
pour différents catalogues de
galaxies et d'amas: CfA40 (asterisques), SSRS40 (cercles), N40
(croix), S40 (carrés)
Il faut donc conclure que les amas aussi suivent une distribution
à invariance d'échelle . Cela s'inscrit dans le cadre d'un univers où
les structures se forment par clustering gravitationnel.
Dans la théorie de la formation biaisée (Kaiser, 1984)
on peut supposer que la distribution des amas
reflète les mêmes propriétés statistiques que celle des galaxies.
Comme je l'ai mentionné dans le cas du plan fondamental, nous avons plusieurs
indications en faveur d'une origine identique des structures,
poussant l'idée que la gravité est un moteur suffisant pour expliquer
la distribution des structures que nous observons aujourd'hui.
Il reste à clarifier le rôle et la distribution de la matière
sombre ![]() .
.