Star Formation Rate
To build a Composite Stellar Population (CSP) we need the birthrate of
stars. The Star Formation Rate depends on the amount of gas converted in
stars in the galaxy: 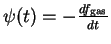 .
The Schmidt's (1959) law assumes that the rate of star formation varies
with a power
.
The Schmidt's (1959) law assumes that the rate of star formation varies
with a power 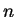 of the density of interstellar gas,
of the density of interstellar gas, 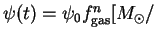 yr],
with
yr],
with 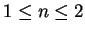 (see also Tinsley 1980). Assuming
(see also Tinsley 1980). Assuming 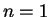 and a closed-box model (constant total mass) with instantaneous recycling
of the gas ejected by the stellar remnants, the Schmidt's law leads to
the analytic approximation
and a closed-box model (constant total mass) with instantaneous recycling
of the gas ejected by the stellar remnants, the Schmidt's law leads to
the analytic approximation 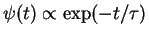 ,
also called
,
also called 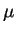 -model,
being
-model,
being 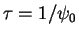 the timescale. The integrated spectrum of a stellar population with an
arbitrary star formation rate
the timescale. The integrated spectrum of a stellar population with an
arbitrary star formation rate 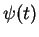 can be obtained from the spectrum of a SSP by means of the convolution
integral:
can be obtained from the spectrum of a SSP by means of the convolution
integral:
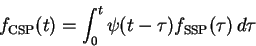
assuming that the IMF does not change with time. To reproduce the
colours of galaxies of different spectral types, we use the parameters
of SFR listed in Table 2: the early
galaxies can be matched by a delta burst or by an exponentially decaying
SFR with 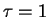 Gyr,
S0 and Spiral galaxies are well reproduced by a Schmidt law with timescales
ranging from 2 and 30Gyr, and the Irregulars can be represented by a constant
SFR.
Gyr,
S0 and Spiral galaxies are well reproduced by a Schmidt law with timescales
ranging from 2 and 30Gyr, and the Irregulars can be represented by a constant
SFR.
Table:Characteristics of the SFR adopted
to match the SEDs of different spectral types of observed galaxies.
| file |
SpT |
SFR |
Timescale |
| ./ZPHOT/templates/Burst.ised |
Burst |
Single Burst |
-- |
| ./ZPHOT/templates/E.ised |
E |
Exponential |
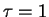 Gyr
Gyr |
| ./ZPHOT/templates/S0.ised |
S0 |
Exponential |
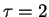 Gyr
Gyr |
| ./ZPHOT/templates/Sa.ised |
Sa |
Exponential |
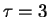 Gyr
Gyr |
| ./ZPHOT/templates/Sb.ised |
Sb |
Exponential |
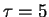 Gyr
Gyr |
| ./ZPHOT/templates/Sc.ised |
Sc |
Exponential |
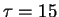 Gyr
Gyr |
| ./ZPHOT/templates/Sd.ised |
Sd |
Exponential |
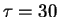 Gyr
Gyr |
| ./ZPHOT/templates/Im.ised |
Im |
Constant |
-- |
|
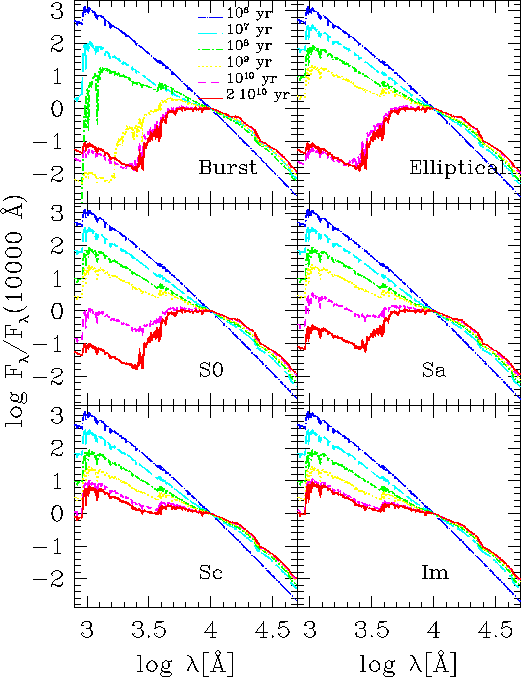 |
Figure:Evolution of the SEDs
of different spectral types computed using the spectral evolutionary models
of Bruzual & Charlot (1993), with Miller & Scalo IMF, solar metallicity
and characteristics of the SFR as shown in Table 1.
In Figure 3 we show the evolution of the
SEDs for 6 of the considered spectral types. The CSP are built with the
GISSEL98 library, with Miller & Scalo IMF, solar metallicity and different
SFRs, as in Table 2. The represented
ages range from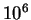 yr
to
yr
to 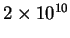 yr:
we can remark that at the younger ages all the SEDs resemble each other,
whereas they start to differentiate at ages
yr:
we can remark that at the younger ages all the SEDs resemble each other,
whereas they start to differentiate at ages  yr,
when the 4000Å break becomes detectable. Moreover it is evident that
the size of the 4000Å break is much more conspicuous for earlier
types.
yr,
when the 4000Å break becomes detectable. Moreover it is evident that
the size of the 4000Å break is much more conspicuous for earlier
types.
micol bolzonella
2000-12-10
![]() Gyr,
S0 and Spiral galaxies are well reproduced by a Schmidt law with timescales
ranging from 2 and 30Gyr, and the Irregulars can be represented by a constant
SFR.
Gyr,
S0 and Spiral galaxies are well reproduced by a Schmidt law with timescales
ranging from 2 and 30Gyr, and the Irregulars can be represented by a constant
SFR.
